الگوریتم دایکسترا

[mohammad1]

در نظریه گراف، الگوریتم دیکسترا یکی از الگوریتم‌های پیمایش گراف است که توسط دانشمند هلندی علوم رایانه، اِدْسْخِر دِیْکْسْترا در سال ۱۹۵۹ ارایه شد.
این الگوریتم یکی از الگوریتم‌های پیمایش گراف است که مسئلهٔ کوتاه‌ترین مسیر از مبدأ واحد را برای گراف‌های وزن‌داری که یال با وزن منفی ندارند، حل می‌کند و در نهایت با ایجاد درخت کوتاه‌ترین مسیر، کوتاه‌ترین مسیر از مبدأ به همهٔ رأس‌های گراف را به دست می‌دهد. همچنین می‌توان از این الگوریتم برای پیدا کردن کوتاه‌ترین مسیر از مبدأ تا رأس مقصد به این ترتیب بهره جست که در حین اجرای الگوریتم به محض پیداشدن کوتاه‌ترین مسیر از مبدأ به مقصد، الگوریتم را متوقف کرد.
الگوریتم دایکسترا به نام کوتاه ترین مسیر تک منبع (single-source shortest path) نیز معروف است و مشابه الگوریتم پریم می باشد در صورتی که گراف یال با وزن منفی داشته باشد، این الگوریتم درست کار نمی‌کند و می‌بایست از الگوریتم‌های دیگر نظیر الگوریتم بلمن-فورد که پیچیدگی زمانی آنها بیشتر است استفاده کنیم.
خط مشی الگوریتم دیکسترا، مشابه با روش حریصانهٔ استفاده شده در الگوریتم پریم برای پیدا کردن زیر درخت فراگیر بهینه است.


[TABLE="class: infobox, width: 22"]
الگوریتم دایکسترا[TR]
[TD="colspan: 2, align: center"]

اجرا الگوریتم دیکسترا[/TD]
[/TR]
[TR]
[TH="align: right"]کلاس[/TH]
[TD]الگوریتم جستجو[/TD]
[/TR]
[TR]
[TH="align: right"]داده ساختار[/TH]
[TD]Graph[/TD]
[/TR]
[TR]
[TH="align: right"]بدترین زمان اجرا[/TH]
[TD]

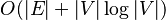[/TD]
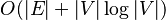
[/TR]
[TR]
[TD="colspan: 2, align: left"]ن • ب • و




[/TD]
[/TR]
[/TABLE]







[TABLE]
[TR]
[TD="class: gutter"]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
[/TD]
[TD="class: code"]//In The Name Of God

static void finder(int start, int end, double mweight, int[] way, int count)

{
count += 1;
for (int i = 1; i <= p; i++)
{
if (weight[start, i] > 0 && weight[i, i] == 0)
{
if (i == end)
{
mweight += weight[start, i];
way[count] = end;


if (mweight < least)
{
least = mweight;
for (int j = 0; j < 20; j++)
bestway[j] = way[j];
}
mweight -= weight[start, i];
continue;
}
mweight += weight[start, i];
weight[start, start] = -1;
way[count] = i;
finder(i, end, mweight, way, count);
way[count + 1] = 0;
weight[start, start] = 0;
mweight -= weight[start, i];
}
}
}
//خروجی این تابع آرایه ی BestWay است
//که کوتاه ترین مسیر درون آن قرار میگیرد.

[/TD]
[/TR]
[/TABLE]