چرخزاد

[goodarz]

نمودار تابع چرخزاد تولید شده توسط یه دایره به شعاع 1 رو در بازه

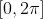در نظر بگیرید و دایره C رو به شعاع 1 در نقطه به طول

روی محور x ها بر این محور و منحنی مماس کنید و نقطه تماس این دایره با منحنی رو R بنامید. فرض کنید P نقطه ای روی منحنی باشه و خط موازی محور x ها که از P رسم میشه دایره C رو برای بار اول در Q قطع کنه. ثابت کنید مماس بر منحنی در نقطه P و پاره خط QR با هم موازیند.

دوستانی که با منحنی چرخزاد آشنایی ندارن میتونن اینجا رو ببینن: Cycloid - Wikipedia, the free encyclopedia

(خواهشا از مشتق و کوفت و ..... استفاده نکنید, راه حل با مشتقش رو خودم بلدم. دنبال یه راه حل هندسی می گردم.)

 

[amir.ekhlasi]

پاسخ : چرخزاد

آخه فضای مماس بر یک منحنی با مشتق تعریف میشه ! (منظورم خط مماسه)

 

[goodarz]

پاسخ : چرخزاد

اونجایی که من ازش این سوالو دیدم گفته بود راه حل هندسی هم داره.

 

[goodarz]

پاسخ : چرخزاد

آخه فضای مماس بر یک منحنی با مشتق تعریف میشه ! (منظورم خط مماسه)

فکر نکنم این چیزی که میگید درست باشه, مثلا برای بیضی میدونیم خط مماس تو یه نقطه نیمساز خارجی زاویه ایه که اون نقطه با دوتا کانون ها می سازه و این اثبات کاملا هندسی هم داره.....

 

[amir.ekhlasi]

پاسخ : چرخزاد

خوب البته برای حالات خاص از جمله دایره و بیضی میشه تعبیر هندسی کرد. یعنی در حالات خاص خط مماس را تعریف کرد. ولی در کل تعریف خط مماس با همون مشتق انجام میشه که در حالات خاص ثابت میشه با تعاریف خاص یکی است. (خودمم نفهمیدم جمله آخرم چیه!!)

 

[amir.ekhlasi]

پاسخ : چرخزاد

اینا ببینیدTangent Vector -- from Wolfram MathWorld

 

[goodarz]

پاسخ : چرخزاد

خوب البته برای حالات خاص از جمله دایره و بیضی میشه تعبیر هندسی کرد. یعنی در حالات خاص خط مماس را تعریف کرد. ولی در کل تعریف خط مماس با همون مشتق انجام میشه که در حالات خاص ثابت میشه با تعاریف خاص یکی است. (خودمم نفهمیدم جمله آخرم چیه!!)

حوب مگه من چی میگم؟؟ منم میگم بعضی از منحنی ها هستن که میشه خط مماس بر اونا رو به طور هندسی هم تعریف کرد......