دو تیم
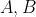با تعداد اعضای متفاوت در یک مسابقه ی پینگ پنگ به این شکل بازی می کنند:
فقط یک میز برای بازی وجود دارد و دو بازیکن از دو تیم مختلف با هم بازی می کنند و بقیه ی بازیکنان یک صف تشکیل می دهند. بعد از هر بازی نفر اول صف جایگزین هم تیمی خودش می شود و بازیکن قبلی به آخر صف می رود. ثابت کنید هر دو بازیکنی که از دو تیم متفاوت انتخاب کنیم حتما با هم بازی خواهند کرد.
فقط یک میز برای بازی وجود دارد و دو بازیکن از دو تیم مختلف با هم بازی می کنند و بقیه ی بازیکنان یک صف تشکیل می دهند. بعد از هر بازی نفر اول صف جایگزین هم تیمی خودش می شود و بازیکن قبلی به آخر صف می رود. ثابت کنید هر دو بازیکنی که از دو تیم متفاوت انتخاب کنیم حتما با هم بازی خواهند کرد.
