خطی که ارتفاع را نصف می کند
پاسخ : خطی که ارتفاع را نصف می کند
منلائوس سوال رو می ترکونه.
@mathh:
سوال توی تالار هندسه ی ممتاز مطرح شده، یعنی راه حلی که مدنظر ایشون بوده، ساده نبوده. تازه اگر هم مشکلی بود، باید در پیغام شخصی مطرح می کردید.
مثلث
 را با ارتفاع های
را با ارتفاع های
 در نظر بگیرید.
در نظر بگیرید.
 یکدیگر را در
یکدیگر را در
 قطع می کنند(
قطع می کنند(
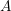 بین
بین
 ). همچنین
). همچنین
 طوری روی
طوری روی
 انتخاب شده که
انتخاب شده که
 . ثابت کنید
. ثابت کنید
 از وسط ارتفاع
از وسط ارتفاع
 می گذرد.
می گذرد.
@mathh:
سوال توی تالار هندسه ی ممتاز مطرح شده، یعنی راه حلی که مدنظر ایشون بوده، ساده نبوده. تازه اگر هم مشکلی بود، باید در پیغام شخصی مطرح می کردید.
آخرین ویرایش توسط مدیر
پاسخ : خطی که ارتفاع را نصف می کند
این هم لینک منبع: AoPS Forum - middle of altitude • Art of Problem Solving
از همساز استفاده ی خوبی کرده.
این هم لینک منبع: AoPS Forum - middle of altitude • Art of Problem Solving
از همساز استفاده ی خوبی کرده.
پاسخ : خطی که ارتفاع را نصف می کند
با سلام
من با اطلاعات مقدماتی حلش کردم
اگه محل بر خورد mkبا cf رو nبگیرید میخواهیم ثابت کنیم که sin ckn/sin fkn=kf/kc
تو خط سوم اثبات توجه کنید که از این نکته که MEC=ABE , MED = EBC استفاده کردیم.
پس لازم نیست کل خوشخوان رو خونده باشیم! دو سه تا فصل اول هم میتونه کافی باشه!
امتیاز یادتون نره!
با تشکر
ماهان بابلیان
با سلام
من با اطلاعات مقدماتی حلش کردم
اگه محل بر خورد mkبا cf رو nبگیرید میخواهیم ثابت کنیم که sin ckn/sin fkn=kf/kc
SIN CKM / SIN DKM = MC/MD.KD/KC
پس باید ثابت کنیم : MC/MD . KD/KC = KF/KCیعنی MC/MD = KF/KD
KF/KD = SIN KCF/SIN KCD.CF/CD = AF/AB . BC/CF. CF/CD=AF/AB.BC/CD
یعنی حکم جدید میشه AF/AB . BC/CD= MC/MD
MC/MD = SIN ABE /SIN EBC . EC/ED= (AE/AB)/(EC/BC).EC/ED = BC.AE.EC/AB.EC.ED=BC.AE/AB.ED
حالا با توجه به حکم بالا باید ثابت کنیم AF/AB . BC/CD = BC.AE/AB.ED که این هم به خاطر تشابه دو مثلث AFE , DCE بدیهیه!
تو خط سوم اثبات توجه کنید که از این نکته که MEC=ABE , MED = EBC استفاده کردیم.
پس لازم نیست کل خوشخوان رو خونده باشیم! دو سه تا فصل اول هم میتونه کافی باشه!
امتیاز یادتون نره!
با تشکر
ماهان بابلیان
