حرکت پرتابه ای روی سطح شیبدار
پاسخ : حرکت پرتابه ای روی سطح شیبدار
سلام جواب آخری که بدست آوردم اینه :

معادلات رو نوشتم ، از X نسبت به تتا مشتق گرفتم ، مساوی صفر قرار دادم ، یه ذره اتحاد مثلثاتی زدم ، به این رابطه رسیدم که بعد arc میگیریم تتا بدست میاد
البته مطمئن نیستم ولی هرچی چک میکنم فک نکنم اشتباه باشه !
سلام جواب آخری که بدست آوردم اینه :
معادلات رو نوشتم ، از X نسبت به تتا مشتق گرفتم ، مساوی صفر قرار دادم ، یه ذره اتحاد مثلثاتی زدم ، به این رابطه رسیدم که بعد arc میگیریم تتا بدست میاد
البته مطمئن نیستم ولی هرچی چک میکنم فک نکنم اشتباه باشه !
آخرین ویرایش توسط مدیر
پاسخ : حرکت پرتابه ای روی سطح شیبدار
با دو روش ميشه حل کرد ، در واقع دو مختصات مختلف:
1) ميشه محورهای مختصات را به طور معمولی افقی و عمودی در نظر گرفت و معادلات رو نوشت، در نهايت معادله مسير بدست مياد . مختصات نقطه B بايد در معادله مسير صدق کنه.
دقت کنيد که در معادلات مسير زاويه تتا دخيل هست و در مختصات نقطه B زاويه فی !
2) ميشه محور x را موازی با سطح و محور y را عمود بر سطح شيبدار در نظر گرفت. توجه کنيد که در اين حالت شتاب گرنی هم بايد تجزيه بشه و معادلات در دو مختصه نوشته بشه !
هر وقت در معادله y ، مقدار ان برابر صفر باشد ، دو جواب برای t بدست مياد . که يکی مربوط به لحظه پرتاب هست و ديگری مربوط به زمانی که ميرسه به نقطه B .
با قرار دادن t در معادله x ميشه فاصله نقاط A تا B رو بدست اورد.
جواب نهايی برای حداکثر شدن برد پرتابه : (Pi/4)-(Fi/2)
(مسئله آخر فصل اول مکانيک کلپنر)
با دو روش ميشه حل کرد ، در واقع دو مختصات مختلف:
1) ميشه محورهای مختصات را به طور معمولی افقی و عمودی در نظر گرفت و معادلات رو نوشت، در نهايت معادله مسير بدست مياد . مختصات نقطه B بايد در معادله مسير صدق کنه.
دقت کنيد که در معادلات مسير زاويه تتا دخيل هست و در مختصات نقطه B زاويه فی !
2) ميشه محور x را موازی با سطح و محور y را عمود بر سطح شيبدار در نظر گرفت. توجه کنيد که در اين حالت شتاب گرنی هم بايد تجزيه بشه و معادلات در دو مختصه نوشته بشه !
هر وقت در معادله y ، مقدار ان برابر صفر باشد ، دو جواب برای t بدست مياد . که يکی مربوط به لحظه پرتاب هست و ديگری مربوط به زمانی که ميرسه به نقطه B .
با قرار دادن t در معادله x ميشه فاصله نقاط A تا B رو بدست اورد.
جواب نهايی برای حداکثر شدن برد پرتابه : (Pi/4)-(Fi/2)
(مسئله آخر فصل اول مکانيک کلپنر)
پاسخ : حرکت پرتابه ای روی سطح شیبدار
ببین دوست عزیز یبن aوb جابجایی در راستای عمود بر سطح صفره.....پس با نوشتن روابط(دقت کن باید بنویسی(g*cos(phiنه g تنها)زمان بدست یاد
این زمان رو در معادله حرکت در راستای موازی با سطح جایگذاری کنی(اینجا حرکت شتاب داره و شتاب برابر هست با(g*sin(phi) یه رابطه بدست میاد که همون اندازه AB هست
ک ازش نسبت به تتا مشتق بگیرید مساوی صفر قرار بدید حله و میشه اونی که نوشتم:3:
میشه یه نفرتون راه حلتونو بگید ؟
این زمان رو در معادله حرکت در راستای موازی با سطح جایگذاری کنی(اینجا حرکت شتاب داره و شتاب برابر هست با(g*sin(phi) یه رابطه بدست میاد که همون اندازه AB هست
ک ازش نسبت به تتا مشتق بگیرید مساوی صفر قرار بدید حله و میشه اونی که نوشتم:3:
پاسخ : حرکت پرتابه ای روی سطح شیبدار
شکل جواب ساده تر از اين حرفهاست. فبل از اينکه مشتق بگيری، سعی کن جواب رو به ساده ترين شکل در بياری
اونوقت بعدش اصلا مشتق هم لازم نميشه !
ببین دوست عزیز یبن aوb جابجایی در راستای عمود بر سطح صفره.....پس با نوشتن روابط(دقت کن باید بنویسی(g*cos(phiنه g تنها)زمان بدست یاد
این زمان رو در معادله حرکت در راستای موازی با سطح جایگذاری کنی(اینجا حرکت شتاب داره و شتاب برابر هست با(g*sin(phi) یه رابطه بدست میاد که همون اندازه AB هست
ک ازش نسبت به تتا مشتق بگیرید مساوی صفر قرار بدید حله و میشه اونی که نوشتم:3:
این زمان رو در معادله حرکت در راستای موازی با سطح جایگذاری کنی(اینجا حرکت شتاب داره و شتاب برابر هست با(g*sin(phi) یه رابطه بدست میاد که همون اندازه AB هست
ک ازش نسبت به تتا مشتق بگیرید مساوی صفر قرار بدید حله و میشه اونی که نوشتم:3:
اونوقت بعدش اصلا مشتق هم لازم نميشه !
پاسخ : حرکت پرتابه ای روی سطح شیبدار
من کلاً کلپنر رو هنوز بازش نکردم ولی الآن رفتم و دیدم سوال آخر فصل یکش رو ، دیدم درست میگید
جواب حالت خاصی رو هم که خود کلپنر گفته ، گذاشتم جای جواب خودم و درست دراومد
من از راه دومی که گفتید رفتم و معادلات رو بدست آوردم
مطمئنید مشتق نمیخواد ؟ یه مشتق خوفی هم گرفتم و اتحاد مثلثاتی هم زدم
از این سینوس و کسینوس و تانژانت آلفا به اضافه بتا استفاده کردم و فکر کنم باید استفاده شه
مگر اینکه ایده بزنی ! که من از راه بیل زنیش رفتم :دی
با دو روش ميشه حل کرد ، در واقع دو مختصات مختلف:
1) ميشه محورهای مختصات را به طور معمولی افقی و عمودی در نظر گرفت و معادلات رو نوشت، در نهايت معادله مسير بدست مياد . مختصات نقطه B بايد در معادله مسير صدق کنه.
دقت کنيد که در معادلات مسير زاويه تتا دخيل هست و در مختصات نقطه B زاويه فی !
2) ميشه محور x را موازی با سطح و محور y را عمود بر سطح شيبدار در نظر گرفت. توجه کنيد که در اين حالت شتاب گرنی هم بايد تجزيه بشه و معادلات در دو مختصه نوشته بشه !
هر وقت در معادله y ، مقدار ان برابر صفر باشد ، دو جواب برای t بدست مياد . که يکی مربوط به لحظه پرتاب هست و ديگری مربوط به زمانی که ميرسه به نقطه B .
با قرار دادن t در معادله x ميشه فاصله نقاط A تا B رو بدست اورد.
جواب نهايی برای حداکثر شدن برد پرتابه : (Pi/4)-(Fi/2)
(مسئله آخر فصل اول مکانيک کلپنر)
1) ميشه محورهای مختصات را به طور معمولی افقی و عمودی در نظر گرفت و معادلات رو نوشت، در نهايت معادله مسير بدست مياد . مختصات نقطه B بايد در معادله مسير صدق کنه.
دقت کنيد که در معادلات مسير زاويه تتا دخيل هست و در مختصات نقطه B زاويه فی !
2) ميشه محور x را موازی با سطح و محور y را عمود بر سطح شيبدار در نظر گرفت. توجه کنيد که در اين حالت شتاب گرنی هم بايد تجزيه بشه و معادلات در دو مختصه نوشته بشه !
هر وقت در معادله y ، مقدار ان برابر صفر باشد ، دو جواب برای t بدست مياد . که يکی مربوط به لحظه پرتاب هست و ديگری مربوط به زمانی که ميرسه به نقطه B .
با قرار دادن t در معادله x ميشه فاصله نقاط A تا B رو بدست اورد.
جواب نهايی برای حداکثر شدن برد پرتابه : (Pi/4)-(Fi/2)
(مسئله آخر فصل اول مکانيک کلپنر)
جواب حالت خاصی رو هم که خود کلپنر گفته ، گذاشتم جای جواب خودم و درست دراومد
من از راه دومی که گفتید رفتم و معادلات رو بدست آوردم
مطمئنید مشتق نمیخواد ؟ یه مشتق خوفی هم گرفتم و اتحاد مثلثاتی هم زدم
از این سینوس و کسینوس و تانژانت آلفا به اضافه بتا استفاده کردم و فکر کنم باید استفاده شه
مگر اینکه ایده بزنی ! که من از راه بیل زنیش رفتم :دی
پاسخ : حرکت پرتابه ای روی سطح شیبدار
خب استاد من هم همینو بدست آوردم دیگه فردا راهمو کامل میزارم بقیه هم ببینن
با دو روش ميشه حل کرد ، در واقع دو مختصات مختلف:1) ميشه محورهای مختصات را به طور معمولی افقی و عمودی در نظر گرفت و معادلات رو نوشت، در نهايت معادله مسير بدست مياد . مختصات نقطه B بايد در معادله مسير صدق کنه.دقت کنيد که در معادلات مسير زاويه تتا دخيل هست و در مختصات نقطه B زاويه فی !2) ميشه محور x را موازی با سطح و محور y را عمود بر سطح شيبدار در نظر گرفت. توجه کنيد که در اين حالت شتاب گرنی هم بايد تجزيه بشه و معادلات در دو مختصه نوشته بشه !هر وقت در معادله y ، مقدار ان برابر صفر باشد ، دو جواب برای t بدست مياد . که يکی مربوط به لحظه پرتاب هست و ديگری مربوط به زمانی که ميرسه به نقطه B .با قرار دادن t در معادله x ميشه فاصله نقاط A تا B رو بدست اورد.جواب نهايی برای حداکثر شدن برد پرتابه : (Pi/4)-(Fi/2)(مسئله آخر فصل اول مکانيک کلپنر)
پاسخ : حرکت پرتابه ای روی سطح شیبدار
سلام
در رابطه شما به جای فی بايد فی دوم باشه !
جواب برد به شکل زير هست !
با توجه به اينکه متغير زاويه تتا هست ، پس عبارت سينوس دوم بايد حداکثر باشه (برابر يک) .
پس حاصل عبارت داخل پرانتز دومی بايد پی دوم باشه . با مشتق هم به همين نتيجه میرسيد .
مشاهده پیوست 205
بله یه لحظه توی مشتق گرفتن اشتباه کرده بودم
الآن بدست آوردم :

که حالت خاص فی مساوی صفر هم جواب میده.
البته شاید صورت و مخرج برعکس باشن
الآن بدست آوردم :
که حالت خاص فی مساوی صفر هم جواب میده.
البته شاید صورت و مخرج برعکس باشن
در رابطه شما به جای فی بايد فی دوم باشه !
جواب برد به شکل زير هست !
با توجه به اينکه متغير زاويه تتا هست ، پس عبارت سينوس دوم بايد حداکثر باشه (برابر يک) .
پس حاصل عبارت داخل پرانتز دومی بايد پی دوم باشه . با مشتق هم به همين نتيجه میرسيد .
مشاهده پیوست 205
پاسخ : حرکت پرتابه ای روی سطح شیبدار
دو مسئله راجع به برد پرتابه :
1) فرض کنيد جسمی را با سرعت اوليه V[SUB]0[/SUB] از بالای صخره ای به ارتفاع h با زاويه تتا پرتاب می کنيم.
فاصله افقی محل برخورد جسم با سطح زمين تا محل پرتاب را برد s می ناميم.
حداکثر برد پرتابه چقدر است و در چه زاويه ای بدست می آيد؟ شکل 1
(بدون مشتق گيری هم حل می شود !!! )
حالا ميشه برای سخت تر کردن مسئله، مسئله بالا و مسئله سطح شيبدار رو باهم ترکيب کرد !
2) فرض کنيد جسمی را با سرعت اوليه V[SUB]0[/SUB] از بالای صخره ای به ارتفاع h با زاويه تتا پرتاب می کنيم.
محل پرتاب در قسمت بالای تپه ای با شيب فی قرار دارد.
فاصله محل برخورد جسم با سطح تپه را تا پای محل پرتاب را برد R می ناميم.
حداکثر برد پرتابه چقدر است و در چه زاويه ای بدست می آيد؟ شکل 2
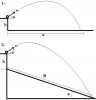
دو مسئله راجع به برد پرتابه :
1) فرض کنيد جسمی را با سرعت اوليه V[SUB]0[/SUB] از بالای صخره ای به ارتفاع h با زاويه تتا پرتاب می کنيم.
فاصله افقی محل برخورد جسم با سطح زمين تا محل پرتاب را برد s می ناميم.
حداکثر برد پرتابه چقدر است و در چه زاويه ای بدست می آيد؟ شکل 1
(بدون مشتق گيری هم حل می شود !!! )
حالا ميشه برای سخت تر کردن مسئله، مسئله بالا و مسئله سطح شيبدار رو باهم ترکيب کرد !
2) فرض کنيد جسمی را با سرعت اوليه V[SUB]0[/SUB] از بالای صخره ای به ارتفاع h با زاويه تتا پرتاب می کنيم.
محل پرتاب در قسمت بالای تپه ای با شيب فی قرار دارد.
فاصله محل برخورد جسم با سطح تپه را تا پای محل پرتاب را برد R می ناميم.
حداکثر برد پرتابه چقدر است و در چه زاويه ای بدست می آيد؟ شکل 2

پاسخ : حرکت پرتابه ای روی سطح شیبدار
با عرض معذرت، این معادله ی توی نقل قول رو نمیدونم درسته یا نه ولی به نظرم دارید اشتباه میکنید
من راه حلم رو مینویسم ، شاید هم من دارم اشتباه میکنم
اون موقع بهم بگید
آخه توی جوابم اگه حالت خاص فی مساوی صفر و فی مساوی 60 که خود کلپنر هم گذاشته جواب میده
حالا راه رو مینویسم خودتون بگین کجاش غلطه
دستگاه مختصات رو در راستای حرکت پرتابه گرفتم :

معادله ی x رو هم بنویسیم ، با توجه به دستگاه مختصاتمون ، توی راستای ایکس هم شتاب خواهیم داشت و معادلمون با جایگذاری T اینطوری میشه :

بعد از x نسبت به تتا مشتق میگیریم ، و مساوی صفر میذاریم

در نتیجه با ساده کردن و اضافه کردن یک جمله برای ایجاد اتحاد سینوس دو به اضافه کسینوس دو = 1خواهیم داشت

سمت راست برابر کسینوس 2 تتا + 2فی و سمت چپ پرابر سینوس 2 تتا + 2فی ضربدر تانژانت فی
در نتیجه یک بار دیگه هم اشتباه کردم !
جوابم شد :

اگه قرار بدیم فی مساوی صفر ، تانژانت فی مساوی با صفر ، میشه صفر و کتانژانت دو تتا هم باید بشه صفر پس تتا باید بشه پی چهارم
و به اضای فی مساوی 60 ، مثال خود کلپنر ، جواب تتا در میاد 15
دیگه این درسته
اگه اتحاد مثلثاتی هم بزنیم ، میشه مقدار تتا رو برحسب فی بدست آورد
سلام
در رابطه شما به جای فی بايد فی دوم باشه !
جواب برد به شکل زير هست !
با توجه به اينکه متغير زاويه تتا هست ، پس عبارت سينوس دوم بايد حداکثر باشه (برابر يک) .
پس حاصل عبارت داخل پرانتز دومی بايد پی دوم باشه . با مشتق هم به همين نتيجه میرسيد .
مشاهده پیوست 205
در رابطه شما به جای فی بايد فی دوم باشه !
جواب برد به شکل زير هست !
با توجه به اينکه متغير زاويه تتا هست ، پس عبارت سينوس دوم بايد حداکثر باشه (برابر يک) .
پس حاصل عبارت داخل پرانتز دومی بايد پی دوم باشه . با مشتق هم به همين نتيجه میرسيد .
مشاهده پیوست 205
من راه حلم رو مینویسم ، شاید هم من دارم اشتباه میکنم
اون موقع بهم بگید
آخه توی جوابم اگه حالت خاص فی مساوی صفر و فی مساوی 60 که خود کلپنر هم گذاشته جواب میده
حالا راه رو مینویسم خودتون بگین کجاش غلطه
دستگاه مختصات رو در راستای حرکت پرتابه گرفتم :
معادله ی x رو هم بنویسیم ، با توجه به دستگاه مختصاتمون ، توی راستای ایکس هم شتاب خواهیم داشت و معادلمون با جایگذاری T اینطوری میشه :
بعد از x نسبت به تتا مشتق میگیریم ، و مساوی صفر میذاریم
در نتیجه با ساده کردن و اضافه کردن یک جمله برای ایجاد اتحاد سینوس دو به اضافه کسینوس دو = 1خواهیم داشت
سمت راست برابر کسینوس 2 تتا + 2فی و سمت چپ پرابر سینوس 2 تتا + 2فی ضربدر تانژانت فی
در نتیجه یک بار دیگه هم اشتباه کردم !
جوابم شد :
اگه قرار بدیم فی مساوی صفر ، تانژانت فی مساوی با صفر ، میشه صفر و کتانژانت دو تتا هم باید بشه صفر پس تتا باید بشه پی چهارم
و به اضای فی مساوی 60 ، مثال خود کلپنر ، جواب تتا در میاد 15
دیگه این درسته
اگه اتحاد مثلثاتی هم بزنیم ، میشه مقدار تتا رو برحسب فی بدست آورد
پاسخ : حرکت پرتابه ای روی سطح شیبدار
با روش شما : مقدار x که بدست اورديد را اگه کمی ساده تر کنيد (فاکتور گيری . مخرج مشترک و اتحاد مثلثاتی) به جواب زير میرسيد :
(هميشه قبل از مشتق گيری حتماً جواب رو ساده بکنيد. دکتر خرمی عمراً به جواب ساده نشده نمره بده ! بنده خودم تجربه کردم ! )
مشاهده پیوست 207
با عرض معذرت، این معادله ی توی نقل قول رو نمیدونم درسته یا نه ولی به نظرم دارید اشتباه میکنید
من راه حلم رو مینویسم ، شاید هم من دارم اشتباه میکنم
اون موقع بهم بگید
آخه توی جوابم اگه حالت خاص فی مساوی صفر و فی مساوی 60 که خود کلپنر هم گذاشته جواب میده
حالا راه رو مینویسم خودتون بگین کجاش غلطه
دستگاه مختصات رو در راستای حرکت پرتابه گرفتم :
t \Rightarrow t = \frac{2v_0 sin (\theta + \varphi)}{gcos\varphi})
معادله ی x رو هم بنویسیم ، با توجه به دستگاه مختصاتمون ، توی راستای ایکس هم شتاب خواهیم داشت و معادلمون با جایگذاری T اینطوری میشه :
4v_0 ^2 sin^2(\theta+\varphi)}{2g^2cos^2\varphi}+\frac{2v_0^2 cos(\theta+\varphi)sin(\theta+\varphi)}{gcos\varphi})
بعد از x نسبت به تتا مشتق میگیریم ، و مساوی صفر میذاریم
}{gcos\varphi }=\frac{-2v_0^2 sin^2(\theta+\varphi)+2v_0^2cos^2(\theta+\varphi)}{gcos\varphi})
در نتیجه با ساده کردن و اضافه کردن یک جمله برای ایجاد اتحاد سینوس دو به اضافه کسینوس دو = 1خواهیم داشت
cos(\theta+\varphi)=1-2sin^2(\theta+\varphi))
سمت راست برابر کسینوس 2 تتا + 2فی و سمت چپ پرابر سینوس 2 تتا + 2فی ضربدر تانژانت فی
در نتیجه یک بار دیگه هم اشتباه کردم !
جوابم شد :
=tan \varphi sin 2(\theta + \varphi)\Rightarrow cot 2(\theta + \varphi)=tan \varphi)
اگه قرار بدیم فی مساوی صفر ، تانژانت فی مساوی با صفر ، میشه صفر و کتانژانت دو تتا هم باید بشه صفر پس تتا باید بشه پی چهارم
و به اضای فی مساوی 60 ، مثال خود کلپنر ، جواب تتا در میاد 15
دیگه این درسته
اگه اتحاد مثلثاتی هم بزنیم ، میشه مقدار تتا رو برحسب فی بدست آورد
من راه حلم رو مینویسم ، شاید هم من دارم اشتباه میکنم
اون موقع بهم بگید
آخه توی جوابم اگه حالت خاص فی مساوی صفر و فی مساوی 60 که خود کلپنر هم گذاشته جواب میده
حالا راه رو مینویسم خودتون بگین کجاش غلطه
دستگاه مختصات رو در راستای حرکت پرتابه گرفتم :
معادله ی x رو هم بنویسیم ، با توجه به دستگاه مختصاتمون ، توی راستای ایکس هم شتاب خواهیم داشت و معادلمون با جایگذاری T اینطوری میشه :
بعد از x نسبت به تتا مشتق میگیریم ، و مساوی صفر میذاریم
در نتیجه با ساده کردن و اضافه کردن یک جمله برای ایجاد اتحاد سینوس دو به اضافه کسینوس دو = 1خواهیم داشت
سمت راست برابر کسینوس 2 تتا + 2فی و سمت چپ پرابر سینوس 2 تتا + 2فی ضربدر تانژانت فی
در نتیجه یک بار دیگه هم اشتباه کردم !
جوابم شد :
اگه قرار بدیم فی مساوی صفر ، تانژانت فی مساوی با صفر ، میشه صفر و کتانژانت دو تتا هم باید بشه صفر پس تتا باید بشه پی چهارم
و به اضای فی مساوی 60 ، مثال خود کلپنر ، جواب تتا در میاد 15
دیگه این درسته
اگه اتحاد مثلثاتی هم بزنیم ، میشه مقدار تتا رو برحسب فی بدست آورد
(هميشه قبل از مشتق گيری حتماً جواب رو ساده بکنيد. دکتر خرمی عمراً به جواب ساده نشده نمره بده ! بنده خودم تجربه کردم ! )
مشاهده پیوست 207

