مسابقه ریاضی ((حل کنید !))

[smh-s.salehi]

پاسخ : مسابقه ریاضی ((حل کنید !))

سوال خم و متوازی الاضلاع بدون هیچ قضیه خاصی حل میشه ! فقط یک ایده ساده ساده بزنید!

 

[ash1374]

پاسخ : مسابقه ریاضی ((حل کنید !))

سلام

دو خط l1و l2 موازی محور y ها که خم را قطع می کنن ولی بر آن مماس نیستند رو بگیرید. خم روی این دو خط تعدادی پاره خط به وجود می آورد که کاملا درون خم قرار دارن.بدون کم شدن از جامعیت اثبات، فرض

کنید l1 سمت راست l2 باشد. حالا بالاترین پاره خطی که روی l1 بوجود میاد رو AB بنامید. که A بالاتر از B هست. حالا بالاترین پاره خطی که روی l2 توسط خم بوجود میاد رو DC بگیرید که d بالاتر از C هست.

اگر AB=CD اثبات تمامه. وگرنه فرض کنید AB>CD

اگر نقطه ی Xرو خم باشه تعریف کنید F(X)=X+D-C واضحه F(X نقطه ای در صفحه است که DCXF(X یک متوازی الاضلاعه. حالا X رو از نقطه ی D تا B جابه جا(روی خم) کنید. F(D کاملا بیرون خم و F(B کاملا

درون خم هستند. چون F پیوسته است و جایی بیرون خم و جایی درون خمه پس حتما از D تا B جایی نمودار خم رو قطع میکنه. مثل F(Y پس DCYF(Y متوازی الاضلاعه.

پی نوشت: تابع F همون انتقال طی بردار CD(فرض کنید بالاش علامته برداره:4

 

[Yousefi]

پاسخ : مسابقه ریاضی ((حل کنید !))

من میگم حالا :4:
[299/7]
-[299/21]
+[299/3]
-[299/21]

نه خیر اشتباهه ، شما 2 بار عبارت رو از [299/21] کم کردید ! در صورتی که باید یکبار کم کنید :98:

 

[Yousefi]

پاسخ : مسابقه ریاضی ((حل کنید !))

حالا شما برای ما قضیه خم جردن رو اثبات کن تا ما اینو اثبات کنیم !
اینقدر بدم میاد از این توپولوژی !

 

[smh-s.salehi]

پاسخ : مسابقه ریاضی ((حل کنید !))

سلام
خیلی پیچیده نوشته بودی ولی فکر کنم درست بود
خلاصه اش می شه این که دو مماس موازی از بالا و پایین به خم رسم می کنیم و بعد خط پایین را گرفته و بالا می کشیم تا روی آن یکی بیفتد اگر مقداری از طول پاره خط را که هنگام حرکت درون خم می افتد را x بنامیم آن وقت مقدار x قبل و بعد حرکت صفر است و مقدار آن به صورت پیوسته تغییر می کرده . پس به راحتی می توان گفت مقدار آن در دوجا برابر بوده که آن دوجا دو ضلع متوازی الاضلاع هستند.

 

[ash1374]

پاسخ : مسابقه ریاضی ((حل کنید !))

سلام
خیلی پیچیده نوشته بودی ولی فکر کنم درست بود
خلاصه اش می شه این که دو مماس موازی از بالا و پایین به خم رسم می کنیم و بعد خط پایین را گرفته و بالا می کشیم تا روی آن یکی بیفتد اگر مقداری از طول پاره خط را که هنگام حرکت درون خم می افتد را x بنامیم آن وقت مقدار x قبل و بعد حرکت صفر است و مقدار آن به صورت پیوسته تغییر می کرده . پس به راحتی می توان گفت مقدار آن در دوجا برابر بوده که آن دوجا دو ضلع متوازی الاضلاع هستند.

این چیزی که پیوسته تغییر می کنه مجموع طول پاره خط هایی هست که داخل خم میفتند. یعنی یک خم ممکنه چند تا پاره خط روی یک خط جدا کنه. اگه فقط یکی از این پاره خط ها رو هم در نظر بگیری دیگه پیوسته نیست تغیراتش. البته این مشکل رو میشه حل کرد یعنی کافیه یکم بهتر خط رو حرکت بدی . ولی خوب لازمه دقیق تر بنویسی.

 

[smh-s.salehi]

پاسخ : مسابقه ریاضی ((حل کنید !))

سلام دوباره
اولا این که لطفا دوستان یک کم فعالتر باشند و این جا بیشتر سوال بزارند(مخصوصا کسایی که خودشون سوالا رو حل می کنن!)
در ضمن اینم سوال بعدی سطح حدودا مرحله دوی خوب!)
nنقطی آبی وn نقطه ی قرمز داریم که هیچ سه تایی هم خط نیستند.ثابت کنید می توانیم هر نقطه ی آبی را به یک نقطه ی قرمز طوری وصل کنیم که n پاره خط کشیده شده هیچ نقطه ی تقاطعی نداشته باشند.
:97::97::97::97::97::97::97::97::97:

 

[ash1374]

پاسخ : مسابقه ریاضی ((حل کنید !))

سلام

از اونجایی که تعداد راه های وصل کردن n نقطه ی قرمز به n نقطه ی آبی متناهیه، پس یه حالت مینمم(یا چند تا) داره. یعنی حالتی رو بگیرید که جمع طول همه ی پاره خط ها مینمم باشه. در این حالت اگه AوB

آبی و CوD قرمز باشن و ACوBD متقاطع باشند اگه این دو پاره خط رو با ADوBC جابه جا کنیم به وضوح به حالتی میرسیم که مجموع طول پاره خط ها کمتره و این تناقضه . لذا این حالت مینمم همونیه که مسئله

میخواد.

اگر راه حلم اشکالی نداره سوال بعدی رو بذارم.

 

[math]

پاسخ : مسابقه ریاضی ((حل کنید !))

سلام

از اونجایی که تعداد راه های وصل کردن n نقطه ی قرمز به n نقطه ی آبی متناهیه، پس یه حالت مینمم(یا چند تا) داره. یعنی حالتی رو بگیرید که جمع طول همه ی پاره خط ها مینمم باشه. در این حالت اگه AوB

آبی و CوD قرمز باشن و ACوBD متقاطع باشند اگه این دو پاره خط رو با ADوBC جابه جا کنیم به وضوح به حالتی میرسیم که مجموع طول پاره خط ها کمتره و این تناقضه . لذا این حالت مینمم همونیه که مسئله

میخواد.

اگر راه حلم اشکالی نداره سوال بعدی رو بذارم.

درسته فکر میکنم :53:

فوق العاده قشنگ بود :77::77::77:

 

[ash1374]

پاسخ : مسابقه ریاضی ((حل کنید !))

یه سوال تقریبا معروف اما آموزنده:

چهارضلعی abcd محاطی است. ثابت کنید دوایر نه نقطه ی مثلث های abc,bcd,cda,dab از یک نقطه می گذرند.

 

[Aref]

پاسخ : مسابقه ریاضی ((حل کنید !))

یه سوال تقریبا معروف اما آموزنده:

چهارضلعی abcd محاطی است. ثابت کنید دوایر نه نقطه ی مثلث های abc,bcd,cda,dab از یک نقطه می گذرند.

توی شاریگین هستش. زاویه بازی و خرکاری می خواد فقط.

 

[ash1374]

پاسخ : مسابقه ریاضی ((حل کنید !))

بله تو شاریگین هست.سوال معروفیه. راه حل خوب هم داره.هدفم از مطرح کردن این سوال در واقع مطرح کردن لمی هست که تو این مسائل خیلی بدرد می خوره. قبلش هم باید بچه ها فکر کنن شاید با یه راه خوبی حل کردن. همین خرکاری و زاویه بازی ها هم خودش مهمه.

 

[alimohammadi]

پاسخ : مسابقه ریاضی ((حل کنید !))

یه سوال تقریبا معروف اما آموزنده:

چهارضلعی abcd محاطی است. ثابت کنید دوایر نه نقطه ی مثلث های abc,bcd,cda,dab از یک نقطه می گذرند.

با عرض شرمندگي حوصله ندارم راه دقيق رو بنويسم...
محل برخورد دو تا دايره نه نقطه روM در نظر مي گيريم ثابت ميكنيم(چهارضلعي آبي)GNMJ محاطيه ....
زاويه هاي برابر همرنگ هستند و نقاط مشكي وسط اضلاع.

(در اخر زاويه GMJبرابر زاويه قرمز منهاي زرد شده كه همون زاويه سبز هست ... پس GNMJ محاطيه)

ثابت شد سه دايره‌ي نه نقطه‌ي cdb,edb,ebc همرسند... همينطوري ميشه ثابت كرد 4امين دايره هم از نقطه M ميگذره

 

[ash1374]

پاسخ : مسابقه ریاضی ((حل کنید !))

کاملا درسته.
اگر از وسط هر ضلع چهارضلعی محاطی بر ضلع روبروش عمود کنیم این چهار تا عمود ها هم همرسند.

اگر از هر راس چهار ضلعی محاطی به مرکز ارتفاعی مثلث رو بروش وصل کنیم این چهار خط هم همرسند.

برای حل این مسئله از هر کدوم از لم های بالا هم میشه استفاده کرد. در واقع نقطه ی همرسی دایره نه نقطه ها و نقطه ی همرسی تو سوالای بالا همگی یکی هستند که به این نقطه پادمرکز چهارضلعی محاطی می گن و خواص زیادی داره.

 

[math]

پاسخ : مسابقه ریاضی ((حل کنید !))

سوال خلاقیت سال 87(سوال 8)

در نسخه ای خطی از يک رساله ی قديمی رياضی آمده است:

این رساله در زمانی به پایان رسید که اگر 13 مرتبه در خودش ضرب کنیم عدد عظیم زیر حاصل میشود

رساله در چه سالی به پايان رسيده است؟ ثابت کنيد!

به نظر من ساده ترین سوال خلاقیت توی این 3 سال اخیر بوده !!!(البته وسطش کلی متنم داشت که مهم نیست )

 

[Aref]

پاسخ : مسابقه ریاضی ((حل کنید !))

خب یه تقریب بزنید که عددش بین چه اعدادیه. بعد از هم نهشتی استفاده کنید.

 

[ash1374]

پاسخ : مسابقه ریاضی ((حل کنید !))

سوال بعدی. باز هم هندسه:

مثلث abc و m وسط bc مفروضند. فرض کنید am دایره ی محاطی داخلی مثلث را در pوq قطع کند. از pوq خطوطی موازی bc رسم می کنیم تا دایره محاطی را برای بار دوم در tوs قطع کنند. Asوat ضلع bc را در d و e قطع کرده اند. ثابت کنید m وسط de نیز هست.

پ.ن : ببخشید پست بالایی رو ندیدم . رو این بعدا فکر کنید.

 

[Aref]

پاسخ : مسابقه ریاضی ((حل کنید !))

سوال بعدی. باز هم هندسه:

مثلث abc و m وسط bc مفروضند. فرض کنید am دایره ی محاطی داخلی مثلث را در pوq قطع کند. از pوq خطوطی موازی bc رسم می کنیم تا دایره محاطی را برای بار دوم در tوs قطع کنند. Asوat ضلع bc را در d و e قطع کرده اند. ثابت کنید m وسط de نیز هست.

پ.ن : ببخشید پست بالایی رو ندیدم . رو این بعدا فکر کنید.

راهنمایی:
همساز بزنید.

 

[math]

پاسخ : مسابقه ریاضی ((حل کنید !))

راه حل خودم :

حال از اون جایی که یکانش 3 است پس عدد مورد نظر برابر 183 است!!!!

 

[hkh74]

پاسخ : مسابقه ریاضی ((حل کنید !))

اول از تالس برای محاسبه ی طول دو پاره خطی که سوال برابریشون رو از ما می خواد استفاده می کنیم، بعد نتیجه می گیریم کافیه ثابت کنیم

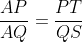. این هم با توجه به اینکه قطبی A نسبت به دایره ی محاطی ، عمود وارد از I بر BC و میانه ی AM همرسند با استفاده از همساز (که Aref گفتن) ثابت میشه.