دوستان اگر راه حل و یا نظری در باره ی هریک از سوالات آزمون دارند، می توانند در این تاپیک مطرح کنند:
سوال 1. (صورت اصلاح شده)
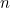 مین در یک زمین کاشته شده است که سه تا از این مین ها فعال اند و ممکن است منفجر شوند و بقیه غیر فعال اند. یک دستگاه مین یاب داریم که در هر بار استفاده، می توان ار میان تعداد دلخواهی مین، مشخص کرد که تعداد مین های فعال برابر 0، 1 و یا بیش از یکی است. فرض کنید
مین در یک زمین کاشته شده است که سه تا از این مین ها فعال اند و ممکن است منفجر شوند و بقیه غیر فعال اند. یک دستگاه مین یاب داریم که در هر بار استفاده، می توان ار میان تعداد دلخواهی مین، مشخص کرد که تعداد مین های فعال برابر 0، 1 و یا بیش از یکی است. فرض کنید
 کمترین تعداد استفاده از مین یاب برای پیدا کردن مین های فعال است.
کمترین تعداد استفاده از مین یاب برای پیدا کردن مین های فعال است.
الف)
 را به دست آورید.
را به دست آورید.
ب) ثابت کنید
 .
.
سوال 2.
دنباله ی
 به صورت زیر تعریف شده است:
به صورت زیر تعریف شده است:
[center:e5e45ab54e]

[/center:e5e45ab54e]ثابت کنید همه ی جملات دنباله، اعدادی صحیح اند.
سوال 3.
فرض کنید
 مرکز دایره ی محیطی مثلث حاده الزاویه ی
مرکز دایره ی محیطی مثلث حاده الزاویه ی
 است. محل برخورد
است. محل برخورد
 و
و
 را
را
 و محل برخورد
و محل برخورد
 و
و
 را
را
 می نامیم. ثابت کنید
می نامیم. ثابت کنید
 اگر و فقط اگر
اگر و فقط اگر
 .
.
سوال 1. (صورت اصلاح شده)
الف)
ب) ثابت کنید
سوال 2.
دنباله ی
[center:e5e45ab54e]
[/center:e5e45ab54e]ثابت کنید همه ی جملات دنباله، اعدادی صحیح اند.
سوال 3.
فرض کنید


































