ترکیبیات مرحله دویی
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ترکیبیات مرحله دویی
این هست اما من یه راه حل دیگه دارم که تو mathlinks مذمونی ازش ندیدم:
جایگاه اعداد 1 تا 2001 را در نظر میگیریم چون 2002 ستون و سطر داریم پس حداقل یک سطر و یک ستون داریم که از اعدادی بجز اعداد 1 تا 2001 تشکیل شده است.
یعنی از اعداد 2002 تا 2002*2002 تشکیل شده است.
چون حداقل مقدار ab برابر 2002*2003 است و حداکثر مقدار c برابر 2002*2002 است پس این کار امکان پذیر نیست چون در آن به ازای خانه تقاطع آن سطر و ستون اعداد a,b,c وجود ندارند که ab=c
این هست اما من یه راه حل دیگه دارم که تو mathlinks مذمونی ازش ندیدم:
جایگاه اعداد 1 تا 2001 را در نظر میگیریم چون 2002 ستون و سطر داریم پس حداقل یک سطر و یک ستون داریم که از اعدادی بجز اعداد 1 تا 2001 تشکیل شده است.
یعنی از اعداد 2002 تا 2002*2002 تشکیل شده است.
چون حداقل مقدار ab برابر 2002*2003 است و حداکثر مقدار c برابر 2002*2002 است پس این کار امکان پذیر نیست چون در آن به ازای خانه تقاطع آن سطر و ستون اعداد a,b,c وجود ندارند که ab=c
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ترکیبیات مرحله دویی
خط ها رو به ترتیب
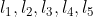می نامیم .
میایم نقطه ها رو برمیداریم و خودمون میچینیم . بدترین حالت حالتی هستش که نقاط رو نقطه همرسی دو خط باشند و بدتر از اون حالت حالتی هستش که همه خطوط همرس باشند و یکی از نقاط ما همون نقطه همرسی باشه
پس 4 تا نقطه داریم الان و پنج خط همرس.در واقع اگه همه همرس نباشند ما باید بیش از یه نقطه مصرف کنیم برای پر کردن نقطه همرسی ها.
. دو خطی رو که از همه کمتر نقطه هست روشون رو انتخاب میکنیم که مجموع نقاط روی اونها حداکثر سه هستش ( یکی نقطه همرسی هستش و اگر هم روی هر خط یه نقطه باشه اونوقت حالت حداکثر هر خط هستش که میشه سه تا ) . حالا این دو تا خط رو انتخاب میکنیم و چون حداکثر سه تا نقطه روشون بود پس حداقل دو تا نقطه داریم که روی این دوتا نیست پس اون دو تا نقطه رو انتخاب میکنیم.
البته میدونم راه حلم یه جوریه !!!
خط ها رو به ترتیب
میایم نقطه ها رو برمیداریم و خودمون میچینیم . بدترین حالت حالتی هستش که نقاط رو نقطه همرسی دو خط باشند و بدتر از اون حالت حالتی هستش که همه خطوط همرس باشند و یکی از نقاط ما همون نقطه همرسی باشه
پس 4 تا نقطه داریم الان و پنج خط همرس.در واقع اگه همه همرس نباشند ما باید بیش از یه نقطه مصرف کنیم برای پر کردن نقطه همرسی ها.
. دو خطی رو که از همه کمتر نقطه هست روشون رو انتخاب میکنیم که مجموع نقاط روی اونها حداکثر سه هستش ( یکی نقطه همرسی هستش و اگر هم روی هر خط یه نقطه باشه اونوقت حالت حداکثر هر خط هستش که میشه سه تا ) . حالا این دو تا خط رو انتخاب میکنیم و چون حداکثر سه تا نقطه روشون بود پس حداقل دو تا نقطه داریم که روی این دوتا نیست پس اون دو تا نقطه رو انتخاب میکنیم.
البته میدونم راه حلم یه جوریه !!!
آخرین ویرایش توسط مدیر
پاسخ : ترکیبیات مرحله دویی
اصلا بدیهی نیست که این بدترین حالته. این که برای پر کردن همرسی ها کمترین نقاط تو این حالت بدست میاد دلیل نمیشه. شاید مثلا تو حالتی که سه تا توی یه نقطه همرس باشن و دو تا توی یه نقطه دیگه اتفاقات دیگه ای بیفته و ... . خلاصه سعی کنید هیچ وقت این جور راه حل ها رو بکار نبرید. معمولا تو مرحله دو نمره ای نمیگیرین. هر ادعایی باید دقیق ثابت بشه مگر اینکه جز دانسته های قبلیمون باشه. پس بیشتر دقت کنید:3:
خط ها رو به ترتیب
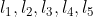می نامیم .
میایم نقطه ها رو برمیداریم و خودمون میچینیم . بدترین حالت حالتی هستش که نقاط رو نقطه همرسی دو خط باشند و بدتر از اون حالت حالتی هستش که همه خطوط همرس باشند و یکی از نقاط ما همون نقطه همرسی باشه
پس 4 تا نقطه داریم الان و پنج خط همرس.در واقع اگه همه همرس نباشند ما باید بیش از یه نقطه مصرف کنیم برای پر کردن نقطه همرسی ها.
. دو خطی رو که از همه کمتر نقطه هست روشون رو انتخاب میکنیم که مجموع نقاط روی اونها حداکثر سه هستش ( یکی نقطه همرسی هستش و اگر هم روی هر خط یه نقطه باشه اونوقت حالت حداکثر هر خط هستش که میشه سه تا ) . حالا این دو تا خط رو انتخاب میکنیم و چون حداکثر سه تا نقطه روشون بود پس حداقل دو تا نقطه داریم که روی این دوتا نیست پس اون دو تا نقطه رو انتخاب میکنیم.
البته میدونم راه حلم یه جوریه !!!
میایم نقطه ها رو برمیداریم و خودمون میچینیم . بدترین حالت حالتی هستش که نقاط رو نقطه همرسی دو خط باشند و بدتر از اون حالت حالتی هستش که همه خطوط همرس باشند و یکی از نقاط ما همون نقطه همرسی باشه
پس 4 تا نقطه داریم الان و پنج خط همرس.در واقع اگه همه همرس نباشند ما باید بیش از یه نقطه مصرف کنیم برای پر کردن نقطه همرسی ها.
. دو خطی رو که از همه کمتر نقطه هست روشون رو انتخاب میکنیم که مجموع نقاط روی اونها حداکثر سه هستش ( یکی نقطه همرسی هستش و اگر هم روی هر خط یه نقطه باشه اونوقت حالت حداکثر هر خط هستش که میشه سه تا ) . حالا این دو تا خط رو انتخاب میکنیم و چون حداکثر سه تا نقطه روشون بود پس حداقل دو تا نقطه داریم که روی این دوتا نیست پس اون دو تا نقطه رو انتخاب میکنیم.
البته میدونم راه حلم یه جوریه !!!
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ترکیبیات مرحله دویی
خب بله حرف شما کاملا متین هستش . خودمم هم همین طوری فکر میکردم . بخاطر همین گفتم که یه جوریه !!
خب حالا میایم اون دو تا خطی رو انتخاب می کنیم که از همه کمتر نقطه رو شون هست.
اگه نشون بدیم مجموع نقاط روی این دوتا حداکثر 3 تاست مساله حل میشه چون حداقل دو نقطه هست که روی این دوتا خط نیست.
پس فرض خلف می زنیم میگیم حداقل 4 تا نقطه رو این دو خط وجود داشته باشه.اگه یکی از این چهار تا نقطه همرسی باشه پس هر کدوم یکی نقطه دارند و یه نقطه هم همرسی هست ( همرسی رو دو بار شمردیم.)اینطوری دقیقا دو نقطه وجود داره که بیرون از این خطوط هستش پس مساله حل شد
اما اگه نقطه همرسی این دو خط نقطه ما نباشه پس یا هرکدوم به تنهایی دو تا دارند یا یکی سه تا داره اون یکی یکی یا یکی چهار تا داره اون یکی هیچی
حالت آخر به راحتی تناقض داره چون اول گفتیم خطوطی رو انتخاب کردیم که از همه کمتر نقطه دارند پس بقیه سه تاخط دیگه حداقل چهار تا نقطه رو دارند پس باید روی اون خطی که چهارتا نقطه داره منطبق شوند که تناقضه
حالت دیگه اینه که یکی سه تا باشه اون یکی یکی،پس بقیه سه تا خط دیگه حداقل سه تا نقطه دارند.این هم تناقض داره . اگه شکلشو بکشید خیلی بدیهیه.
حالا اگه دوتا دوتا باشه . پس بقیه حداقل دو تا دارند.
حالا اون نقطه ای که بیرون هستش رو در نظر میگیریم و اسمشو میذاریم p
حالا الان سه تا خط دیگه باید باشه که حداقل از دو تا نقطه بگذره پس ما الان 8 تا خط میتونیم داشته باشیم که سه تاش مراد هست (اینم اگه شکل بکشید متوجه منظورم میشید)
این رو هم با حالت بندی رو تعداد خطوطی که از p میگذره بشه حل کرد مثلا یکی ، دوتا یا سه تا.
خب بله حرف شما کاملا متین هستش . خودمم هم همین طوری فکر میکردم . بخاطر همین گفتم که یه جوریه !!
خب حالا میایم اون دو تا خطی رو انتخاب می کنیم که از همه کمتر نقطه رو شون هست.
اگه نشون بدیم مجموع نقاط روی این دوتا حداکثر 3 تاست مساله حل میشه چون حداقل دو نقطه هست که روی این دوتا خط نیست.
پس فرض خلف می زنیم میگیم حداقل 4 تا نقطه رو این دو خط وجود داشته باشه.اگه یکی از این چهار تا نقطه همرسی باشه پس هر کدوم یکی نقطه دارند و یه نقطه هم همرسی هست ( همرسی رو دو بار شمردیم.)اینطوری دقیقا دو نقطه وجود داره که بیرون از این خطوط هستش پس مساله حل شد
اما اگه نقطه همرسی این دو خط نقطه ما نباشه پس یا هرکدوم به تنهایی دو تا دارند یا یکی سه تا داره اون یکی یکی یا یکی چهار تا داره اون یکی هیچی
حالت آخر به راحتی تناقض داره چون اول گفتیم خطوطی رو انتخاب کردیم که از همه کمتر نقطه دارند پس بقیه سه تاخط دیگه حداقل چهار تا نقطه رو دارند پس باید روی اون خطی که چهارتا نقطه داره منطبق شوند که تناقضه
حالت دیگه اینه که یکی سه تا باشه اون یکی یکی،پس بقیه سه تا خط دیگه حداقل سه تا نقطه دارند.این هم تناقض داره . اگه شکلشو بکشید خیلی بدیهیه.
حالا اگه دوتا دوتا باشه . پس بقیه حداقل دو تا دارند.
حالا اون نقطه ای که بیرون هستش رو در نظر میگیریم و اسمشو میذاریم p
حالا الان سه تا خط دیگه باید باشه که حداقل از دو تا نقطه بگذره پس ما الان 8 تا خط میتونیم داشته باشیم که سه تاش مراد هست (اینم اگه شکل بکشید متوجه منظورم میشید)
این رو هم با حالت بندی رو تعداد خطوطی که از p میگذره بشه حل کرد مثلا یکی ، دوتا یا سه تا.
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : ترکیبیات مرحله دویی
هر ستون و ردیف را شماره گذاری میکنیم و در خانه ای که در ستون i و سطر j هست عدد i+j را مینویسیم بدین ترتیب مجموع اعداد خانه ی این رخ ها میشه 72.
حالا میدونیم اعداد خانه سیاه فرد هستند و سفید ها زوج هستند پس اگه تعداد رخ های سفید فرد باشه مجموع اعداد رخ ها فرد میشه که تناقضه پس باید زوج باشه
هر ستون و ردیف را شماره گذاری میکنیم و در خانه ای که در ستون i و سطر j هست عدد i+j را مینویسیم بدین ترتیب مجموع اعداد خانه ی این رخ ها میشه 72.
حالا میدونیم اعداد خانه سیاه فرد هستند و سفید ها زوج هستند پس اگه تعداد رخ های سفید فرد باشه مجموع اعداد رخ ها فرد میشه که تناقضه پس باید زوج باشه
پاسخ : ترکیبیات مرحله دویی
حسن و حسین میخواند 25 سکه به ارزش 1,2,...,25 را بین خود تقسیم کنند.در هر مرحله یکی از آنها یک سکه انتخاب میکند و نفر دیگر تصمیم میگیرد که سکه را چه کسی بردارد.اولین انتخاب را حسن انجام میدهد و پس از آن در هر مرحله کسی سکه انتخاب میکند که در آن لحظه پول بیشتری داشته باشد.اگر در مرحله ای هر دو نفر به یک اندازه پول داشته باشند،کسی که در مرحله قبل سکه انتخاب کره بود،سکه انتخاب میکند.در پایان کسی که پول بیشتری داشته باشد،سکه انتخاب میکند.چه کسی استراتژی برد دارد؟
راهنمایی:به ذسته های روبه رو تقسیم کنید
)1و25()2و24(و...)12و14)و دسته 13
حسن و حسین میخواند 25 سکه به ارزش 1,2,...,25 را بین خود تقسیم کنند.در هر مرحله یکی از آنها یک سکه انتخاب میکند و نفر دیگر تصمیم میگیرد که سکه را چه کسی بردارد.اولین انتخاب را حسن انجام میدهد و پس از آن در هر مرحله کسی سکه انتخاب میکند که در آن لحظه پول بیشتری داشته باشد.اگر در مرحله ای هر دو نفر به یک اندازه پول داشته باشند،کسی که در مرحله قبل سکه انتخاب کره بود،سکه انتخاب میکند.در پایان کسی که پول بیشتری داشته باشد،سکه انتخاب میکند.چه کسی استراتژی برد دارد؟
راهنمایی:به ذسته های روبه رو تقسیم کنید
)1و25()2و24(و...)12و14)و دسته 13
- ارسال ها
- 2
- لایک ها
- 0
- امتیاز
- 0
حسن و حسین
نفر دوم (حسن) استراتژی برد دارد:
فرض کنید در اولین حرکت نفر اول (حسین) سکه ی x را انتخاب می کند.
اگر نفر دوم (حسن) این سکه را برای خود برداشت و در ادامه ی بازی نتوانست راهی برای بردن پیدا کند،
این سکه را به نفر اول (حسین) می دهد. در این صورت از مرحله ی بعد جای حسن و حسین عوض می شود و نفر اول (حسین) نمی تواند ببرد.
------- سوال جدید --------
گرافی همبند و 1000 راسی داریم ثابت کنید می توان 90 راس از این گراف را می توان رنگ کرد ، به طوری که فاصله ی هر راس دیگر تا یکی از رئوس رنگی حداکثر برابر 10 باشد.
مثالی ارائه دهید که نشان بدهد 90 بهترین کران است.
نفر دوم (حسن) استراتژی برد دارد:
فرض کنید در اولین حرکت نفر اول (حسین) سکه ی x را انتخاب می کند.
اگر نفر دوم (حسن) این سکه را برای خود برداشت و در ادامه ی بازی نتوانست راهی برای بردن پیدا کند،
این سکه را به نفر اول (حسین) می دهد. در این صورت از مرحله ی بعد جای حسن و حسین عوض می شود و نفر اول (حسین) نمی تواند ببرد.
------- سوال جدید --------
گرافی همبند و 1000 راسی داریم ثابت کنید می توان 90 راس از این گراف را می توان رنگ کرد ، به طوری که فاصله ی هر راس دیگر تا یکی از رئوس رنگی حداکثر برابر 10 باشد.
مثالی ارائه دهید که نشان بدهد 90 بهترین کران است.
آخرین ویرایش توسط مدیر