ذوزنقه متساوی الساقین

ash1374 · 1391/12/5

سلام دوستان. چند وقت پیش این سوال رو اتفاقی طرح کردم ولی بجز همون راهی که سوال باش طرح شده راه خوب دیگه ای براش پیدا نکردم:178:. ممنون میشم اگه راه حلی دارید بگید.

در ذوزنقه ی متساوی الساقین ABCD که CD قائده ی بزرگ است جمع طول قائده ی بزرگ و قطر، 3 برابر طول یک ساق است. اگر

$I_{1}$

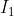و

$I_{2}$

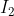به ترتیب مرکز دوایر محاطی داخلی مثلث های ACD و ABC باشند ثابت کنید مثلث

$AI_{1}I_{2}$

متساوی الساقین است.

mntjmath · 1391/12/5

پاسخ : ذوزنقه متساوی الساقین

پاي عمود وارد از

$I_{1}$

بر

$AC$

را

$E$

بگيريد.با توجه به اينكه

$\frac{AC+CD-AD}{2}=EC$

و استفاده از شرط مسئله

$EC=AD=BC$

.پس با توجه به نيمساز بودن

$CI_{}2$

مثلث هاي

$CI_{2}E$

و

$CI_{2}B$

برابرند. پس

$\widehat{I_{2}EC}=\widehat{I_{2}BC}=\frac{\widehat{B}}{2}$

در نتيجه

$\widehat{I_{1}EI_{2}}=90+\frac{\widehat{B}}{2}$

و از ان جا كه

$\widehat{I_{2}CI_{1}}=\frac{\widehat{C}}{2}$

و

$90=\frac{\widehat{C}}{2}+\frac{\widehat{B}}{2}$

پس

$I_{1}EI_{2}C$

محاطي است.در نتيجه

$\widehat{ECI_{1}}=\widehat{EI_{2}I_{1}}$

همچنين داريم

$\widehat{I_{2}AE}=\widehat{ECI_{1}}$

پس

$\widehat{EI_{2}I_{1}}=\widehat{I_{2}AE}$

پس

$\widehat{AI_{2}I_{1}}=\widehat{AI_{2}E}+\widehat{EI_{2}I_{1}}=\widehat{AI_{2}E}+\widehat{EAI_{2}}=\widehat{I_{2}EC}=\frac{\widehat{B}}{2}$

همچنين به وضوح

$\widehat{I_{2}AI_{1}}=\frac{\widehat{B}}{2}$

در نتيجه

$AI_{1}=I_{1}I_{2}$

.

اقا اگه از اين سوالا بازم طرح كردي بزار لذت ببريم :3:

ash1374 · 1391/12/5

پاسخ : ذوزنقه متساوی الساقین

mntjmath گفت

ممنون استاد. عالی بود.

گفتم که،تابستون قبلی کاملا اتفاقی از یه لم بدست اومد.

راه خودم:

$CI_{2}$

رو امتداد می دیم تا دایره ی محیطی ذوزنقه رو تو M قطع کنه.M وسط کمان AB هستش. پس MA=MI2. واضحه که

$\measuredangle MAI_{1}=90$

. اگه بگیم

$\measuredangle MI_{2}I_{1}=90$

اونوقت MAI1I2 کایت میشه و حله. یعنی کافیه بگیم

$MAI_{1}I_{2}$

محاطیه. کافیه بگیم

$\measuredangle I_{1}MI_{2}=\measuredangle I_{1}AI_{2}=\frac{\measuredangle A}{2}$

. یعنی کافیه

$\measuredangle I_{1}MI_{2}$

رو حساب کنیم. اگه MI1 رو ادامه بدیم تا دایره رو تو T قطع کنه طبق قضیه ای داریم T نقطه ی mixtilinear مثلث acd هستش. حالا واضحه

$\measuredangle I_{1}MI_{2}=\measuredangle CMT=\measuredangle CAT$

. پس کافیه CAT رو حساب کنیم. میدانیم خطی که از یه راس به نقطه mixtilinear میاد قرینه ی خطی است که از اون راس به مماس دایره محاطی خارجی میاد نسبت به نیمساز . پس اگه مماس دایره محاطی خارجی مثلث ACD به CD مثلا E باشه

$\measuredangle I_{1}MI_{2}=\measuredangle CAT=\measuredangle DAE$

. از فرض بدست میاد AD=DE و نتیجه میشه

$\measuredangle I_{1}MI_{2}=\measuredangle CAT=\measuredangle DAE=90-\frac{D}{2}=\frac{\measuredangle A}{2}$

. که حکم رو نتیجه میده.

mntjmath · 1391/12/5

پاسخ : ذوزنقه متساوی الساقین

هم خطي وسط كمان و مركز نيم سازي و mixtilinear يكي از همخطي هاي مورد علاقه منه و واقعا زيباست و اين راه حل هم به نظر من عاليه.

يكم كه داشتم شكلو بررسي مي كردم به چيزاي جالبي برخوردم.همين شكل پر خواص قشنگه.يه سري حدسم دارم كه بايد روشون كار كنم اگه به نتيجه ي خوبي رسيدم مطرح مي كنمشون

-ممنون از اين سوال زيبا-

MBGO · 1391/12/6

پاسخ : ذوزنقه متساوی الساقین

ash1374 گفت

*** من I_1 رو مرکز دایره محاطیه ABC گرفتم

e , f محل تماس (i_2) با ac , dc از شرط مساله داریم cf=ce=cd :

Bi_1ea محاطی , b,i_1,f همخط،، ci_1i_2f محاطی ، پس ci_1 عمود بر i_1i_2 , be عمود است، پس be,i_1i_2 موازی اند، نتیجتا ai_1i_2 برابر با مجموع نصف bac ,abe است،که برابر با bec شده،چون ce,cb برابر ند پس bec=نصف bad بوده و حکم اثبات شد.

ذوزنقه متساوی الساقین

ash1374

New Member

mntjmath

New Member

ash1374

New Member

mntjmath

New Member

MBGO

New Member