سوالات ترکیبیات مقدماتی(سری 1)

rezashiri · 1389/4/24

سلام. چند تا سوال ترکیبیاتی از اصول شمارش:

سوال اول:چند عدد از مجموعه {A={1,2,3,...,100000 دقیقا یک رقم 5 دارند؟

سوال دوم:در چند زیر مجموعه از مجموعه {A={1,2,3,...,10 اختلاف کوچکترین و بزرگترین عضو برابر 5 می باشد و تعداد اعضا عددی زوج است؟

سوال سوم:کلیه اعداد زوج چهار رقمی با ارقام متمایز را روی کاغذ نوشته ایم ، مجموع این اعداد را بیابید.

سوال چهارم:عددی را مقلوب کامل می گوییم که با مقلوب خود برابر باشد ، چند عدد مقلوب کامل کمتر از 1000000 وجود دارد؟

سوال پنچم:به ازای چند عدد چهار رقمی مانند

$\overline{abcd}$

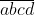مجموع دو عدد

$\overline{ab}$

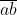و

$\overline{cd}$

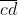عددی فرد است؟

counterexample · 1389/4/24

1) 4^9 * 5
=32805
درسته؟

4) 2*999
دلیل:
تعداد حالات برای اعداد فرد رقمی): 999 حالت برای سه رقم سمت چپ (بقیه به صورت یکتا تعیین میشوند)
تعداد حالات برای اعداد زوج رقمی): 999 حالت برای سه رقم سمت چپ (بقیه به صورت یکتا تعیین میشوند)
البته اگه منظور اعداد صحیح نامنفی باشد: 999*2+1=1999
درسته؟

rezashiri · 1389/4/24

vasebad گفت

بله، درسته.

لطفا از این به بعد یکمی توضیح بدید.

rezashiri · 1389/4/24

نه ، درست نیست.

چطوری برای 3 رقم سمت چپ 999 حالت داریم؟

بعدشم مثلا برای اعداد یک رقمی چی؟

Olympiad · 1389/4/24

سوال 2 :

$2^3\times5$

از اين نكته بايد استفاده كرد كه مجموعه هاي فرد عضوي و زوج عضوي هر مجموعه برابر

$2^{n-1}$

مي باشد
==============================================================================
سوال 3 :
سوال 3 رو هم كه برنامشو مي نويسي وحل ميشه!!!!!!!!
اگه بخوايد اين سوال رو حل كنيد بايد ببنيد هر عدد چند بار و در چه مكان هايي ظاهر شده و مجموع يكان ها و دهگان ها و.................
===============================================================================
سوال 4‌:

$9+9\times10\times2+9\times10^2\times2$

1 : 9 حالت براي اعداد 2 رقمي
2 : اگر 2 رقم اول عدد 3 رقمي را مشخص كنيم رقم سوم نيز مشخص مي شود پس مي شود :

$9\times10$

3 : اگر 2 رقم اول عدد 4 رقمي را مشخص كنيم رقم سوم و چهارم نيز مشخص مي شود پس مي شود :

$9\times10$

4 : اگر 3 رقم اول عدد 5 رقمي را مشخص كنيم رقم چهارم و پنجم نيز مشخص مي شود پس مي شود :

$9\times10^2$

5 : اگر 3 رقم اول عدد 6 رقمي را مشخص كنيم رقم چهارم و پنجم و ششم نيز مشخص مي شود پس مي شود :

$9\times10^2$

=========================================================================
سوال 5 :

$9\times10\times10\times5$

اگر b به 10 طريق انتخاب شود آنگاه 5 حالت براي d مي ماند (5 عدد زوج يا 5 عدد فرد)

rezashiri · 1389/4/24

Olympiad گفت

سوال 2 :

$2^3\times5$

از اين نكته بايد استفاده كرد كه مجموعه هاي فرد عضوي و زوج عضوي هر مجموعه برابر

$2^{n-1}$

مي باشد
==============================================================================
سوال 3 :
سوال 3 رو هم كه برنامشو مي نويسي وحل ميشه!!!!!!!!
اگه بخوايد اين سوال رو حل كنيد بايد ببنيد هر عدد چند بار و در چه مكان هايي ظاهر شده و مجموع يكان ها و دهگان ها و.................
===============================================================================
سوال 4‌:

$9+9\times10\times2+9\times10^2\times2$

1 : 9 حالت براي اعداد 2 رقمي
2 : اگر 2 رقم اول عدد 3 رقمي را مشخص كنيم رقم سوم نيز مشخص مي شود پس مي شود :

$9\times10$

3 : اگر 2 رقم اول عدد 4 رقمي را مشخص كنيم رقم سوم و چهارم نيز مشخص مي شود پس مي شود :

$9\times10$

4 : اگر 3 رقم اول عدد 5 رقمي را مشخص كنيم رقم چهارم و پنجم نيز مشخص مي شود پس مي شود :

$9\times10^2$

5 : اگر 3 رقم اول عدد 6 رقمي را مشخص كنيم رقم چهارم و پنجم و ششم نيز مشخص مي شود پس مي شود :

$9\times10^2$

=========================================================================
سوال 5 :

$9\times10\times10\times5$

اگر b به 10 طريق انتخاب شود آنگاه 5 حالت براي d مي ماند (5 عدد زوج يا 5 عدد فرد)

کاملا درسته.

حالا برای سوال 4 یک راه حل کلی پیدا کنید.

Olympiad · 1389/4/24

راه حل كلي براي سوال 4 منظوررتون تا عدد

$10^n$

هست؟!

rezashiri · 1389/4/24

Olympiad گفت

برای اعداد n رقمی.

Olympiad · 1389/4/24

حالت كلي براي اعداد رقمي

$n$

برابر است با :

$9\times10^{(\left \lceil \frac{n}{2}\right \rceil-1)}$

rezashiri · 1389/4/24

Olympiad گفت

این که نمیشه.
مثلا برای اعداد 1 رقمی طبق این فرمول چی می شه!؟؟!!!!

راهنمایی: ارقام رو زوج و فرد کنید.

Olympiad · 1389/4/24

rezashiri گفت

بابا چرا اينقدر كارو سخت مي كنيد براي هر

$n> 1$

اين فرمول برقراره و براي

$n= 1$

هيچ چي!!!!!!!!

counterexample · 1389/4/25

rezashiri گفت

تعداد حالات برای اعداد فرد رقمی): 5 جایگاه در نظر میگیریم و 999 حالت برای سه رقم سمت چپ (بقیه به صورت یکتا تعیین میشوند)
تعداد حالات برای اعداد زوج رقمی): 6 جایگاه در نظر میگیریم و 999 حالت برای سه رقم سمت چپ (بقیه به صورت یکتا تعیین میشوند)

rezashiri · 1389/4/25

vasebad گفت

rezashiri گفت

تعداد حالات برای اعداد فرد رقمی): 5 جایگاه در نظر میگیریم و 999 حالت برای سه رقم سمت چپ (بقیه به صورت یکتا تعیین میشوند)
تعداد حالات برای اعداد زوج رقمی): 6 جایگاه در نظر میگیریم و 999 حالت برای سه رقم سمت چپ (بقیه به صورت یکتا تعیین میشوند)

به نظر من راحت اشتباهه.

اگه خودت فکر می کنی درسته می شه با مثال توضیح بدی تا منم بفهمم.؟!

counterexample · 1389/4/25

rezashiri گفت

میدانیم که تمامی جواب ها 1 تا 5 رقمی اند.
پس 5 جایگاه در نظر میگیریم.

حال

$\binom{5}{1}$

حالت برای انتخاب جایگاهی برای عدد پنج وجود دارد.

بقیه جایگاه ها نیز 9 حالت دارند (اعداد 0 تا 9 بغیر از 5)

پس نتیجه میگیریم جواب برابر است با:

$\binom{5}{1}\times 9^{4}$

سوالات ترکیبیات مقدماتی(سری 1)

rezashiri

Well-Known Member

counterexample

Guest

rezashiri

Well-Known Member

rezashiri

Well-Known Member

Olympiad

New Member

rezashiri

Well-Known Member

Olympiad

New Member

rezashiri

Well-Known Member

Olympiad

New Member

rezashiri

Well-Known Member

Olympiad

New Member

counterexample

Guest

rezashiri

Well-Known Member

counterexample

Guest