سوالی از بلغارستان (ترکیبیات)
- شروع کننده موضوع Goharshady
- تاریخ شروع
- برچسپ ها اعداد المپیاد المپیاد جهانی المپیاد ریاضی ترکیبیات دنباله ریاضی عدد طبیعی کتاب
- ارسال ها
- 2,239
- لایک ها
- 166
- امتیاز
- 0
درست یا نادرستشو دقیقا نمی دونم.(روابط بازگشتی باید با توضیح همراه باشند تا فهمیده شوند!!)
شما راه حلتو بنویس. مهم جواب نیست ، مهم راه حله!!
من خودم مستقیم جوابو به دست آورده بودم که دو تا سیگما داخل هم بود ، وقتی پاسخ المپیاد رو نگاه کردم هم همینطوری مستقیم بود.
حالا شما راهتو بنویس! احتمالا خیلی بهتر باشه .
فقط یک مشکل کوچولو هم هست :
در المپیاد جهانی باید شکل بسته (صریح) دنباله را بنویسید و بازگشتی قبول نمی کنند.
ولی شما بازگشتی رو ثابت کن ، من رابطه بازگشتی رو حل می کنم!
شما راه حلتو بنویس. مهم جواب نیست ، مهم راه حله!!
من خودم مستقیم جوابو به دست آورده بودم که دو تا سیگما داخل هم بود ، وقتی پاسخ المپیاد رو نگاه کردم هم همینطوری مستقیم بود.
حالا شما راهتو بنویس! احتمالا خیلی بهتر باشه .
فقط یک مشکل کوچولو هم هست :
در المپیاد جهانی باید شکل بسته (صریح) دنباله را بنویسید و بازگشتی قبول نمی کنند.
ولی شما بازگشتی رو ثابت کن ، من رابطه بازگشتی رو حل می کنم!
مسئله را اينطوري تقسيم ميكنيم كه :
بزرگترين عدد در مكان چندم قرار ميگيرد :
1 ) اگر آخرين عدد باشد بقيه ي اعداد به
با شرط مسئله ميتوانند قرار گيرند .
اگر توجه كنيم اگر بزرگترين عدد در مكان اول و آخر نباشد همه ي اعداد پشت سر آن و جلوي آن به صورت صعودي قرار ميگيرند . بنابر اين در هر مرحله كه بزرگترين عدد را در يك مكان در نظر ميگيريم اعداد پشت آن را انتخاب و بقيه ي اعداد را جلوي آن در نظر ميگيريم و چون بايد به ترتيب صعودي باشند فقط به يك طريق ميشود يعني :
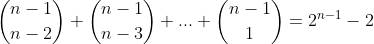
پس جواب ميشه
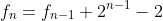
خيلي بد توضيح دادم خودمم هيچ چي نفهميدم !!
بزرگترين عدد در مكان چندم قرار ميگيرد :
1 ) اگر آخرين عدد باشد بقيه ي اعداد به
اگر توجه كنيم اگر بزرگترين عدد در مكان اول و آخر نباشد همه ي اعداد پشت سر آن و جلوي آن به صورت صعودي قرار ميگيرند . بنابر اين در هر مرحله كه بزرگترين عدد را در يك مكان در نظر ميگيريم اعداد پشت آن را انتخاب و بقيه ي اعداد را جلوي آن در نظر ميگيريم و چون بايد به ترتيب صعودي باشند فقط به يك طريق ميشود يعني :
پس جواب ميشه
خيلي بد توضيح دادم خودمم هيچ چي نفهميدم !!
- ارسال ها
- 2,239
- لایک ها
- 166
- امتیاز
- 0
من هر کار کردم نتونستم این رابطه ی بازگشتی رو حل کنم! خیلی حل کردنش سخته!! لااقل چیزی بیشتر از ترکیبیات لازم داره. (بچه هایی که جبرشون قویه حل کنن!!)
اما راه حل من که شبیه راه حل کتاب هم بود (کتاب رقابتهای المپیاد ریاضی ، تیتو آندرسکو) اینجوریه:
به ازای یک i دلخواه فرض می کنیم
باشد. اعداد را از چپ به راست نوشته ایم(!) می دانیم دنباله های سمت راست (بعد از a[SUB]i+1[/SUB] با احتساب خودش) و سمت چپ (یعنی a[SUB]i[/SUB] و قبل از آن) اکیدا صعودی هستند. می دانیم a[SUB]i+1[/SUB] از همه ی اعداد بعد از خود و a[SUB]i[/SUB] کوچکتر است. اگر a[SUB]i+1[/SUB]=k داریم :
[center:1df9153247]
-1\rightarrow&space;k<i\rightarrow&space;k\leq&space;i-1)
[/center:1df9153247]
[/center:1df9153247]
من این راه رو رفتم چون می دونستم که بازگشتی قبول نمی کنن. ولی راه شما هم کاملا درسته. تو کتاب با یه سری محاسبات دیگه به همین رسیده بود و بعد ساده کرده بود. (البته توضیح داده بود که ساده کردنش مهم نیست به همین دلیل من هم ساده نمی کنم!!)
اما راه حل من که شبیه راه حل کتاب هم بود (کتاب رقابتهای المپیاد ریاضی ، تیتو آندرسکو) اینجوریه:
به ازای یک i دلخواه فرض می کنیم
[center:1df9153247]
باید یک عدد بزرگتر از k برای هر یک از جاهای بعدش انتخاب کنیم. یعنی باید n-i-1 عدد بزرگتر از k انتخاب کنیم و همه ی آنها را به صورت صعودی پس از k قرار دهیم. سپس بقیه اعداد را به صورت صعودی قبل از k قرار دهیم. پس جواب برابر است با:
[center:1df9153247]
من این راه رو رفتم چون می دونستم که بازگشتی قبول نمی کنن. ولی راه شما هم کاملا درسته. تو کتاب با یه سری محاسبات دیگه به همین رسیده بود و بعد ساده کرده بود. (البته توضیح داده بود که ساده کردنش مهم نیست به همین دلیل من هم ساده نمی کنم!!)
