سوال نظریه اعداد حرفه ای
- شروع کننده موضوع mohamadreza salehi
- تاریخ شروع
- برچسپ ها irysc.com اثبات اعداد اعداد صحیح ترجمه سوال متغیر محمد شریفی مربع معادله نظریه اعداد کتاب
پاسخ : سوال نظریه اعداد حرفه ای
خوب اقای
mohamadreza salehi
بگید مشکل حل کجاس که تا بگم کجا اشتباه کردید:53:
خوب اقای
mohamadreza salehi
بگید مشکل حل کجاس که تا بگم کجا اشتباه کردید:53:
پاسخ : سوال نظریه اعداد حرفه ای
پس یعنی داری میگی تنها حالتی که ب.م.م برابر 1 میشه وقتیه که یکی از متغیر هامون برابر 1 باشه؟ پس این مورد هم باید اثبات بشه که نشده.
خوب باید میگفت کهx, yمخالف یک باشند و اون حالت رو چک میکرد. این مثال نقض نیست بلکه راه حل Ayfar ناقصه و شما کاملش کردید:53:
پاسخ : سوال نظریه اعداد حرفه ای
فرض كنيد x>y

و

حالا

پس داريم
 (1)
(1)
و باید دلتای معاله مربع کامل باشد پس
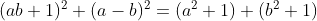
پس باید داشته باشیم

خب الآن این دو تا معادله پل هستن
((مراجعه به صفحه 106 کتاب معادلات دیوفانتی تیتو آندرسکو ترجمه محمد شریفی ))

و همچنین میتوان

را به این گونه نوشت
به طوری که برای

به جای توان
n
توان
i
میباشد
و طبق معادله درجه دوم(1) بالا
Xبه دست میاید

که به دلیل اینکه زوجیت
a,b
برابر است پس زوجیت
n,i
برابر است پس
به وضوح
X
مربع کامل میشود.
فرض كنيد x>y
و
حالا
پس داريم
و باید دلتای معاله مربع کامل باشد پس
پس باید داشته باشیم
خب الآن این دو تا معادله پل هستن
((مراجعه به صفحه 106 کتاب معادلات دیوفانتی تیتو آندرسکو ترجمه محمد شریفی ))
و همچنین میتوان
را به این گونه نوشت
به طوری که برای
به جای توان
n
توان
i
میباشد
و طبق معادله درجه دوم(1) بالا
Xبه دست میاید
که به دلیل اینکه زوجیت
a,b
برابر است پس زوجیت
n,i
برابر است پس
به وضوح
X
مربع کامل میشود.
آخرین ویرایش توسط مدیر
