سوال گراف خیلی قشنگ
- ارسال ها
- 327
- لایک ها
- 378
- امتیاز
- 0
پاسخ : سوال گراف خیلی قشنگ
حالا که ایده لو رفت من راه خودمو میذارم(البته راه من دقیقا راهیه که کتاب منبع رفته.پس در واقع میشه گفت اول راه کتاب بوده بعدش راه من :4
:
از برهان خلف استفاده میکنیم.فرض کنید گراف هیچ دوری به طول 4 نداشته باشد.تعداد جفت های متمایز راس ها را به دو طریق می شماریم.از یک طرف این تعداد برابرست با
.
از طرف دیگر فرض کنید
)
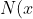مجموعه راس های همسایه x باشد.واضح است که به ازای هر دو راس دلخواه x,y داریم
\cap N(y)|\leq 1)
.چون اگه اینطور نباشه با دو راس از همسایه های x,y و خود x,y یک دور 4 تایی بوجود میاد.حال به ازای هر راس دلخواهی مانند x تعداد جفت راس های همسایه x برابر است با
}{2}=\binom{d(x)}{2})
و از اونجا که هیچ دو راسی بیش از یه همسایه مشترک ندارن، پس تعداد جفت راس های متمایز این گراف حداقل برابره با
}\binom{d(x)}{2})
. پس داریم:
}\binom{d(x)}{2}\leq \binom{n}{2})
}\binom{d(x)}{2}\geq n\binom{\frac{2m}{n}}{2}\Rightarrow \binom{n}{2}\geq \frac{m(2m-n)}{n}\Rightarrow 2m^2-nm-\frac{n^2(n-1)}{2}\leq 0\Rightarrow m\leq \frac{n+\sqrt{n^2+4n^2(n-1)}}{4}=\frac{n}{4}(1+\sqrt{4n-3}))
حالا که ایده لو رفت من راه خودمو میذارم(البته راه من دقیقا راهیه که کتاب منبع رفته.پس در واقع میشه گفت اول راه کتاب بوده بعدش راه من :4
:از برهان خلف استفاده میکنیم.فرض کنید گراف هیچ دوری به طول 4 نداشته باشد.تعداد جفت های متمایز راس ها را به دو طریق می شماریم.از یک طرف این تعداد برابرست با
از طرف دیگر فرض کنید
حالا با توجه به نامساوی ینسن در توابع محدب داریم(bgo جان توجه کن:4 :
:که خلاف فرض مساله است.پس گراف دوری به طول 4 دارد....
P.S. اگه قسمتی از راه حل واضح نبود،بگید تا توضیح بدم... :3:
P.S. اگه قسمتی از راه حل واضح نبود،بگید تا توضیح بدم... :3:
پاسخ : سوال گراف خیلی قشنگ
اون چون انتخاب دو از mه دیگه نمیخواد لازم نیس اما برای k های بیشتر لازمه فک کنم
اما از طرفی هم میتونیم تابع رو جبری تعریف کنیم و دیگه نمیخواد اونو اثبات کنی راه حل tstایران 2008 رو که بری ببینی امید حاتمی سوال 799 تیم رو چطور با ین سن تعمیم یافته حل کرده و اونم اثبات نکرده.
یه نکته ای رو من متوجهش شدم....... من توی اثباتم ثابت نکردم که
.ولی طبق این چیزی که شما اینجا گفتین باید ثابت میکردم....شما ایده ای دارید که چرا
؟
اما از طرفی هم میتونیم تابع رو جبری تعریف کنیم و دیگه نمیخواد اونو اثبات کنی راه حل tstایران 2008 رو که بری ببینی امید حاتمی سوال 799 تیم رو چطور با ین سن تعمیم یافته حل کرده و اونم اثبات نکرده.