دوستان شركت كننده در مرحله ي دوم المپياد رياضي، مي تونند جواب ها و نظراتشون رو در مورد سوال 2 در اين تاپيك مطرح كنند. (لطفا بحث هاي حاشيه اي رو در اين تاپيك مطرح نكنيد و فقط به لحاظ فني روي اين سوال بحث كنيد. درضمن لطف كنيد قبل از برگزاري آزمون، در اين تاپيك چيزي ننويسيد.)
نقطه در صفحه داریم که هیچ سه تایی از آن ها بر روی یک خط نیستند. ثابت کنید تعداد مثلث هایی که رئوس آن ها از بین این
نقطه باشند و مساحت آن ها 1 باشد، از
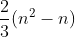بیش تز نیست.
مرحله ي دوم المپياد رياضي سال 89-88 (سوال 2)
- ارسال ها
- 4
- لایک ها
- 0
- امتیاز
- 0
سوال2
سلام.كسي اين سوالا با استقرا حل كرده؟آخه من با استقرا حل كردم ولي جوب فك كنم زياد داره مي شه يكي با استقرا حل كنه؟؟
يعني اصلا مي شه گفت يه راسي تو n+1هست كه تعداد مثلث هايي كه تشكيل ميده حداكثر برابر 4/3nاست وان را حذف مي كنيم.حالا يايد ثابت كنيم كه چنين راسي وجود دارد؟
آيا اين درسته؟/؟
مي دونم راه حل اسون تري داره ولي سر امتحان به ذهنم نرسيد؟
و اگه در سته مي شه كاملش كنيد.ممنونسوال 2
سلام.كسي اين سوالا با استقرا حل كرده؟آخه من با استقرا حل كردم ولي جوب فك كنم زياد داره مي شه يكي با استقرا حل كنه؟؟
يعني اصلا مي شه گفت يه راسي تو n+1هست كه تعداد مثلث هايي كه تشكيل ميده حداكثر برابر 4/3nاست وان را حذف مي كنيم.حالا يايد ثابت كنيم كه چنين راسي وجود دارد؟
آيا اين درسته؟/؟
مي دونم راه حل اسون تري داره ولي سر امتحان به ذهنم نرسيد؟
و اگه در سته مي شه كاملش كنيد.ممنونسوال 2
- ارسال ها
- 4
- لایک ها
- 0
- امتیاز
- 0
هر دو نقطه را که از این n نقطه در نظر بگیریم و خط بین این دو را رسم کنیم دو خط مثل d , l وجود دارند که هر نقطه روی این دو خط با آن دونقطه مثلثی به مساحت یک تشکیل میدهند. چون هیچ سه نقطه ای روی یک خط نیستند پس روی d حداکثر دو نقطه و روی l هم حداکثر دو نقطه با این خاصیت وجود دارد.حالا تعداد حالت های انتخاب دو نقطه از این n نقطه را در 4 ضرب میکنیم و چون هرمثلث را سه بار شمرده ایم عبارت را بر 3 تقسیم می کنیم که همان جواب اصلی به دست می آید.
Re: سوال2
بعيد مي دانم اين سوال با استقرا حل شود! از آن تيپ سوال‌هايي نيست كه به آن استقرا بخورد. تازه اگر مي خواست استقرا بخورد منطقي بود كه از n به n+3 استقرا بزنيد. به هر حال مي توان نقطه اي را در نظر گرفت كه در حداكثر 2n-4 مثلث قرار داشته باشد.
راستي شنيدم قرار است تلافي امروز را فردا سرتان در بياورند! ظاهرا تعداد كساني كه 3 سوال را كامل حل كردند زياد است از اصفهان و تهران كه آمار سنگيني مي رسد. آمار مشهد هم به زودي در مي آيد.
بعيد مي دانم اين سوال با استقرا حل شود! از آن تيپ سوال‌هايي نيست كه به آن استقرا بخورد. تازه اگر مي خواست استقرا بخورد منطقي بود كه از n به n+3 استقرا بزنيد. به هر حال مي توان نقطه اي را در نظر گرفت كه در حداكثر 2n-4 مثلث قرار داشته باشد.
راستي شنيدم قرار است تلافي امروز را فردا سرتان در بياورند! ظاهرا تعداد كساني كه 3 سوال را كامل حل كردند زياد است از اصفهان و تهران كه آمار سنگيني مي رسد. آمار مشهد هم به زودي در مي آيد.
mrbayat گفت
هر دو نقطه را که از این n نقطه در نظر بگیریم و خط بین این دو را رسم کنیم دو خط مثل d , l وجود دارند که هر نقطه روی این دو خط با آن دونقطه مثلثی به مساحت یک تشکیل میدهند. چون هیچ سه نقطه ای روی یک خط نیستند پس روی d حداکثر دو نقطه و روی l هم حداکثر دو نقطه با این خاصیت وجود دارد.حالا تعداد حالت های انتخاب دو نقطه از این n نقطه را در 4 ضرب میکنیم و چون هرمثلث را سه بار شمرده ایم عبارت را بر 3 تقسیم می کنیم که همان جواب اصلی به دست می آید.
- ارسال ها
- 4
- لایک ها
- 0
- امتیاز
- 0
سلام.مي شه به اين سوالم جواب بديد..ولي براي سوال 2 استقرا زدم راه حل ديگه اش را مي دونم ولي مي خوام بدونم استقرام درسته؟البته به احتمال زياد غلطه.
ادعا مي كنم كه راسي وجود دارد كه تعداد مثلث هاييي ه مي سازد حداكثر برابر 4/3n در n+1راس هست كه ما ان را ناديده مي گيريم و طبق فرض مساله حله.
حالا بايد ثابت كنيم چنين راسي وجود دارد كه اينجا براي n<=9 ثابت كردم اگر اين طوري نباشد تعداد مثلث ها به مساحت 1 تعدادشون از تعداد كل مثلث ها به هر مساحتي بيشتره.تناقض.
پس براي n<=9ثابت شد چنين راسي وجود دارد.
بازم استقرا زدو و حالت پايه ام را اين n<=9
گرفتم و ازn بهn+7رسيدم. يعني بايد ثابت كنيم كه درn+7 تا راسي وجود دارد كه كه حداكثر 4/3(n+5)تا مثلث مي سازد.براي اين قسمت منظورمه كه چرت نوشتم.يعني گفتم كه در بين n+7راس يك 7تايي و جود دارد كه حداكثر 9 تا مثلث بسازد كه ماآنرا در نظر نميگيريم و مساله حله.
براي اثبات وجود چنين 7تايي هم گفتم اگه وجود نداشته باشه پس هر 7تايي حداقل 10 تا مثلث مي سازد كه اين تناقض است.
ادعا مي كنم كه راسي وجود دارد كه تعداد مثلث هاييي ه مي سازد حداكثر برابر 4/3n در n+1راس هست كه ما ان را ناديده مي گيريم و طبق فرض مساله حله.
حالا بايد ثابت كنيم چنين راسي وجود دارد كه اينجا براي n<=9 ثابت كردم اگر اين طوري نباشد تعداد مثلث ها به مساحت 1 تعدادشون از تعداد كل مثلث ها به هر مساحتي بيشتره.تناقض.
پس براي n<=9ثابت شد چنين راسي وجود دارد.
بازم استقرا زدو و حالت پايه ام را اين n<=9
گرفتم و ازn بهn+7رسيدم. يعني بايد ثابت كنيم كه درn+7 تا راسي وجود دارد كه كه حداكثر 4/3(n+5)تا مثلث مي سازد.براي اين قسمت منظورمه كه چرت نوشتم.يعني گفتم كه در بين n+7راس يك 7تايي و جود دارد كه حداكثر 9 تا مثلث بسازد كه ماآنرا در نظر نميگيريم و مساله حله.
براي اثبات وجود چنين 7تايي هم گفتم اگه وجود نداشته باشه پس هر 7تايي حداقل 10 تا مثلث مي سازد كه اين تناقض است.