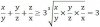مکعب کامل

[M_Sharifi]

یه سوال:
فرض کنید

اعدادی صحیح اند که

. ثابت کنید

مکعب کامل است.

 

[MesiGooly]

از نامساوي حسابي-هندسي مي دانيم كه:

وحالت تساوي زماني است كه
x/y=y/z=z/x
كه نتيجه مي دهد.x=y=z
پس
xyz=x^3

 

[M_Sharifi]

ولی سوال نگفته که x,y,z اعداد مثبتی اند. بنابراین نمیشه از نابرابری میانگین حسابی- هندسی استفاده کرد.

 

[seifi_seifi]

فرض کنید p عامل اولی به غیر از 3 از a و b و c باشد و a=p[SUP]x[/SUP]×q و b=p[SUP]y[/SUP]×r و c=p[SUP]z[/SUP]×s که q,r,s نسبت به p اولند.

حال فرض کنید x>=y>=z حال باید (a[SUP]2[/SUP]c+b[SUP]2[/SUP]a+c[SUP]2[/SUP]b) بر abc بخشپذیر باشد و خارج قسمت این تقسیم عامل p را نداشته باشد.

پس باید یا 2z+y=x+y+z باشد و یا اینکه 2z+y=2y+x باشد که از حالت اول بدست میاید z=x که از این هم بدست میاید x=y=z (با توجه

به نامساوی بین x,y,z) پس x+y+z=3x واز حالت دوم بدست میاید 2z=x+y پس x+y+z=3z پس در هر دو حال توان p در xyz مضرب 3

است.

حال اگر p=3 باشد.این بار باید در خارج قسمت تقسیم بالا فقط یک عامل 3 داشته باشیم پس یا 2z+y=x+y+z+1 و یا 2z+y=2y+x حالت

اول که امکان ندارد زیرا z=x+1 و حالت دوم هم نتیجه میدهد x+y+z=3z

پس در کل abc مکعب کامل است.

 

[M_Sharifi]

یه راه حل دیگه:
فرض کنید

. در این صورت

ریشه های معادله ی

[center:4cf59abf5a]

[/center:4cf59abf5a]اند که

. از این معادله نتیجه می گیریم
[center:4cf59abf5a]

از تقسیم این رابطه به ازای

نتیجه می گیریم​

[/center:4cf59abf5a][center:4cf59abf5a]

درنتیجه

. پس

مکعب عددی گویا و نتیجتا مکعب عددی صحیح است.​

[/center:4cf59abf5a]