x^4 + 4^x = p
C
Olympiad گفت
براي اينكه
 عددي اول باشد (به غير از 2) بديهي است كه
عددي اول باشد (به غير از 2) بديهي است كه
 بايد فرد باشد. حال ما دو طرف تساوي را به پيمانه ي 5 در نظر مي گيريم. ميدانيم كه
بايد فرد باشد. حال ما دو طرف تساوي را به پيمانه ي 5 در نظر مي گيريم. ميدانيم كه

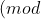

اما چون
 عددي فرد* مي باشد ، فقط
عددي فرد* مي باشد ، فقط

 و همچنين چون
و همچنين چون
 عددي فرد است ميدانيم:
عددي فرد است ميدانيم:

 بنابراين بر 5 بخشپذير مي شود.
بنابراين بر 5 بخشپذير مي شود.
پس
 فقط عدد 5 مي تواند باشد كه آن هم به ازاي
فقط عدد 5 مي تواند باشد كه آن هم به ازاي
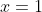 مي باشد.
مي باشد.
اما چون
پس
نکته ای که هیچکس به آن توجه نکرد:
پس چنین عددی وجود ندارد.
vasebad گفت
Olympiad گفت
براي اينكه
 عددي اول باشد (به غير از 2) بديهي است كه
عددي اول باشد (به غير از 2) بديهي است كه
 بايد فرد باشد. حال ما دو طرف تساوي را به پيمانه ي 5 در نظر مي گيريم. ميدانيم كه
بايد فرد باشد. حال ما دو طرف تساوي را به پيمانه ي 5 در نظر مي گيريم. ميدانيم كه

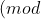

اما چون
 عددي فرد* مي باشد ، فقط
عددي فرد* مي باشد ، فقط

 و همچنين چون
و همچنين چون
 عددي فرد است ميدانيم:
عددي فرد است ميدانيم:

 بنابراين بر 5 بخشپذير مي شود.
بنابراين بر 5 بخشپذير مي شود.
پس
 فقط عدد 5 مي تواند باشد كه آن هم به ازاي
فقط عدد 5 مي تواند باشد كه آن هم به ازاي
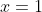 مي باشد.
مي باشد.
اما چون
پس
نکته ای که هیچکس به آن توجه نکرد:
پس چنین عددی وجود ندارد.
C
Olympiad گفت
vasebad گفت
Olympiad گفت
براي اينكه
 عددي اول باشد (به غير از 2) بديهي است كه
عددي اول باشد (به غير از 2) بديهي است كه
 بايد فرد باشد. حال ما دو طرف تساوي را به پيمانه ي 5 در نظر مي گيريم. ميدانيم كه
بايد فرد باشد. حال ما دو طرف تساوي را به پيمانه ي 5 در نظر مي گيريم. ميدانيم كه

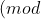

اما چون
 عددي فرد* مي باشد ، فقط
عددي فرد* مي باشد ، فقط

 و همچنين چون
و همچنين چون
 عددي فرد است ميدانيم:
عددي فرد است ميدانيم:

 بنابراين بر 5 بخشپذير مي شود.
بنابراين بر 5 بخشپذير مي شود.
پس
 فقط عدد 5 مي تواند باشد كه آن هم به ازاي
فقط عدد 5 مي تواند باشد كه آن هم به ازاي
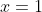 مي باشد.
مي باشد.
اما چون
پس
نکته ای که هیچکس به آن توجه نکرد:
پس چنین عددی وجود ندارد.
vasebad گفت
Olympiad گفت
vasebad گفت
Olympiad گفت
براي اينكه
 عددي اول باشد (به غير از 2) بديهي است كه
عددي اول باشد (به غير از 2) بديهي است كه
 بايد فرد باشد. حال ما دو طرف تساوي را به پيمانه ي 5 در نظر مي گيريم. ميدانيم كه
بايد فرد باشد. حال ما دو طرف تساوي را به پيمانه ي 5 در نظر مي گيريم. ميدانيم كه

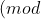

اما چون
 عددي فرد* مي باشد ، فقط
عددي فرد* مي باشد ، فقط

 و همچنين چون
و همچنين چون
 عددي فرد است ميدانيم:
عددي فرد است ميدانيم:

 بنابراين بر 5 بخشپذير مي شود.
بنابراين بر 5 بخشپذير مي شود.
پس
 فقط عدد 5 مي تواند باشد كه آن هم به ازاي
فقط عدد 5 مي تواند باشد كه آن هم به ازاي
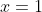 مي باشد.
مي باشد.
اما چون
پس
نکته ای که هیچکس به آن توجه نکرد:
پس چنین عددی وجود ندارد.
يعني حالتي كه x بر 5 بخشپذير است (x=10t+5)
