یافتن مقداری برای عبارت خواسته شده،
- ارسال ها
- 2,708
- لایک ها
- 3,152
- امتیاز
- 0
پاسخ : از بین بردن شک
جزو قوانین سایته اگه نام تایپیکی مناسب نبود بهش جواب ندیم. دو سه مورد جوابتون داده شد البته!
وقتی نام نامناسبه خیلی از بچه ها متوجه نمیشن تایپیک به رشتشون ربط داره و اونو نمیخونن.
و از طرفی وقتی تو انجمن جستجو میکنیم مثلا در مورد عناصر واسطه تایپیکی که شما گذاشته بودید بدلیل نام نامناسب پیدا نمیشه.
انتخاب نام مناسب زحمتی نداره. داره>؟؟
جزو قوانین سایته اگه نام تایپیکی مناسب نبود بهش جواب ندیم. دو سه مورد جوابتون داده شد البته!
وقتی نام نامناسبه خیلی از بچه ها متوجه نمیشن تایپیک به رشتشون ربط داره و اونو نمیخونن.
و از طرفی وقتی تو انجمن جستجو میکنیم مثلا در مورد عناصر واسطه تایپیکی که شما گذاشته بودید بدلیل نام نامناسب پیدا نمیشه.
انتخاب نام مناسب زحمتی نداره. داره>؟؟
پاسخ : یافتن مقداری برای عبارت خواسته شده،
اگر اشتباه نکنم داریم:

در حالت کلی، یک رابطه ی بازگشتی بین چند جمله ای های متقارن برقرار است.
اتحاد های مجموع نیوتون:
فرض کنید
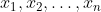 اعدادی در میدان دلخواه
اعدادی در میدان دلخواه
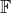 باشند.
باشند.
اگر
) ،
،
 امین مجموع متقارن از متغیر های
امین مجموع متقارن از متغیر های
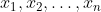 باشد و
باشد و
=x_1^k+x_2^k+\dots+x_n^k)
آنگاه رابطه های بازگشتی زیر بر قرار است:
(برای اختصار، تنها از نماد های
 و
و
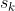 استفاده می کنیم. برای
استفاده می کنیم. برای
 تعریف می کنیم:
تعریف می کنیم:
 )
)




^{k-1}k\sigma_k)
* احتمالا به جای میدان بتوان هر گروه آبلی را جای گذاری نمود.
** با استفاده از این روابط بازگشتی می توان به راحتی مساله ی بالا را حل نمود.
***
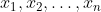 ریشه های چند جمله ای
ریشه های چند جمله ای
=x^n-\sigma_1x^{n-1}+\dots+(-1)^n\sigma_n)
**** یکی از ساده ترین اثبات های این قضیه با استفاده از استقرای قوی است. ولی به دلیل سنگین بودن نمادگزاری ها از ذکر اثبات فعلا خود داری می کنم.
*****می توان با استفاده از تابع مولد و استفاده از تکنیک ضرب کانولوشن نیز این قضیه را ثابت نمود.
****** خودم هم یه اثبات نصفه ای با استفاده از مشتق جزئی دارم.
اگر اشتباه نکنم داریم:
در حالت کلی، یک رابطه ی بازگشتی بین چند جمله ای های متقارن برقرار است.
اتحاد های مجموع نیوتون:
فرض کنید
اگر
آنگاه رابطه های بازگشتی زیر بر قرار است:
(برای اختصار، تنها از نماد های
* احتمالا به جای میدان بتوان هر گروه آبلی را جای گذاری نمود.
** با استفاده از این روابط بازگشتی می توان به راحتی مساله ی بالا را حل نمود.
***
**** یکی از ساده ترین اثبات های این قضیه با استفاده از استقرای قوی است. ولی به دلیل سنگین بودن نمادگزاری ها از ذکر اثبات فعلا خود داری می کنم.
*****می توان با استفاده از تابع مولد و استفاده از تکنیک ضرب کانولوشن نیز این قضیه را ثابت نمود.
****** خودم هم یه اثبات نصفه ای با استفاده از مشتق جزئی دارم.
