سهمی های غیر متقاطع
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : سهمی های غیر متقاطع
اینم یک عکس خوب
http://up.vatandownload.com/images/abkj74egjirbn4q6zcui.png
اینم یک عکس خوب
http://up.vatandownload.com/images/abkj74egjirbn4q6zcui.png
آخرین ویرایش توسط مدیر
پاسخ : سهمی های غیر متقاطع
توی شکلی که کشیدید هیچ خطی وجود نداره که هیچ کدوم از سهمی ها رو قطع نکنه؟ (مثلا y=-1)
شرطش هم ساده است..هیچ نقطه ای از سهمی نباید تو صفحه بالا(داخل) سهمی اول باشه..وگرنه نمیشه اون خط رو کشید..
اینم یک عکس خوب
http://up.vatandownload.com/images/abkj74egjirbn4q6zcui.png
اینم یک عکس خوب
http://up.vatandownload.com/images/abkj74egjirbn4q6zcui.png
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : سهمی های غیر متقاطع
سعی کردم ثابت کنم که نمیشه..دو تا معادله سهمی و یک معادله خط نوشتم...برای هر کدوم از سهمی ها یک شرط از دلتای معادله داریم...
هر دوتاش اگر برقرار باشه>>همیشه میشه اون خطه رو کشید!
ولی یک حالت خاصی چیزی باید داشته باشه..
بلخره سوال آقای شریفیه دیگه!
این که قطع میکنه.راست میگی...
هر دوتاش اگر برقرار باشه>>همیشه میشه اون خطه رو کشید!
ولی یک حالت خاصی چیزی باید داشته باشه..
بلخره سوال آقای شریفیه دیگه!
پاسخ : سهمی های غیر متقاطع
باید دقت کنی که دو تا سهمی ای که داریم لزوما محور تقارنشون موازی با هم نیست که بتونی به راحتی با دلتا سوال رو جلو ببری.باید بررسی کنیم ببینیم محور تقارن دو تا سهمی چه زاویه هایی می تونند با هم بسازند.
پس باید از معادله کلی سهمی یا حتی ماتریس دوران استفاده کنیم.
سعی کردم ثابت کنم که نمیشه..دو تا معادله سهمی و یک معادله خط نوشتم...برای هر کدوم از سهمی ها یک شرط از دلتای معادله داریم...
هر دوتاش اگر برقرار باشه>>همیشه میشه اون خطه رو کشید!
ولی یک حالت خاصی چیزی باید داشته باشه..
بلخره سوال آقای شریفیه دیگه!
هر دوتاش اگر برقرار باشه>>همیشه میشه اون خطه رو کشید!
ولی یک حالت خاصی چیزی باید داشته باشه..
بلخره سوال آقای شریفیه دیگه!
باید دقت کنی که دو تا سهمی ای که داریم لزوما محور تقارنشون موازی با هم نیست که بتونی به راحتی با دلتا سوال رو جلو ببری.باید بررسی کنیم ببینیم محور تقارن دو تا سهمی چه زاویه هایی می تونند با هم بسازند.
پس باید از معادله کلی سهمی یا حتی ماتریس دوران استفاده کنیم.
پاسخ : سهمی های غیر متقاطع
جواب اینه که همواره چنین خطی وجود داره. در واقع حالت کلی تر اینه که اگر محور های دو سهمی موازی نباشن بدون توجه به متقاطع بودن یا نبودن میشه چنین خطی رسم کرد.
اثباتشم کاملا جبریه: فرض خلف: فرض کنید هر خطی حداقل یکی از دوتا سهمی رو قطع کنه.
محور های مختصات رو طوری انتخاب می کنیم که معادله ی سهمی اول به صورت
 باشه (که a>0). حالا تمام خط هایی رو پیدا می کنیم که با این سهمی برخورد نمی کنن. اگه خطمون
باشه (که a>0). حالا تمام خط هایی رو پیدا می کنیم که با این سهمی برخورد نمی کنن. اگه خطمون
 باشه باید دلتای
باشه باید دلتای
 کوچکتر از 0 باشه پس نمودارشون متقاطع نیست اگر و فقط اگر
کوچکتر از 0 باشه پس نمودارشون متقاطع نیست اگر و فقط اگر
 .
.
حالا محور ها رو حول مبدا به اندازه
 پادساعتگرد دوران میدیم تا محور سهمی دوم موازی محور y جدید باشه. معادله ی خط
پادساعتگرد دوران میدیم تا محور سهمی دوم موازی محور y جدید باشه. معادله ی خط
 رو که
رو که
 در مختصات جدید به دست میاریم.
در مختصات جدید به دست میاریم.
از این نکته استفاده می کنیم که اگر مختصات نقطه ی
 با دوران محورها به
با دوران محورها به
 تبدیل بشه: (فکر کنم توی توماس هست)
تبدیل بشه: (فکر کنم توی توماس هست)

اگه این ها رو توی معادله خط جاگذاری کنیم به دست میاد:

که

فرض کنید معادله ی سهمی (دوم) دوران یافته برابر
 باشه(s>0). طبق فرض خلفمون و اینکه هیچ یک از خطوط (1) سهمی اول رو قطع نمی کنه پس هر یک از این خطوط با سهمی دوم برخورد داره. پس معادله ی زیر حداقل یک جواب حقیقی داره:
باشه(s>0). طبق فرض خلفمون و اینکه هیچ یک از خطوط (1) سهمی اول رو قطع نمی کنه پس هر یک از این خطوط با سهمی دوم برخورد داره. پس معادله ی زیر حداقل یک جواب حقیقی داره:
 پس دلتاش نامنفیه:
پس دلتاش نامنفیه:
 m حقیقی دلخواه بود؛ پس اگر m ای وجود داشته باشه که مخرج کسرها یعنی
m حقیقی دلخواه بود؛ پس اگر m ای وجود داشته باشه که مخرج کسرها یعنی
 مثبت بشه، اونوقت چون d فقط از بالا کران داره میتونیم d رو بزرگ و منفی در نظر بگیریم و دلتا منفی میشه... تناقض!
مثبت بشه، اونوقت چون d فقط از بالا کران داره میتونیم d رو بزرگ و منفی در نظر بگیریم و دلتا منفی میشه... تناقض!
پس چنین m ای وجود نداره و همواره
 . خیلی راحت میتونید ببینید اگر
. خیلی راحت میتونید ببینید اگر
 میشه m رو به قدری بزرگ (منفی یا مثبت) در نظر گرفت که عبارت برقرار نباشه. پس
میشه m رو به قدری بزرگ (منفی یا مثبت) در نظر گرفت که عبارت برقرار نباشه. پس
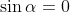 و
و
 پس دورانمون 180 درجه هست.
پس دورانمون 180 درجه هست.
بنابراین میتونیم فرض کنیم معادله ی دو سهمی به صورت
 است. این حالت هم خیلی ساده تره، میتونید مثل بالا خطوطی که با سهمی اول برخورد نمیکنن به دست بیارید و چون همه با دومی برخورد دارن، نتیجه بگیرید دو سهمی متقاطع اند.
است. این حالت هم خیلی ساده تره، میتونید مثل بالا خطوطی که با سهمی اول برخورد نمیکنن به دست بیارید و چون همه با دومی برخورد دارن، نتیجه بگیرید دو سهمی متقاطع اند.
جواب اینه که همواره چنین خطی وجود داره. در واقع حالت کلی تر اینه که اگر محور های دو سهمی موازی نباشن بدون توجه به متقاطع بودن یا نبودن میشه چنین خطی رسم کرد.
اثباتشم کاملا جبریه: فرض خلف: فرض کنید هر خطی حداقل یکی از دوتا سهمی رو قطع کنه.
محور های مختصات رو طوری انتخاب می کنیم که معادله ی سهمی اول به صورت
حالا محور ها رو حول مبدا به اندازه
از این نکته استفاده می کنیم که اگر مختصات نقطه ی
که
پس چنین m ای وجود نداره و همواره
بنابراین میتونیم فرض کنیم معادله ی دو سهمی به صورت
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : سهمی های غیر متقاطع
فقط یک چیزی رو در نظر نگرفتی...
این سوال آقای شریفیه!!
حتمن یک نکته دیگه داره.
جواب اینه که همواره چنین خطی وجود داره. در واقع حالت کلی تر اینه که اگر محور های دو سهمی موازی نباشن بدون توجه به متقاطع بودن یا نبودن میشه چنین خطی رسم کرد.
اثباتشم کاملا جبریه: فرض خلف: فرض کنید هر خطی حداقل یکی از دوتا سهمی رو قطع کنه.
محور های مختصات رو طوری انتخاب می کنیم که معادله ی سهمی اول به صورت
 باشه (که a>0). حالا تمام خط هایی رو پیدا می کنیم که با این سهمی برخورد نمی کنن. اگه خطمون
باشه (که a>0). حالا تمام خط هایی رو پیدا می کنیم که با این سهمی برخورد نمی کنن. اگه خطمون
 باشه باید دلتای
باشه باید دلتای
 کوچکتر از 0 باشه پس نمودارشون متقاطع نیست اگر و فقط اگر
کوچکتر از 0 باشه پس نمودارشون متقاطع نیست اگر و فقط اگر
 .
.
حالا محور ها رو حول مبدا به اندازه
 پادساعتگرد دوران میدیم تا محور سهمی دوم موازی محور y جدید باشه. معادله ی خط
پادساعتگرد دوران میدیم تا محور سهمی دوم موازی محور y جدید باشه. معادله ی خط
 رو که
رو که
 در مختصات جدید به دست میاریم.
در مختصات جدید به دست میاریم.
از این نکته استفاده می کنیم که اگر مختصات نقطه ی
 با دوران محورها به
با دوران محورها به
 تبدیل بشه: (فکر کنم توی توماس هست)
تبدیل بشه: (فکر کنم توی توماس هست)

اگه این ها رو توی معادله خط جاگذاری کنیم به دست میاد:

که

فرض کنید معادله ی سهمی (دوم) دوران یافته برابر
 باشه(s>0). طبق فرض خلفمون و اینکه هیچ یک از خطوط (1) سهمی اول رو قطع نمی کنه پس هر یک از این خطوط با سهمی دوم برخورد داره. پس معادله ی زیر حداقل یک جواب حقیقی داره:
باشه(s>0). طبق فرض خلفمون و اینکه هیچ یک از خطوط (1) سهمی اول رو قطع نمی کنه پس هر یک از این خطوط با سهمی دوم برخورد داره. پس معادله ی زیر حداقل یک جواب حقیقی داره:
 پس دلتاش نامنفیه:
پس دلتاش نامنفیه:
 m حقیقی دلخواه بود؛ پس اگر m ای وجود داشته باشه که مخرج کسرها یعنی
m حقیقی دلخواه بود؛ پس اگر m ای وجود داشته باشه که مخرج کسرها یعنی
 مثبت بشه، اونوقت چون d فقط از بالا کران داره میتونیم d رو بزرگ و منفی در نظر بگیریم و دلتا منفی میشه... تناقض!
مثبت بشه، اونوقت چون d فقط از بالا کران داره میتونیم d رو بزرگ و منفی در نظر بگیریم و دلتا منفی میشه... تناقض!
پس چنین m ای وجود نداره و همواره
 . خیلی راحت میتونید ببینید اگر
. خیلی راحت میتونید ببینید اگر
 میشه m رو به قدری بزرگ (منفی یا مثبت) در نظر گرفت که عبارت برقرار نباشه. پس
میشه m رو به قدری بزرگ (منفی یا مثبت) در نظر گرفت که عبارت برقرار نباشه. پس
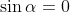 و
و
 پس دورانمون 180 درجه هست.
پس دورانمون 180 درجه هست.
بنابراین میتونیم فرض کنیم معادله ی دو سهمی به صورت
 است. این حالت هم خیلی ساده تره، میتونید مثل بالا خطوطی که با سهمی اول برخورد نمیکنن به دست بیارید و چون همه با دومی برخورد دارن، نتیجه بگیرید دو سهمی متقاطع اند.
است. این حالت هم خیلی ساده تره، میتونید مثل بالا خطوطی که با سهمی اول برخورد نمیکنن به دست بیارید و چون همه با دومی برخورد دارن، نتیجه بگیرید دو سهمی متقاطع اند.
اثباتشم کاملا جبریه: فرض خلف: فرض کنید هر خطی حداقل یکی از دوتا سهمی رو قطع کنه.
محور های مختصات رو طوری انتخاب می کنیم که معادله ی سهمی اول به صورت
حالا محور ها رو حول مبدا به اندازه
از این نکته استفاده می کنیم که اگر مختصات نقطه ی
که
پس چنین m ای وجود نداره و همواره
بنابراین میتونیم فرض کنیم معادله ی دو سهمی به صورت
این سوال آقای شریفیه!!
حتمن یک نکته دیگه داره.
