n ضلعی محدب

[math-sina]

در یک n ضلعی محدب، n+1 قطر رسم شده است.
ثابت کنید 2 قطر وجود دارند به طوری که با هم اشتراک ندارند (هیچ برخوردی با هم ندارند)

 

[Aref]

پاسخ : n ضلعی محدب

بدون کاستن از کلیت مساله فرض کنید که n ضلعی، منتظم است. اعداد 0 تا n-1 را را با همین ترتیب به رئوس نسبت دهید.
به راحتی مشاهده می شود که دو قطر که در دو راس آنها به ترتیب جفت عدد های

نوشته شده است موازیند اگر و فقط اگر:

.
بقیش راحته.

 

[mahanmath]

پاسخ : n ضلعی محدب

خوب مثل اینکه از اون راهی‌ که بهت گفتم خوشت نیومد ... مشکلی‌ نیست ، اینم یه راه دیگه :3::
برای هر راس یه خط گذرنده ازش رو در نظر بگیر که همه یال‌های اخراج شده از اون راس تو یه نیم صفحه تعیین شده توسط این خط باشن . حالا جهت ساعت گرد رو در نظر بگیر و بین یال‌های خارجه از اون راس راست ترینشون رو حذف کن .اینکارو همزمان برای همه راس‌ها انجام می‌دیم . با این کار حداکثر

تا یال حذف کردیم ، پس باید یه یال مونده باشه.
اگه یال

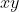مونده باشه یعنی‌ یال‌های

و

موجود بودن که از

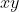چپ تر بودن (چپ تر بودن یه بار نسبت به یال‌های خارجه از

و یه بار هم نسبت به یال‌های خارجه از

) .
ولی‌ این دو تا یال نمی‌تونن همدیگرو قطع نمی‌کنن چون باید در ۲ طرف مختلف

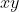واقع باشند .:95:


عارف می‌شه بیشتر راه تو توضیح بدی ؟
منظور از اینکه این ۲تا قطر همدیگرو قطع نکنند یعنی‌ پاره خط‌هاشون همدیگرو قطع نکنند نه خط‌هاشون (قطع نکردن معنی‌ موازی بودن نمیده ) .

 

[Aref]

پاسخ : n ضلعی محدب

عارف می‌شه بیشتر راه تو توضیح بدی ؟
منظور از اینکه این ۲تا قطر همدیگرو قطع نکنند یعنی‌ پاره خط‌هاشون همدیگرو قطع نکنند نه خط‌هاشون.

خب اگه دو تا قطر توی n ضلعی منتظم موازی باشند، اگه راس هارو طوری تکون بدیم که n ضلعی محدب بمونه، پاره خط هاشون همدیگرو قطع نمی کنند.:92:

 

[mimilad]

پاسخ : n ضلعی محدب

من با راه استاد ماهان حل کردم ولی یه راه دیگه هم براش پیدا کردم گفتم بنویسم :

یه راه دیگه :
به اسقرا حکم رو ثابت میکنیم برای این کار رئوس را با شماره های 1 تا n به صورت پاد ساعتگرد شماره گذاری میکنیم حالا راسی که بیشترین قطر خارج شده از خود را داره رو در نظر میگریم وفرض میکنیم این راس راس شماره یکه (به وضوح حداقل سه قطر از این راس خارج میشه ) حالا رئوسی که قطر های از راس شماره یک به ان ها میروند رو m_1 , m_2 , .......... m_k در نظر میگریم (به ترتیب ازچپ به راست به صورت پاد ساعتگرد) به وضوح هر قطر باقیمانده یکی از رئوس 2 ,3 ..........m_1 را به کی از رئوس m_k ., m_k+1 ,...........n وصل میکند همچنین به راحتی میتوان اثبات کرد که هیچ قطری وجود ندارکه دوراسش m_1 , m_k باشد حالا دو راس m_1 , m_k را بر هم منطبق میکنیم و تا یه n-m +1 ضلعی داشته باشیم که شامل n_m+2 قطر است و اگر دو قطر در n ضلعی اولیه برخورد داشته باشند در چند ضلعی جدید نیز برخورد خواهند داشت حالا بنابر فرض استقرا حکم برقار میشه .

 

[mahanmath]

پاسخ : n ضلعی محدب

خب اگه دو تا قطر توی n ضلعی منتظم موازی باشند، اگه راس هارو طوری تکون بدیم که n ضلعی محدب بمونه، پاره خط هاشون همدیگرو قطع نمی کنند.:92:

ممنون .
مساله بدون شرط محدب بودن هم درسته . یعنی‌ اگه یه گراف n راس‌ی داشته باشیم که یال هاش خط راست باشن و هر ۲ تا یال با هم تقاطع داشته باشند اون موقع تعداد یال‌ها می‌شه حداکثر n .

 

[Aref]

پاسخ : n ضلعی محدب

ممنون .
مساله بدون شرط محدب بودن هم درسته . یعنی‌ اگه یه گراف n راس‌ی داشته باشیم که یال هاش خط راست باشن و هر ۲ تا یال با هم تقاطع داشته باشند اون موقع تعداد یال‌ها می‌شه حداکثر n .

بله.
در واقع باز هم اگه اون n ضلعی منتظم رو رئوسش رو طوری حرکت بدیم که ضلع هاش همدیگرو قطع نکنن، یعنی چند ضلعی ساده بمونه، باز هم حکم درسته.