یک کره و سه رنگ
پاسخ : یک کره و سه رنگ
این سوال در واقع یه ورژن معادل از قضیه بورسوک-اولام در توپولوژی هست: Borsuk–Ulam theorem - Wikipedia, the free encyclopedia
این سوال در واقع یه ورژن معادل از قضیه بورسوک-اولام در توپولوژی هست: Borsuk–Ulam theorem - Wikipedia, the free encyclopedia
- ارسال ها
- 48
- لایک ها
- 173
- امتیاز
- 0
پاسخ : یک کره و سه رنگ
یادش بخیر! این سوال یک امتحان ثوپولوژی جبری ما بود (دوره طلا پارسال)...هی روزگار :4:
AoPS Forum - compressed set • Art of Problem Solving
من لینک دادم........از ماهان هم نمی ترسم! :3:
یادش بخیر! این سوال یک امتحان ثوپولوژی جبری ما بود (دوره طلا پارسال)...هی روزگار :4:
AoPS Forum - compressed set • Art of Problem Solving
من لینک دادم........از ماهان هم نمی ترسم! :3:
پاسخ : یک کره و سه رنگ
به به ! ما یه سوال میزاریم ! 4 تا از طلایی ها جواب میدن ! :196:
حالا یه چیزی !؟ فرض کنید یک اپسیلون کمتر از یک نیم کره رو به طور کامل یک رنگ کنیم (تو این ناحیه ی کمتر از نیم کره قطری وجود نداره ) و ناحیه ی باقی مونده رو که از یک نیم کره یک اپسیلون بیشتره به دو قسمت مساوی کنیم و با رنگ ها ی 2 و 3 رنگ کنیم ! در این صورت دیگه قطری وجود نداره که هر دو سرش یک رنگ باشن!؟ درست نمیگم؟ :7:
به به ! ما یه سوال میزاریم ! 4 تا از طلایی ها جواب میدن ! :196:
حالا یه چیزی !؟ فرض کنید یک اپسیلون کمتر از یک نیم کره رو به طور کامل یک رنگ کنیم (تو این ناحیه ی کمتر از نیم کره قطری وجود نداره ) و ناحیه ی باقی مونده رو که از یک نیم کره یک اپسیلون بیشتره به دو قسمت مساوی کنیم و با رنگ ها ی 2 و 3 رنگ کنیم ! در این صورت دیگه قطری وجود نداره که هر دو سرش یک رنگ باشن!؟ درست نمیگم؟ :7:
پاسخ : یک کره و سه رنگ
خوب من اشتباه فک کردم ، ولی منظورم رو رسوندم فک کنم ..........الان شما سوال رو در حالتی میتونید با برسوک حل کنید که بدونید مجموعه‌ها بستن (یا باز یا بسته هم کافیه البته ) اما الان ما نمی‌دونیم این درسته یا نه !
اگه هیچ شرطی نداشته باشیم ، نقاط کره رو به ۲ تایی‌های (x,-x) افراز کن ، یکی از دو تا مولفه این دست هارو به دلخواه قرمز کن ، اون یکی مولفه هم آبی کن ! یعنی با ۲ تا رنگ هم میشه یه کاری کرد که رو به رو قطری تک رنگ نداشته باشیم .
خوب من اشتباه فک کردم ، ولی منظورم رو رسوندم فک کنم ..........الان شما سوال رو در حالتی میتونید با برسوک حل کنید که بدونید مجموعه‌ها بستن (یا باز یا بسته هم کافیه البته ) اما الان ما نمی‌دونیم این درسته یا نه !
اگه هیچ شرطی نداشته باشیم ، نقاط کره رو به ۲ تایی‌های (x,-x) افراز کن ، یکی از دو تا مولفه این دست هارو به دلخواه قرمز کن ، اون یکی مولفه هم آبی کن ! یعنی با ۲ تا رنگ هم میشه یه کاری کرد که رو به رو قطری تک رنگ نداشته باشیم .
پاسخ : یک کره و سه رنگ
خب دیگه, ولی شرط سوال میرسونه که اون سه تا مجموعه بسته هستن, چرا؟ فرض کن
همه اونایی باشه که قرمزن, و دنباله
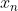به
میل کنه و
قرمز نباشه. در این صورت چون یه دنباله داره به
میل می کنه,
توی
هست, ولی چون
قرمز نیست, پس تو
و در نتیجه تو
هم نیست, پس توی مرز
هست, پس رنگش قرمزه!!! تناقض, پس
بسته است.
علیرضا: تو امتحان ما هم اومده بود!!!!: AoPS Forum - equivalent statements of the borsuk-ulam theorem • Art of Problem Solving
خب دیگه, ولی شرط سوال میرسونه که اون سه تا مجموعه بسته هستن, چرا؟ فرض کن
علیرضا: تو امتحان ما هم اومده بود!!!!: AoPS Forum - equivalent statements of the borsuk-ulam theorem • Art of Problem Solving
پاسخ : یک کره و سه رنگ
دوستان !
من یک راه حل آسون تر برای این سوال پیدا کردم ! :161:
(فقط امیدوارم جوب نداشته باشه چون راه حل های آسون سوالای ترکیبیات معمولا جوب میخورن ! :4
فرض کنید سه تا رنگ اشتراک داشته باشند یعنی هر سه رنگ دو به دو با هم مرز داشته باشند. در اون صورت مرز آبی و قرمز و مرز ابی و سبز و مرز قرمز و سبز تو یک نقطه به هم برخورد کنند . از اونجا که نقاط روی مرز شامل رنگ دو ناحیه هستند پس نقطه ی اشتراک سه تا رنگ هر سه تا رنگ رو داره. حالا اگه از اون نقطه به مرکز کره وصل کنیم و ادامه بدیم تا کره رو قطع کنه این قطر ، قطر مورد نظر ماست!
اگه سه تا رنگ همزمان اشتراک نداشته باشند،تعریف میکنم : رنگ وسط به رنگی میگم که با هر دو تا رنگ دیگه اشتراک داره (چنین رنگی حتما وجود داره و یکتاست _چرا؟_). در این صورت اگه رنگی وجود داشته باشه که بیشتر از مساحت یک نیم کره رو شامل باشه مساله حله. اگه هم چنین نباشه حتما صفحه ای وجود داره که از مرکز کره بگذره و فقط با رنگ وسط برخورد کنه. پس باز هم قطر مورد نظر وجود داره !! :53::172:
دوستان !
من یک راه حل آسون تر برای این سوال پیدا کردم ! :161:
(فقط امیدوارم جوب نداشته باشه چون راه حل های آسون سوالای ترکیبیات معمولا جوب میخورن ! :4
فرض کنید سه تا رنگ اشتراک داشته باشند یعنی هر سه رنگ دو به دو با هم مرز داشته باشند. در اون صورت مرز آبی و قرمز و مرز ابی و سبز و مرز قرمز و سبز تو یک نقطه به هم برخورد کنند . از اونجا که نقاط روی مرز شامل رنگ دو ناحیه هستند پس نقطه ی اشتراک سه تا رنگ هر سه تا رنگ رو داره. حالا اگه از اون نقطه به مرکز کره وصل کنیم و ادامه بدیم تا کره رو قطع کنه این قطر ، قطر مورد نظر ماست!
اگه سه تا رنگ همزمان اشتراک نداشته باشند،تعریف میکنم : رنگ وسط به رنگی میگم که با هر دو تا رنگ دیگه اشتراک داره (چنین رنگی حتما وجود داره و یکتاست _چرا؟_). در این صورت اگه رنگی وجود داشته باشه که بیشتر از مساحت یک نیم کره رو شامل باشه مساله حله. اگه هم چنین نباشه حتما صفحه ای وجود داره که از مرکز کره بگذره و فقط با رنگ وسط برخورد کنه. پس باز هم قطر مورد نظر وجود داره !! :53::172:
آخرین ویرایش توسط مدیر
پاسخ : یک کره و سه رنگ
تیکه دومش فک کنم جوب داره چون مثلن اگه کره رو با n تا صفحه موازی قطع کنیم اینا رو کره n+1 قسمت به وجود میارن که میشه اولی رو قرمز دومی رو سبز سومی رو آبی چهارمی رو قرمز و ... کنیم............:3:
دوستان !
من یک راه حل آسون تر برای این سوال پیدا کردم ! :161:
(فقط امیدوارم جوب نداشته باشه چون راه حل های آسون سوالای ترکیبیات معمولا جوب میخورن ! :4
فرض کنید سه تا رنگ اشتراک داشته باشند یعنی هر سه رنگ دو به دو با هم مرز داشته باشند. در اون صورت مرز آبی و قرمز و مرز ابی و سبز و مرز قرمز و سبز تو یک نقطه به هم برخورد کنند . از اونجا که نقاط روی مرز شامل رنگ دو ناحیه هستند پس نقطه ی اشتراک سه تا رنگ هر سه تا رنگ رو داره. حالا اگه از اون نقطه به مرکز کره وصل کنیم و ادامه بدیم تا کره رو قطع کنه این قطر ، قطر مورد نظر ماست!
اگه سه تا رنگ مرز نداشته باشند،تعریف میکنم : رنگ وسط به رنگی میگم که با هر دو تا رنگ دیگه اشتراک داره (چنین رنگی حتما وجود داره و یکتاست _چرا؟_). در این صورت اگه رنگی وجود داشته باشه که بیشتر از مساحت یک نیم کره رو شامل باشه مساله حله. اگه هم چنین نباشه حتما صفحه ای وجود داره که از مرکز کره بگذره و فقط با رنگ وسط برخورد کنه. پس باز هم قطر مورد نظر وجود داره !! :53::172:
من یک راه حل آسون تر برای این سوال پیدا کردم ! :161:
(فقط امیدوارم جوب نداشته باشه چون راه حل های آسون سوالای ترکیبیات معمولا جوب میخورن ! :4
فرض کنید سه تا رنگ اشتراک داشته باشند یعنی هر سه رنگ دو به دو با هم مرز داشته باشند. در اون صورت مرز آبی و قرمز و مرز ابی و سبز و مرز قرمز و سبز تو یک نقطه به هم برخورد کنند . از اونجا که نقاط روی مرز شامل رنگ دو ناحیه هستند پس نقطه ی اشتراک سه تا رنگ هر سه تا رنگ رو داره. حالا اگه از اون نقطه به مرکز کره وصل کنیم و ادامه بدیم تا کره رو قطع کنه این قطر ، قطر مورد نظر ماست!
اگه سه تا رنگ مرز نداشته باشند،تعریف میکنم : رنگ وسط به رنگی میگم که با هر دو تا رنگ دیگه اشتراک داره (چنین رنگی حتما وجود داره و یکتاست _چرا؟_). در این صورت اگه رنگی وجود داشته باشه که بیشتر از مساحت یک نیم کره رو شامل باشه مساله حله. اگه هم چنین نباشه حتما صفحه ای وجود داره که از مرکز کره بگذره و فقط با رنگ وسط برخورد کنه. پس باز هم قطر مورد نظر وجود داره !! :53::172:
پاسخ : یک کره و سه رنگ
کره سه بخش بیشتر نیست ! :77:
فرض کنیم قرمز رنگ وسط باشه و آبی و سبز هر کدومشون فقط با قرمز مرز داشته باشند. اجازه بدین فرض کنیم آبی و سبز هر دو از یک نیم کره کمترند (چون در اون صورت حتما قطری وجود داره که از دو سرش تو آبی یا سبز باشند).
قطری از دایره رو در نظر بگیرید که یکی از سر هاش تو آبیه و دیگری توی سبز. این قطر رو طوری شروع میکنیم به چرخوندن. تا جایی که یکی از سرهاش بیفته تو ناحیه ی قرمز( دقت داشته باشین که قطر رو طوری میچرخونم که مکان هندسی دو سر این قطر روی کره تشکیل یک دایره میدن. ضمنا رو محیط دایره از هر سه رنگ وجود داره). حالا فرض کنین دو سر این قطر یکیش تو قرمزه و یکیش همون طوری تو ناحیه ی آبی باقی مونده. همچنان به چرخوندن این قطر ادامه میدم. اگر اون یکی سرش هم از آبی بیفته تو قرمز مساله حله . چون این قطر هر دو سرش قرمز شده اند.
حالا ادعا میکنم این اتفاق حتما میفته یعنی هر دو سر این قطر همزمان میفتن تو قرمز. به برهان خلف فرض کنید این اتفاق نیفته. یعنی اون سری که تو قرمز هست یا باید بره تو آبی که در اون صورت ناحیه ی آبی باید بیشتر از نصف نیم کره رو شامل باشه که با فرض ما در تناقضه. یا اون آبیه باید بره تو سبز (بدون این که از قرمز رد بشه) که این هم باز تناقضه چون فرض کردیم آبی و سبز اشتراکی ندارند !! و تمام ! :88:
کره سه بخش بیشتر نیست ! :77:
فرض کنیم قرمز رنگ وسط باشه و آبی و سبز هر کدومشون فقط با قرمز مرز داشته باشند. اجازه بدین فرض کنیم آبی و سبز هر دو از یک نیم کره کمترند (چون در اون صورت حتما قطری وجود داره که از دو سرش تو آبی یا سبز باشند).
قطری از دایره رو در نظر بگیرید که یکی از سر هاش تو آبیه و دیگری توی سبز. این قطر رو طوری شروع میکنیم به چرخوندن. تا جایی که یکی از سرهاش بیفته تو ناحیه ی قرمز( دقت داشته باشین که قطر رو طوری میچرخونم که مکان هندسی دو سر این قطر روی کره تشکیل یک دایره میدن. ضمنا رو محیط دایره از هر سه رنگ وجود داره). حالا فرض کنین دو سر این قطر یکیش تو قرمزه و یکیش همون طوری تو ناحیه ی آبی باقی مونده. همچنان به چرخوندن این قطر ادامه میدم. اگر اون یکی سرش هم از آبی بیفته تو قرمز مساله حله . چون این قطر هر دو سرش قرمز شده اند.
حالا ادعا میکنم این اتفاق حتما میفته یعنی هر دو سر این قطر همزمان میفتن تو قرمز. به برهان خلف فرض کنید این اتفاق نیفته. یعنی اون سری که تو قرمز هست یا باید بره تو آبی که در اون صورت ناحیه ی آبی باید بیشتر از نصف نیم کره رو شامل باشه که با فرض ما در تناقضه. یا اون آبیه باید بره تو سبز (بدون این که از قرمز رد بشه) که این هم باز تناقضه چون فرض کردیم آبی و سبز اشتراکی ندارند !! و تمام ! :88:
پاسخ : یک کره و سه رنگ
اگه تو صورت سوال گفته باشه که اون سه تا بخش همبندن میشه با راه های آسون تر هم حلش کرد, ولی اگه نباشه, تنها چیزی که ما در موردشون میدونیم اینه که بسته هستن (یعنی اگه یه سری از نقاط یه رنگ (مثلا قرمز) به نقطه ای میل کنن, اونوقت اون نقطه هم قرمزه) و مجموعه های بسته روی کره میتونن شکل های خیلی وحشتناکی داشته باشن. :3:
گرچه منم حدسم اینه که منظور سوال این بوده که اون سه تا بخش همبند باشن, چون اگه نباشن دادن این سوال تو یه امتحان المپیادی واقعا نامردیه!!! :4:
اگه تو صورت سوال گفته باشه که اون سه تا بخش همبندن میشه با راه های آسون تر هم حلش کرد, ولی اگه نباشه, تنها چیزی که ما در موردشون میدونیم اینه که بسته هستن (یعنی اگه یه سری از نقاط یه رنگ (مثلا قرمز) به نقطه ای میل کنن, اونوقت اون نقطه هم قرمزه) و مجموعه های بسته روی کره میتونن شکل های خیلی وحشتناکی داشته باشن. :3:
گرچه منم حدسم اینه که منظور سوال این بوده که اون سه تا بخش همبند باشن, چون اگه نباشن دادن این سوال تو یه امتحان المپیادی واقعا نامردیه!!! :4: