دو سوال از همگرایی دنباله ها
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : دو سوال دارم هر کدوم حل کردی یعنی کارت درسته!!!
a(n) /a(n+1) Lim n->infinity
رو حساب میکنیم.اگر به صفر میل کنه همگراست.
یک کار دیگه که به فکرم میرسه تغغیر متغیره.1/n رو بگیریم u و u رو به صفر میل بدیم.که این جوری بنظر میرسه به ازای n بینهایت جواب باید بشه صفر !یعنی به صفر میل میکنه چون میشه usin(1/u) و sin بین -1 تا 1 هست و داره تو ی یک چیز کوچیک ضرب میشه.پس باید به صفر میل کنه.
a(n) /a(n+1) Lim n->infinity
رو حساب میکنیم.اگر به صفر میل کنه همگراست.
یک کار دیگه که به فکرم میرسه تغغیر متغیره.1/n رو بگیریم u و u رو به صفر میل بدیم.که این جوری بنظر میرسه به ازای n بینهایت جواب باید بشه صفر !یعنی به صفر میل میکنه چون میشه usin(1/u) و sin بین -1 تا 1 هست و داره تو ی یک چیز کوچیک ضرب میشه.پس باید به صفر میل کنه.
- ارسال ها
- 107
- لایک ها
- 53
- امتیاز
- 0
پاسخ : دو سوال دارم هر کدوم حل کردی یعنی کارت درسته!!!
من سوال دوم رو تا یه جایی رفتم ولی بقیشو گیر کردم:
تابع زیر را اینگونه تعریف می کنیم:
=\sum_{n=0}^{\infty&space;}\frac{(-1)^{n}}{(2n+1)!}x^{2n+2}=x.\sin&space;x)
حالا اگر از تابع مشتق بگیریم داریم:
=\sum_{n=0}^{\infty&space;}\frac{(-1)^{n}(2n+2)}{(2n+1)!}x^{2n+1})
حالا اگر ثابت کنیم که
>&space;0))
می تونیم بگیم که این دنباله همگراست!
که اینجاشو موندم چطوری ثابت کنم. البته مطمئن نیستم تا اینجاشم درست است یا نه!
من سوال دوم رو تا یه جایی رفتم ولی بقیشو گیر کردم:
تابع زیر را اینگونه تعریف می کنیم:
حالا اگر ثابت کنیم که
که اینجاشو موندم چطوری ثابت کنم. البته مطمئن نیستم تا اینجاشم درست است یا نه!
- ارسال ها
- 107
- لایک ها
- 53
- امتیاز
- 0
پاسخ : دو سوال دارم هر کدوم حل کردی یعنی کارت درسته!!!
در ادامه داریم:
=x.\cos&space;x&space;+&space;\sin&space;x)
چون مقدار این تابع به ازای مقادیر مختلف هم میتونه مثبت هم صفر و هم منفی باشه پس دنباله ی
همگرا نیست.
البته تو پست قبلیمم گفتم که مطمئن نیستم راهم درست باشه یا نه!:225::106:
اینم بگم اون بسط تیلور و مشتقش کار اضافه بود. اصلا حواسم به اصل تابع نبود. :35::35::35:
من سوال دوم رو تا یه جایی رفتم ولی بقیشو گیر کردم:
تابع زیر را اینگونه تعریف می کنیم:
حالا اگر از تابع مشتق بگیریم داریم:
حالا اگر ثابت کنیم که
می تونیم بگیم که این دنباله همگراست!
که اینجاشو موندم چطوری ثابت کنم. البته مطمئن نیستم تا اینجاشم درست است یا نه!
تابع زیر را اینگونه تعریف می کنیم:
حالا اگر ثابت کنیم که
که اینجاشو موندم چطوری ثابت کنم. البته مطمئن نیستم تا اینجاشم درست است یا نه!
چون مقدار این تابع به ازای مقادیر مختلف هم میتونه مثبت هم صفر و هم منفی باشه پس دنباله ی
البته تو پست قبلیمم گفتم که مطمئن نیستم راهم درست باشه یا نه!:225::106:
اینم بگم اون بسط تیلور و مشتقش کار اضافه بود. اصلا حواسم به اصل تابع نبود. :35::35::35:
آخرین ویرایش توسط مدیر
پاسخ : دو سوال دارم هر کدوم حل کردی یعنی کارت درسته!!!
من سال پیش که سوال اول رو حل کردم راه قشنگ و راحتی بود برای همین چند گام اول راه حلمو میزارم تا خودتون حلش کنید.
در ضمن از تمامی کاربرا خصوصا threehandsnal ,pooriya,goodarz, و...... تشکر میکنم.
ابتدا قضیه زیر را بیان میکنیم(اثبات به عهده خودتون): در قسمت اعشاری هر عدد گنگی یک رقم هستش که تا آخر وجود دارد (یعنی تکرار میشه)(اگر منظورمو متوجه نشدین بگین).
فرض میکنیم ان رقم K باشد و در جایگاهای x_2,x_1, ... باشد بعد به صورت زیر عمل میکنیم:
و اگر همین کار را ادامه دهیم میبینیم تا بینهایت ما حاصل
خواهیم داشت پس اگر f میخواهد همگرا باشد باید یا به
و یا به
همگرا باشد حالا شما ثابت کنید که به هیچ کدوم نمی تواند همگرا باشد 
در ضمن اگر به قضیه زیر احتیاج پیدا کردین استفاده کنین:
در قسمت اعشاری هر عدد گنگی حتما دو رقم
وجود دارند که تا آخر تکرار شوند.
من سال پیش که سوال اول رو حل کردم راه قشنگ و راحتی بود برای همین چند گام اول راه حلمو میزارم تا خودتون حلش کنید.
در ضمن از تمامی کاربرا خصوصا threehandsnal ,pooriya,goodarz, و...... تشکر میکنم.
ابتدا قضیه زیر را بیان میکنیم(اثبات به عهده خودتون): در قسمت اعشاری هر عدد گنگی یک رقم هستش که تا آخر وجود دارد (یعنی تکرار میشه)(اگر منظورمو متوجه نشدین بگین).
فرض میکنیم ان رقم K باشد و در جایگاهای x_2,x_1, ... باشد بعد به صورت زیر عمل میکنیم:
در ضمن اگر به قضیه زیر احتیاج پیدا کردین استفاده کنین:
در قسمت اعشاری هر عدد گنگی حتما دو رقم
پاسخ : دو سوال دارم هر کدوم حل کردی یعنی کارت درسته!!!
اشباه کردی دوستم!اولا این یک دنباله است یعنی اگر مقادیر ان مثبت و منفی شود دلیلی بر واگرایی آن نیست مثلا
که تا بینهایت مثبت منفی میشه یا اگر هم تابع باشه مثال نقض داریم مثل
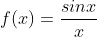
ولی ممنون از ایده ی جالبت
در ادامه داریم:
چون مقدار این تابع به ازای مقادیر مختلف هم میتونه مثبت هم صفر و هم منفی باشه پس دنباله ی
همگرا نیست.
البته تو پست قبلیمم گفتم که مطمئن نیستم راهم درست باشه یا نه!:225::106:
اینم بگم اون بسط تیلور و مشتقش کار اضافه بود. اصلا حواسم به اصل تابع نبود. :35::35::35:
چون مقدار این تابع به ازای مقادیر مختلف هم میتونه مثبت هم صفر و هم منفی باشه پس دنباله ی
البته تو پست قبلیمم گفتم که مطمئن نیستم راهم درست باشه یا نه!:225::106:
اینم بگم اون بسط تیلور و مشتقش کار اضافه بود. اصلا حواسم به اصل تابع نبود. :35::35::35:
که تا بینهایت مثبت منفی میشه یا اگر هم تابع باشه مثال نقض داریم مثل
ولی ممنون از ایده ی جالبت
پاسخ : دو سوال دارم هر کدوم حل کردی یعنی کارت درسته!!!
اشتباه تایپی: اونجا که گفتم پس اگر دنباله میخواهد همگرا باشد باید یا به
و یا به
اشتباه است.در حقیقت ثابت شده که اگه همگرا باشه به عددی بین
و
همگرا است.
راستی برای اثبات مسئله از قضیه 2 که گفتم استتفاده کنید الان برای شما قضیه 2 رو اثبات میکنم و قضیه 1 هم مثل اون اثبات میشه::
اثبات :فرض میکنیم هیچ دو عددی به صورت
تا آخر ادامه نیابد یعنی از جایی به بعد وجود نداشته باشد حالا چون ما 10 رقم داریم تعداد اعداد دو رقمی محدوده پس عدد ما مختومه که با فرض گنگ بودنس تناقص داره
من سال پیش که سوال اول رو حل کردم راه قشنگ و راحتی بود برای همین چند گام اول راه حلمو میزارم تا خودتون حلش کنید.
در ضمن از تمامی کاربرا خصوصا threehandsnal ,pooriya,goodarz, و...... تشکر میکنم.
1) ابتدا قضیه زیر را بیان میکنیم(اثبات به عهده خودتون): در قسمت اعشاری هر عدد گنگی یک رقم هستش که تا آخر وجود دارد (یعنی تکرار میشه)(اگر منظورمو متوجه نشدین بگین).
فرض میکنیم ان رقم K باشد و در جایگاهای x_2,x_1, ...باشد بعد به صورت زیر عمل میکنیم:
و اگر همین کار را ادامه دهیم میبینیم تا بینهایت ما حاصل
خواهیم داشت پس اگر f میخواهد همگرا باشد باید یا به
و یا به
همگرا باشد حالا شما ثابت کنید که به هیچ کدوم نمی تواند همگرا باشد
در ضمن اگر به قضیه زیر احتیاج پیدا کردین استفاده کنین:
2) در قسمت اعشاری هر عدد گنگی حتما دو رقم
وجود دارند که تا آخر تکرار شوند.
در ضمن از تمامی کاربرا خصوصا threehandsnal ,pooriya,goodarz, و...... تشکر میکنم.
1) ابتدا قضیه زیر را بیان میکنیم(اثبات به عهده خودتون): در قسمت اعشاری هر عدد گنگی یک رقم هستش که تا آخر وجود دارد (یعنی تکرار میشه)(اگر منظورمو متوجه نشدین بگین).
فرض میکنیم ان رقم K باشد و در جایگاهای x_2,x_1, ...باشد بعد به صورت زیر عمل میکنیم:
در ضمن اگر به قضیه زیر احتیاج پیدا کردین استفاده کنین:
2) در قسمت اعشاری هر عدد گنگی حتما دو رقم
اشتباه تایپی: اونجا که گفتم پس اگر دنباله میخواهد همگرا باشد باید یا به
راستی برای اثبات مسئله از قضیه 2 که گفتم استتفاده کنید الان برای شما قضیه 2 رو اثبات میکنم و قضیه 1 هم مثل اون اثبات میشه::
اثبات :فرض میکنیم هیچ دو عددی به صورت
