معرفی تایع ( پیوستگی و مشتق پذیری)
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : معرفی تایع ( پیوستگی و مشتق پذیری)
ضد شهود ترین تابع ممکن در این زمینه:
تابع وایراشتراوس...همه جا پیوسته...هیچ جا مشتق پزیر نیست ولی!!
Weierstrass function - Wikipedia, the free encyclopedia
و سوالت رو خوب نمیفهمم...یعنی تو n نقطه مشتقپذیر باشه..تو m نقطه پیوسته باشه و مشتق ناپذیر؟؟
و تابع رو با هرچند تا ضابطه میتونیم تعریف کنیم!؟
ضد شهود ترین تابع ممکن در این زمینه:
تابع وایراشتراوس...همه جا پیوسته...هیچ جا مشتق پزیر نیست ولی!!
Weierstrass function - Wikipedia, the free encyclopedia
و سوالت رو خوب نمیفهمم...یعنی تو n نقطه مشتقپذیر باشه..تو m نقطه پیوسته باشه و مشتق ناپذیر؟؟
و تابع رو با هرچند تا ضابطه میتونیم تعریف کنیم!؟
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : معرفی تایع ( پیوستگی و مشتق پذیری)
جوابتو بزار ببینیم دیگه.
باید یک ضابطه ای باشه؟؟اگه نه که کاری نداره..ولی اگه آره..باز هم راه های مختلفی داره...
فعلن جوابتو بزار ببنیم.
کلن هر تابعی رو میشه بشکل ضرایب خطی هر دسته توابع ارتونورمال نوشت.
مثل سینوس و کسینوی..لژاندر..هرمیت..لاگر..چبی شف..بسل و...
یعنی عملن از یک سری از اینها(سینوس ها و کسینوسها..لژاندر ها و لژاندر ها..لاگرا و لاگرا...)میشه مجانبی(هر چقدر خاستیم به هر تابعی..حتی بدقلق نزدیک شیم)
فقط سری سینوس کسینوس ها یک مشکل داره..
اثر گیبز.(من گیبز رو خیلی دوسش دارم!)
http://en.wikipedia.org/wiki/Gibbs_phenomenon
یک شرایط هم هست...
http://en.wikipedia.org/wiki/Dirichlet_conditions
که الان من نمیدونم منظور طراح سوال اصلن اینا بوده یا نه..
فکر نکنم منظورش دیریکله و فوریه بازی بوده.
جوابتو بزار ببینیم دیگه.
باید یک ضابطه ای باشه؟؟اگه نه که کاری نداره..ولی اگه آره..باز هم راه های مختلفی داره...
فعلن جوابتو بزار ببنیم.
کلن هر تابعی رو میشه بشکل ضرایب خطی هر دسته توابع ارتونورمال نوشت.
مثل سینوس و کسینوی..لژاندر..هرمیت..لاگر..چبی شف..بسل و...
یعنی عملن از یک سری از اینها(سینوس ها و کسینوسها..لژاندر ها و لژاندر ها..لاگرا و لاگرا...)میشه مجانبی(هر چقدر خاستیم به هر تابعی..حتی بدقلق نزدیک شیم)
فقط سری سینوس کسینوس ها یک مشکل داره..
اثر گیبز.(من گیبز رو خیلی دوسش دارم!)
http://en.wikipedia.org/wiki/Gibbs_phenomenon
یک شرایط هم هست...
http://en.wikipedia.org/wiki/Dirichlet_conditions
که الان من نمیدونم منظور طراح سوال اصلن اینا بوده یا نه..
فکر نکنم منظورش دیریکله و فوریه بازی بوده.
آخرین ویرایش توسط مدیر
پاسخ : معرفی تایع ( پیوستگی و مشتق پذیری)
g رو یک چندجمله ای در نظر بگیرید با این شرایط:
1) دقیقا m ریشه داشته باشد که مشتقش در آن نقاط صفر نیست.
2) دقیقا n ریشه داشته باشد که مشتقش در آن نقاط صفر است.
مثلا اگر x_i ها و y_i ها حقیقی و متمایز باشند، چندجمله ای روبرو دارای این شرایط است:
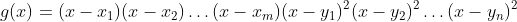
حالا تابع f رو به صورت زیر تعریف می کنیم:
که شرایط مسئله رو داره.
g رو یک چندجمله ای در نظر بگیرید با این شرایط:
1) دقیقا m ریشه داشته باشد که مشتقش در آن نقاط صفر نیست.
2) دقیقا n ریشه داشته باشد که مشتقش در آن نقاط صفر است.
مثلا اگر x_i ها و y_i ها حقیقی و متمایز باشند، چندجمله ای روبرو دارای این شرایط است:
حالا تابع f رو به صورت زیر تعریف می کنیم:
که شرایط مسئله رو داره.
پاسخ : معرفی تایع ( پیوستگی و مشتق پذیری)
اول تابع f رو به صورت زیر تعریف می کنیم.
حالا تابع g رو با دامنه محدود و دیریکته ای تعریف می کنم.
=\begin{cases} sinx & \text{ if } x=Q \\ cosx & \text{ if } x=Q' \end{cases})
این واسه شرط اولیه بود.نمودارشون رو رسم کنید منظورم رو می فهمید.
حالا واسه شرط دوم داریم.
)
=\begin{cases} sinx & \text{ if } x=Q \\ -sinx+2 & \text{ if } x=Q' \end{cases})
ویرایش:البته توی تابع h چون توی غربی ترین بخش تابع مشتق چپ نداریم مثلا 0.1 دامنه رو بیارید غرب تر!!!
اول تابع f رو به صورت زیر تعریف می کنیم.
حالا تابع g رو با دامنه محدود و دیریکته ای تعریف می کنم.
این واسه شرط اولیه بود.نمودارشون رو رسم کنید منظورم رو می فهمید.
حالا واسه شرط دوم داریم.
ویرایش:البته توی تابع h چون توی غربی ترین بخش تابع مشتق چپ نداریم مثلا 0.1 دامنه رو بیارید غرب تر!!!
آخرین ویرایش توسط مدیر
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : معرفی تایع ( پیوستگی و مشتق پذیری)
مشکل سوال همینه!!!
اصلن نگفته چی میخواد!!یک تابع چندضابطه ای میخواد؟یک تابع چندجمله ای میخواد؟
خیلی جوریا میشه گفت چنین تابعی...دامنه اش رو دستی محدود کنیم یا نه؟و...
حالا یک سوال کسی میتونه وایراشتراوس رو ثابت کنه؟
اول تابع f رو به صورت زیر تعریف می کنیم.
حالا تابع g رو با دامنه محدود و دیریکته ای تعریف می کنم.
=\begin{cases}%20sinx%20&%20\text{%20if%20}%20x=Q%20\\%20cosx%20&%20\text{%20if%20}%20x=Q'%20\end{cases})
این واسه شرط اولیه بود.نمودارشون رو رسم کنید منظورم رو می فهمید.
حالا واسه شرط دوم داریم.
)
=\begin{cases}%20sinx%20&%20\text{%20if%20}%20x=Q%20\\%20-sinx+2%20&%20\text{%20if%20}%20x=Q'%20\end{cases})
حالا تابع g رو با دامنه محدود و دیریکته ای تعریف می کنم.
این واسه شرط اولیه بود.نمودارشون رو رسم کنید منظورم رو می فهمید.
حالا واسه شرط دوم داریم.
اصلن نگفته چی میخواد!!یک تابع چندضابطه ای میخواد؟یک تابع چندجمله ای میخواد؟
خیلی جوریا میشه گفت چنین تابعی...دامنه اش رو دستی محدود کنیم یا نه؟و...
حالا یک سوال کسی میتونه وایراشتراوس رو ثابت کنه؟
پاسخ : معرفی تایع ( پیوستگی و مشتق پذیری)
تابع خودم هم شبیه همین بود فقط به ازای x های گنگ به جای
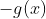, 0 گذاشتم .( تمیز تره نه!!):98:
g رو یک چندجمله ای در نظر بگیرید با این شرایط:
1) دقیقا m ریشه داشته باشد که مشتقش در آن نقاط صفر نیست.
2) دقیقا n ریشه داشته باشد که مشتقش در آن نقاط صفر است.
مثلا اگر x_i ها و y_i ها حقیقی و متمایز باشند، چندجمله ای روبرو دارای این شرایط است:
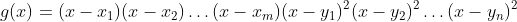
حالا تابع f رو به صورت زیر تعریف می کنیم:
که شرایط مسئله رو داره.
1) دقیقا m ریشه داشته باشد که مشتقش در آن نقاط صفر نیست.
2) دقیقا n ریشه داشته باشد که مشتقش در آن نقاط صفر است.
مثلا اگر x_i ها و y_i ها حقیقی و متمایز باشند، چندجمله ای روبرو دارای این شرایط است:
حالا تابع f رو به صورت زیر تعریف می کنیم:
که شرایط مسئله رو داره.
