پاسخ : ترکیب
یک اشتباه کوچیک! صفر رو حساب نکردم !
لطفا راه حلتون رو هم بگيد ، چون جوابتون صحيح نيست.
راهنمايي: سوال تعداد سه تايي هاي
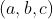رو مي خواد كه
. حالا از تغيير متغير زير ببينيد چه استفاده اي ميشه كرد...
راهنمايي: سوال تعداد سه تايي هاي
1+3+6+10+15+21+28+36=120
اگه درسته بگید که راه حل رو بگم اگه نه یک فرصت دیگه!!
اگه درسته بگید که راه حل رو بگم اگه نه یک فرصت دیگه!!
آخرین ویرایش توسط مدیر
پاسخ : ترکیب
راه حل ! :
بررسی حالات مختلف :
کوچکترین رقم ممکن برای صدگان 2 است .... -> دهگان 1 و یکان 0
حالت بعد : اگر صد گان 3باشد دو حالت برای دهگان میماند 1 و 2 اگر 1باشد تنها حالت برای یکان 0 است. اگر هم 2 باشد یکان می تواند 1 و 0 باشد.
همین حالت را ادامه دهیم به این توالی میرسیم
1
3
6
10
.
.
.
36
به هرجمله x اضافه می شود و به خود x هربار یکی اضافه میشود!
راه حل ! :
بررسی حالات مختلف :
کوچکترین رقم ممکن برای صدگان 2 است .... -> دهگان 1 و یکان 0
حالت بعد : اگر صد گان 3باشد دو حالت برای دهگان میماند 1 و 2 اگر 1باشد تنها حالت برای یکان 0 است. اگر هم 2 باشد یکان می تواند 1 و 0 باشد.
همین حالت را ادامه دهیم به این توالی میرسیم
1
3
6
10
.
.
.
36
به هرجمله x اضافه می شود و به خود x هربار یکی اضافه میشود!
پاسخ : ترکیب
این کارم میشه کرد: تعداد زیر مجوعه های 3 عضوی مجموعه ی 10 عضوی شامل 0 تا 9 رو روحساب کرد. چون اگه اعضای هر کدوم از این زیر مجموعه هارو به ترتیب نزولی بنویسیم عدد حاصل یکی از جوابای این مسئلس. درنتیجه یه تناظر یک به یک بین اعداد سه رقمی باشرایط خواسته شده و زیر مجموعه های 3 عضوی یه مجموعه ی 10 عضوی هست. پس جواب هردوشون میشه c(10,3
لطفا شمام بیشتر راجه به راه حلتون توضیح بدین
این کارم میشه کرد: تعداد زیر مجوعه های 3 عضوی مجموعه ی 10 عضوی شامل 0 تا 9 رو روحساب کرد. چون اگه اعضای هر کدوم از این زیر مجموعه هارو به ترتیب نزولی بنویسیم عدد حاصل یکی از جوابای این مسئلس. درنتیجه یه تناظر یک به یک بین اعداد سه رقمی باشرایط خواسته شده و زیر مجموعه های 3 عضوی یه مجموعه ی 10 عضوی هست. پس جواب هردوشون میشه c(10,3
لطفا شمام بیشتر راجه به راه حلتون توضیح بدین
آخرین ویرایش توسط مدیر