تعمیم فوئرباخ
پاسخ : تعمیم فوئرباخ
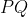را امتداد می دهیم تا دایره ی محیطی
را در
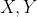قطع کند. خطوط سیمسون
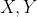را رسم می کنیم تا یکدیگر را در
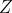قطع کنند.(این خطوط سیمسون برهم عمودند.)
نشان می دهیم
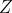محل تماس دایره ی پایی
با دایره ی نه نقطه ی مثلث
است. می دانیم
-مرکز ارتفاعی مثلث
- مرکز تجانس مستقیم دایره ی نه نقطه ی و دایره ی محیطی مثلث
است.
همچنین می دانیم که وسط های
به ترتیب رو خطوط سیمسون
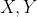قرار دارد. ان ها را
بنامید.
با تجانس به مرکز
و نسبت
نقاط
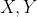به نقاط
تبدیل می شوند. پس
دو سر یک قطر در دایره ی نه نقطه هستند که
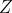آن قطر را با زاویه ی قائمه می بیند. پس
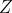روی دایره ی نه نقطه ی مثلث
قرار دارد.
پای عمود نقاط
بر ضلع
را به ترتیب
بنامید. به همین ترتیب
هم تعریف می شوند.
واضح است که داریم:
بنابراین نسبت قوت های سه نقطه ی
نسبت به دایره های پایی
و دایره ی نقطه ی
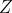ثابت است. پس
روی یک دایره قرار دارند که با دایره ی پایی
و دایره ی نقطه ی
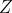هم محور است.
بنابراین نتیجه می شود که دایره ی نه نقطه و دایره ی پایی
در نقطه ی
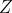بر هم مماسند.
نشان می دهیم
همچنین می دانیم که وسط های
با تجانس به مرکز
پای عمود نقاط
واضح است که داریم:
بنابراین نسبت قوت های سه نقطه ی
بنابراین نتیجه می شود که دایره ی نه نقطه و دایره ی پایی