جدول n در n
پاسخ : جدول n در n
یه سوال فنی !
وقتی میگین سطر رو میشه جایگشت داد ، منظور اینه که فقط این حالتو داریم :
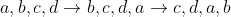(یه چی شبیه جایگشت دوری) یا نه کلاً میتونیم چینش سطر رو به هر طریق که میخوایم عوض کنیم؟ مثلاً :
اگه مورد دوم باشه که فک کنم سوال خیلی راحت باشه !
در هر خانه از یک جدول
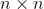یک عدد حقیقی نوشته شده است. می دانیم در هیچ سطری، دو عدد تکراری نداریم.
ثابت کنید می توان اعداد تعدادی سطر را جایگشت داد (درون خود سطر) به طوری که در هیچ ستونی نیز عدد تکراری نباشد.
ثابت کنید می توان اعداد تعدادی سطر را جایگشت داد (درون خود سطر) به طوری که در هیچ ستونی نیز عدد تکراری نباشد.
وقتی میگین سطر رو میشه جایگشت داد ، منظور اینه که فقط این حالتو داریم :
اگه مورد دوم باشه که فک کنم سوال خیلی راحت باشه !
پاسخ : جدول n در n
من دیروز همینطوری حلش کردم، الآن که دیدم میگید راهش خیلی راحت نیست، گفتم راهمو بگم شاید غلط باشه! برای 1 در 1 درسته، فرض میکنیم برای n در n درست باشه، حالا n + 1 در n + 1 رو در نظر بگیرید:
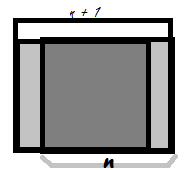
خب حالا اگه برای هر کدوم از این n در n ها ما بیایم درستشون کنیم (طبق فرض استقرا میتونیم) جدول n در n + 1 یی به وجود میاد که شرایط رو داره، حالا میمونه سطر بالا، که اون رو هم میشه جوری جایگشت داد که جدول باز هم درست بشه(چرا؟) ، پس (P(n) => P(n + 1 و ok! حالا اگه غلطه، یا نیاز به توضیح بیشتر دارید، بگید.
من دیروز همینطوری حلش کردم، الآن که دیدم میگید راهش خیلی راحت نیست، گفتم راهمو بگم شاید غلط باشه! برای 1 در 1 درسته، فرض میکنیم برای n در n درست باشه، حالا n + 1 در n + 1 رو در نظر بگیرید:
خب حالا اگه برای هر کدوم از این n در n ها ما بیایم درستشون کنیم (طبق فرض استقرا میتونیم) جدول n در n + 1 یی به وجود میاد که شرایط رو داره، حالا میمونه سطر بالا، که اون رو هم میشه جوری جایگشت داد که جدول باز هم درست بشه(چرا؟) ، پس (P(n) => P(n + 1 و ok! حالا اگه غلطه، یا نیاز به توضیح بیشتر دارید، بگید.
پاسخ : جدول n در n
برا من یه سوال پیش اومد:
اون مربه n*nاول درست!اما وقتی میاید ومربع n*nبغلش رو هم درست میکنید.چون این دو مربعn-1 عدد در هر سطر اشتراک دارن
با درست کردن این شاید اون یکی درست نشه!
اینجاش اثبات داره که میشه انجام داد؟
من دیروز همینطوری حلش کردم، الآن که دیدم میگید راهش خیلی راحت نیست، گفتم راهمو بگم شاید غلط باشه! برای 1 در 1 درسته، فرض میکنیم برای n در n درست باشه، حالا n + 1 در n + 1 رو در نظر بگیرید:
خب حالا اگه برای هر کدوم از این n در n ها ما بیایم درستشون کنیم (طبق فرض استقرا میتونیم) جدول n در n + 1 یی به وجود میاد که شرایط رو داره، حالا میمونه سطر بالا، که اون رو هم میشه جوری جایگشت داد که جدول باز هم درست بشه(چرا؟) ، پس (P(n) => P(n + 1 و ok! حالا اگه غلطه، یا نیاز به توضیح بیشتر دارید، بگید.
خب حالا اگه برای هر کدوم از این n در n ها ما بیایم درستشون کنیم (طبق فرض استقرا میتونیم) جدول n در n + 1 یی به وجود میاد که شرایط رو داره، حالا میمونه سطر بالا، که اون رو هم میشه جوری جایگشت داد که جدول باز هم درست بشه(چرا؟) ، پس (P(n) => P(n + 1 و ok! حالا اگه غلطه، یا نیاز به توضیح بیشتر دارید، بگید.
اون مربه n*nاول درست!اما وقتی میاید ومربع n*nبغلش رو هم درست میکنید.چون این دو مربعn-1 عدد در هر سطر اشتراک دارن
با درست کردن این شاید اون یکی درست نشه!
اینجاش اثبات داره که میشه انجام داد؟
پاسخ : جدول n در n
نکته اش اینجاست که این "چرا" که گفتید درست نمی باشد.
من دیروز همینطوری حلش کردم، الآن که دیدم میگید راهش خیلی راحت نیست، گفتم راهمو بگم شاید غلط باشه! برای 1 در 1 درسته، فرض میکنیم برای n در n درست باشه، حالا n + 1 در n + 1 رو در نظر بگیرید:
خب حالا اگه برای هر کدوم از این n در n ها ما بیایم درستشون کنیم (طبق فرض استقرا میتونیم) جدول n در n + 1 یی به وجود میاد که شرایط رو داره، حالا میمونه سطر بالا، که اون رو هم میشه جوری جایگشت داد که جدول باز هم درست بشه(چرا؟) ، پس (P(n) => P(n + 1 و ok! حالا اگه غلطه، یا نیاز به توضیح بیشتر دارید، بگید.
خب حالا اگه برای هر کدوم از این n در n ها ما بیایم درستشون کنیم (طبق فرض استقرا میتونیم) جدول n در n + 1 یی به وجود میاد که شرایط رو داره، حالا میمونه سطر بالا، که اون رو هم میشه جوری جایگشت داد که جدول باز هم درست بشه(چرا؟) ، پس (P(n) => P(n + 1 و ok! حالا اگه غلطه، یا نیاز به توضیح بیشتر دارید، بگید.
پاسخ : جدول n در n
با دو تا راه میشه این مسعله رو حل کرد
1): با استقرا . حکم به ازای پایه درسته . حالا برای n هم درسته ، میاییم برای n+1 در n+1 میثابتیم!!! مهم همین اثباتش هست،
طبق شکل مثل همون خونه هایی که علامت ضربدر زدم رو مقایسه میکنیم تک تک تا آخر همین طور تا سون های اخر
به عبارتی شکل آخر دورانی 360 درجه برای شکل به وجود میاد :3: این راه 1
---- دو نوشته به هم متصل شده است ----
راه 2 واقعا braining storm
راه 2 رو نمیگم برین تو خماری!!
فقط برای آقای عارف میگم!!!!:204:
با دو تا راه میشه این مسعله رو حل کرد
1): با استقرا . حکم به ازای پایه درسته . حالا برای n هم درسته ، میاییم برای n+1 در n+1 میثابتیم!!! مهم همین اثباتش هست،
طبق شکل مثل همون خونه هایی که علامت ضربدر زدم رو مقایسه میکنیم تک تک تا آخر همین طور تا سون های اخر
به عبارتی شکل آخر دورانی 360 درجه برای شکل به وجود میاد :3: این راه 1
---- دو نوشته به هم متصل شده است ----
راه 2 واقعا braining storm
راه 2 رو نمیگم برین تو خماری!!
فقط برای آقای عارف میگم!!!!:204:
پاسخ : جدول n در n
نمیدونم فک کنم یه چیزی رو نمیفهمم ولی میگم حالا (قول بدید مسخره نکنید :4
با توجه به فرض سوال که توی هر سطر، دو عدد مشابه نداریم ، پس در کل جدول ، تو بد ترین حالت ، n نوع عدد داریم که هر کدوم n بار تکرار شدن و تو هر سطری هم بیش از دوتا عدد مشابه نداریم !
حالا یه عدد مثل i رو که بیشترین بار تکرار شده انتخاب میکنیم ، اگه تو سطر اول بود ، تو یه خونه میذاریمش. میریم سطر بعدی ، بازم در صورت وجود i ، جا گذاریش میکنیم منتهی تو ستونی که قبلاً گذاشتیم ، نمیذاریمش. چون نهایتاً تو بیشترین حالت n تا i داریم ، و n تا ستون ، این کارو تا آخرین سطر میتونیم انجام بدیم.
بعد میریم سراغ عدد بعدی که بعد از i بیشترین بار تکرار شده.
بازم همین کارو میکنیم براش.
بقیه عدد هارو هم همین طوری میتونیم پر کنیم براش و چون حتماً تعداد عددهامون کوچیکتر مساوی nـه ، برای تموم اعداد میتونیم این کارو انجام بدیم.
اشتباهه؟ :217:
نمیدونم فک کنم یه چیزی رو نمیفهمم ولی میگم حالا (قول بدید مسخره نکنید :4
با توجه به فرض سوال که توی هر سطر، دو عدد مشابه نداریم ، پس در کل جدول ، تو بد ترین حالت ، n نوع عدد داریم که هر کدوم n بار تکرار شدن و تو هر سطری هم بیش از دوتا عدد مشابه نداریم !
حالا یه عدد مثل i رو که بیشترین بار تکرار شده انتخاب میکنیم ، اگه تو سطر اول بود ، تو یه خونه میذاریمش. میریم سطر بعدی ، بازم در صورت وجود i ، جا گذاریش میکنیم منتهی تو ستونی که قبلاً گذاشتیم ، نمیذاریمش. چون نهایتاً تو بیشترین حالت n تا i داریم ، و n تا ستون ، این کارو تا آخرین سطر میتونیم انجام بدیم.
بعد میریم سراغ عدد بعدی که بعد از i بیشترین بار تکرار شده.
بازم همین کارو میکنیم براش.
بقیه عدد هارو هم همین طوری میتونیم پر کنیم براش و چون حتماً تعداد عددهامون کوچیکتر مساوی nـه ، برای تموم اعداد میتونیم این کارو انجام بدیم.
اشتباهه؟ :217:
آخرین ویرایش توسط مدیر
پاسخ : جدول n در n
من اینو نگفتم ! (شاید بد گفتم!)
گفتن بدترین حالت زمانیه که تعداد حرفای مشابه بیشتر باشن تو جدول
و هرچی بیشتر باشن ، احتمال اینکه تو یه ستون باشن بیشتره و نیازه که جایگشت بدیم.
حالا اگه کمتر باشن مثلاً از یه حرف دو تا داشته باشیم ، کافیه توی اون دو سطر ، اون حرف مثلاً i رو توی یه ستون قرار ندیم !
ولی اگه مثلاً n تا باشه ، جایگشت دادن سخت تر میشه !
من اینو نگفتم ! (شاید بد گفتم!)
گفتن بدترین حالت زمانیه که تعداد حرفای مشابه بیشتر باشن تو جدول
و هرچی بیشتر باشن ، احتمال اینکه تو یه ستون باشن بیشتره و نیازه که جایگشت بدیم.
حالا اگه کمتر باشن مثلاً از یه حرف دو تا داشته باشیم ، کافیه توی اون دو سطر ، اون حرف مثلاً i رو توی یه ستون قرار ندیم !
ولی اگه مثلاً n تا باشه ، جایگشت دادن سخت تر میشه !
پاسخ : جدول n در n
[/SUP]
مشخص است که تعداد اعداد تکراری بیش از n نیست پس با قرار دادن تمام اعداد در قطر مربع می توان به حکم رسید به همین سادگی :173:
در هر خانه از یک جدول
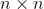یک عدد حقیقی ن[SUP]وشته شده است. می دانیم در هیچ سطری، دو عدد تکراری نداریم.
ثابت کنید می توان اعداد تعدادی سطر را جایگشت داد (درون خود سطر) به طوری که در هیچ ستونی نیز عدد تکراری نباشد.
ثابت کنید می توان اعداد تعدادی سطر را جایگشت داد (درون خود سطر) به طوری که در هیچ ستونی نیز عدد تکراری نباشد.
مشخص است که تعداد اعداد تکراری بیش از n نیست پس با قرار دادن تمام اعداد در قطر مربع می توان به حکم رسید به همین سادگی :173: