جواب های اول معادله
پاسخ : جواب های اول معادله
اول اگه P فرد باشه پس توان 3 زوج میشه و میتونیم طرف چپ رو به صورت اتحاد مزدوج بنویسیم که نتیجه میشه طرف چپ بر 4 بخش پذیره پس r هم باید 2 باشه و 2r[SUP]5[/SUP]=64 و 3 حالت پیش میاد که به راحتی میشه چک کرد که جواب نداره .اگر p زوج باشه برابر 2 و 3[SUP]3p+1[/SUP]=3[SUP]7[/SUP] به پیمانه ی 4 معادله رو بگیریم میشه که r=4k+1 پس min مقدار r برابر 5 . که خیلی ساده هم میشه که q[SUP]2[/SUP] منفی میشه که امکان نداره پس معادله جواب نداره.
چرا سوال نمیدین جواب داشته باشه؟؟؟؟؟
سوال قبلي به اين سوال تغيير پيدا كرد:
چرا سوال نمیدین جواب داشته باشه؟؟؟؟؟
- ارسال ها
- 331
- لایک ها
- 264
- امتیاز
- 0
پاسخ : جواب های اول معادله
ممنون از حل شما...
روش ديگه و مشابه روش شما اينه كه به پيمانه 8 بررسي مي كرديم.
چون اين سوال ها بيشتر طراحي خودمه و بيشتر جنبه آموزشي، بررسي ايده هاي مختلف حل و ... دارند (براي اينه كه بچه هايي كه مي خوان المپياد بدن خوب با ايده ها و روش هاي حل آشنا بشن و در المپياد موفق شوند)
سعي مي كنم سوالاتي هم طرح كنم كه جواب داشته باشه!
موفق و پيروز باشيد.
اول اگه P فرد باشه پس توان 3 زوج میشه و میتونیم طرف چپ رو به صورت اتحاد مزدوج بنویسیم که نتیجه میشه طرف چپ بر 4 بخش پذیره پس r هم باید 2 باشه و 2r[SUP]5[/SUP]=64 و 3 حالت پیش میاد که به راحتی میشه چک کرد که جواب نداره .اگر p زوج باشه برابر 2 و 3[SUP]3p+1[/SUP]=3[SUP]7[/SUP] به پیمانه ی 4 معادله رو بگیریم میشه که r=4k+1 پس min مقدار r برابر 5 . که خیلی ساده هم میشه که q[SUP]2[/SUP] منفی میشه که امکان نداره پس معادله جواب نداره.
چرا سوال نمیدین جواب داشته باشه؟؟؟؟؟
چرا سوال نمیدین جواب داشته باشه؟؟؟؟؟
روش ديگه و مشابه روش شما اينه كه به پيمانه 8 بررسي مي كرديم.
چون اين سوال ها بيشتر طراحي خودمه و بيشتر جنبه آموزشي، بررسي ايده هاي مختلف حل و ... دارند (براي اينه كه بچه هايي كه مي خوان المپياد بدن خوب با ايده ها و روش هاي حل آشنا بشن و در المپياد موفق شوند)
سعي مي كنم سوالاتي هم طرح كنم كه جواب داشته باشه!
موفق و پيروز باشيد.
پاسخ : جواب های اول معادله
ببخشید اگه یکم طولانیه راه حل های من برای سوال های نظریه اعداد همشون اینجوریند.
اول به پیمانه ی p,q در نظر می گیریم:
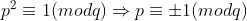
می دونیم که p یکی از دو عبارت بالا رو میشمره اما واضحه که p نمی تونه q+1 رو بشماره(سوال برای q=2 جوابی نداره) پس داریم:
حالا دو حالت رو در نظر می گیریم:
1-
پس به ازای یک k طبیعی خواهیم داشت:
که تناقضه و می دونیم که q+k-1 نمی تونه برابر با صفر باشه. پس این حالت جوابی نداره.
2-
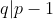
پس به ازای یک k طبیعی خواهیم داشت:
اول فرض کنید q-k-1 بزرگتر از صفر باشه پس داریم:
که تناقضه. حالت بعد هم به همین ترتیب رد میشه.پس باید داشته باشیم q=k+1 که باجایگذاری درصورت سوال جواب
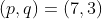بدست میاد.
یه سوال خوب هم من دارم که مال مرحله سه سال 1383 است.
معادله ی
را در مجموعه ی اعداد اول حل کنید.
تمام اعداد اول p,q را بیابید بطوریکه :
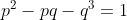
اول به پیمانه ی p,q در نظر می گیریم:
می دونیم که p یکی از دو عبارت بالا رو میشمره اما واضحه که p نمی تونه q+1 رو بشماره(سوال برای q=2 جوابی نداره) پس داریم:
1-
پس به ازای یک k طبیعی خواهیم داشت:
که تناقضه و می دونیم که q+k-1 نمی تونه برابر با صفر باشه. پس این حالت جوابی نداره.
2-
پس به ازای یک k طبیعی خواهیم داشت:
اول فرض کنید q-k-1 بزرگتر از صفر باشه پس داریم:
که تناقضه. حالت بعد هم به همین ترتیب رد میشه.پس باید داشته باشیم q=k+1 که باجایگذاری درصورت سوال جواب
یه سوال خوب هم من دارم که مال مرحله سه سال 1383 است.
معادله ی
- ارسال ها
- 935
- لایک ها
- 1,654
- امتیاز
- 93
پاسخ : جواب های اول معادله
میدونیم :
اگه p بصورت 4k+3 باشه که اونموقع
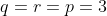
اگه بصورت 4k +1 باشه پس با بررسی دوطرف به پیمانه 4 میفهمیم که
و چون یک مربع کامل به پیمانه 4 برابر با یک یا صفر هستش نتیجه میگیریم که
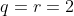که در این صورت جوابی رو در پی نداره
اگه p=2 باشه هم که رد میشه و جواب نداره پس تنها جواب
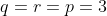
ببخشید اگه یکم طولانیه راه حل های من برای سوال های نظریه اعداد همشون اینجوریند.
اول به پیمانه ی p,q در نظر می گیریم:
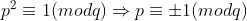
می دونیم که p یکی از دو عبارت بالا رو میشمره اما واضحه که p نمی تونه q+1 رو بشماره(سوال برای q=2 جوابی نداره) پس داریم:
حالا دو حالت رو در نظر می گیریم:
1-
پس به ازای یک k طبیعی خواهیم داشت:
که تناقضه و می دونیم که q+k-1 نمی تونه برابر با صفر باشه. پس این حالت جوابی نداره.
2-
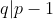
پس به ازای یک k طبیعی خواهیم داشت:
اول فرض کنید q-k-1 بزرگتر از صفر باشه پس داریم:
که تناقضه. حالت بعد هم به همین ترتیب رد میشه.پس باید داشته باشیم q=k+1 که باجایگذاری درصورت سوال جواب
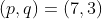بدست میاد.
یه سوال خوب هم من دارم که مال مرحله سه سال 1383 است.
معادله ی
را در مجموعه ی اعداد اول حل کنید.
اول به پیمانه ی p,q در نظر می گیریم:
می دونیم که p یکی از دو عبارت بالا رو میشمره اما واضحه که p نمی تونه q+1 رو بشماره(سوال برای q=2 جوابی نداره) پس داریم:
1-
پس به ازای یک k طبیعی خواهیم داشت:
که تناقضه و می دونیم که q+k-1 نمی تونه برابر با صفر باشه. پس این حالت جوابی نداره.
2-
پس به ازای یک k طبیعی خواهیم داشت:
اول فرض کنید q-k-1 بزرگتر از صفر باشه پس داریم:
که تناقضه. حالت بعد هم به همین ترتیب رد میشه.پس باید داشته باشیم q=k+1 که باجایگذاری درصورت سوال جواب
یه سوال خوب هم من دارم که مال مرحله سه سال 1383 است.
معادله ی
اگه p بصورت 4k+3 باشه که اونموقع
اگه بصورت 4k +1 باشه پس با بررسی دوطرف به پیمانه 4 میفهمیم که
اگه p=2 باشه هم که رد میشه و جواب نداره پس تنها جواب