دور زوج

[navidjalalmanesh]

با استقرا روی n حکم را ثابت می کنیم . پایه استقرا n = 5 است که گراف کامل 5 راسی می شود و حکم درست است.

حکم را برای n-1 درست فرض می کنیم و برای n ثابت می کنیم. اگر در گراف راسی وجود داشته باشد که درجه اش 2 یا کمتر باشد , آن راس را حذف کرده و طبق فرض استقرا دوری زوج داریم (زیرا n-1 راس و حداقل 2n-2 یال داریم) .

در غیر این صورت

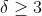است و مسئله تبدیل به ftopicp-44356.html می شود که باز هم دور زوج داریم . پس حکم برای n نیز صحیح است.

 

[mojtabaaa1373]

پاسخ : دور زوج

پس سوالش کو؟؟