لطفا اگر مطلبی مرتبط با این سوال هندسه دیده بودید بگید، البته این سوال فقط حدسه اما sketch اون در تمام حالت ها درست جواب داده:
اگر
 خط دلخواهی باشد که از مرکز دایره ی محیطی(
خط دلخواهی باشد که از مرکز دایره ی محیطی(
 ) مثلث
) مثلث
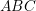 می گذرد و
می گذرد و
 نقطه ای متغیر روی آن باشد، آنگاه با تغییر
نقطه ای متغیر روی آن باشد، آنگاه با تغییر
 دایره ی محیطی مثلث سوایی مزدوج هم زاویه ی
دایره ی محیطی مثلث سوایی مزدوج هم زاویه ی
 ( یعنی
( یعنی
 ) از نقطه ی ثابتی می گذرد. این نقطه ی ثابت همان orthopole خط
) از نقطه ی ثابتی می گذرد. این نقطه ی ثابت همان orthopole خط
 است.
است.
این هم sketch این سوال: http://s1.picofile.com/file/7340887739/Conjecture1.gsp.html
سوال بعدی که به نظر می رسه اثباتش راحت تر از قبلی باشه(البته این هم حدسه):
نقطه ی دلخواه
 در صفحه ی مثلث
در صفحه ی مثلث
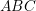 را در نظر بگیرید، مزدوج هم زاویه ی آن نسبت به مثلث
را در نظر بگیرید، مزدوج هم زاویه ی آن نسبت به مثلث
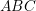 را
را
 می نامیم. ثابت کنید خط واصل
می نامیم. ثابت کنید خط واصل
 و مزدوج هم زاویه اش نسبت به مثلث پایی
و مزدوج هم زاویه اش نسبت به مثلث پایی
 با
با
 موازی است.(
موازی است.(
 مرکز دایره ی محیطی
مرکز دایره ی محیطی
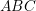 )
)
sketch این سوال: http://s2.picofile.com/file/7340888167/Conjecture2.gsp.html
اگر
این هم sketch این سوال: http://s1.picofile.com/file/7340887739/Conjecture1.gsp.html
سوال بعدی که به نظر می رسه اثباتش راحت تر از قبلی باشه(البته این هم حدسه):
نقطه ی دلخواه
sketch این سوال: http://s2.picofile.com/file/7340888167/Conjecture2.gsp.html
آخرین ویرایش توسط مدیر
