سوال تابع

mimilad · 1390/6/29

همه ی توابع ÷یوسته از اعداد حقیقی به اعداد حقیقی را به گونه ای بیابید که:

$f(x+y)=f(x+f(y))$

گفتم یه سوال بزارم که سایت خالی نباشه .:97:

Aref · 1390/7/1

پاسخ : سوال تابع

امیدوارم جوب نزده باشم.

توابع ثابت همگی جواب مساله هستند. آن ها را کنار می گذاریم.

قرار می دهیم

$x=0$

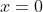و به دست می آوریم

$f(y)=f(f(y))$

.

تعریف می کنیم:

$A=\{x\in \mathbb R | f(x)=x\}$

.

از دو خط بالا نتیجه می گیریم که

$f(\mathbb R)\subseteq A$

.(واضح است که

$A\subseteq f(\mathbb R)$

. پس

$A=f(\mathbb R)$

)

$f$

تابعی غیر ثابت است پس نتیجه می گیریم که

$|A|\ge 2$

دو عضو متمایز از

$A$

مانند

$c,d$

را در نظر میگیریم. فرض کنید

$f(m)=c,f(n)=d,m>n$

. اکنون چون

$f$

تابعی پیوسته است پس طبق قضیه ی مقدار میانی تمامی مقادیر بین

$c,d$

را اختیار میکند.

یعنی داریم

$[c,d]\subseteq A$

. پس به ازای هر مقدار از

$x$

در بازه ی

$[c,d]$

داریم

$f(x)=x$

.

اکنون

$2$

حالت داریم:

-

$f(\mathbb R)$

از بالا یا پایین کراندار نباشد:

در این حالت بدون کاستن از کلیت فرض می کنیم که

$f$

از بالا کراندار نیست. ثابت می کنیم برای هر

$x>d$

داریم

$f(x)=x$

.

$f$

از بالا کراندار نیست پس

$\exists e>x; f(e)=e$

پس طبق قضیه مقدار میانی و مشابه استدلال بالا

$\Rightarrow x\in [d,e]\subseteq A\Rightarrow f(x)=x$

.

حال فرض کنید

$y$

عددی حقیقی و دلخواه باشد. عدد حقیقی

$z$

را طوری انتخاب می کنیم که

$\left\{\begin{matrix} z+y\ge c\\ z+f(y)\ge c \end{matrix}\right.$

داریم

$f(z+y)=f(z+f(y))\Rightarrow z+y=z+f(y)\Rightarrow f(y)=y$

.

-

$f(\mathbb R)$

از بالا و پایین کراندار باشد:

چون

$f$

تابعی پیوسته است پس

$f(\mathbb R)$

سوپریمم و اینفیمم خود را اختیار می کند. فرض کنید

$a=\inf A,b=\sup A$

.

با استفاده از استدلال هایی مشابه بالا نتیجه می گیریم که

$[a,b]\subseteq A$

. که نتیجه می دهد

$[a,b] = A$

.

حال فرض کنید

$y<a$

عددی حقیقی باشد. اگر دستگاه نامعادلات

$\left\{\begin{matrix} a \le x+y \le b\\ a \le x+f(y) \le b \end{matrix}\right.$

جواب داشته باشد، آنگاه (مانند بالا) به وضوح نتیجه می شود که

$f(y)=y$

که تناقض است.

اما دستگاه تنها زمانی جواب ندارد که یکی از دو حالت روبرو پیش بیاید:

$\left\{\begin{matrix} b-a<y-f(y)\\ b-a<f(y)-y \end{matrix}\right.$

.

با میل دادن

$y$

به سمت

$a$

(از پیوستگی

$f$

نتیجه می شود

$f(y)-y$

و نیز

$y-f(y)$

پیوسته هستند.) سمت راست به سمت صفر می رود. اما

$b-a$

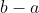مقداری ثابت است. که این تناقض با فرض کراندار بودن

$f$

است.

پس همه ی توابع ثابت و تابع همانی تنها جواب ها هستند. اثبات به پایان می رسد.

threehandsnal · 1390/11/14

پاسخ : سوال تابع

ببخشید منظورتون از این دو خط چی بود؟منظورتون از

$f(\mathbb{R})$

چی بود؟و چرا این دو تا زیرمجموعه همند؟! :

.تعریف می کنیم:

$A=\{x\in \mathbb R | f(x)=x\}$

.

از دو خط بالا نتیجه می گیریم که

$f(\mathbb R)\subseteq A$

.(واضح است که

$A\subseteq f(\mathbb R)$

. پس

$A=f(\mathbb R)$

)

Aref · 1390/11/14

پاسخ : سوال تابع

threehandsnal گفت

$f(\mathbb{R})$

برد f هستش.

$x\in f(\mathbb R)\Rightarrow \exists y\in \mathbb R ,f(y)=x\Rightarrow f(y)=f(f(y))\Rightarrow f(x)=x$

$\Rightarrow x\in A\Rightarrow f(\mathbb R)\subseteq A$

$x\in A \Rightarrow f(x)=x\Rightarrow x=f(x)\in f(\mathbb R)\Rightarrow A\subseteq f(\mathbb R)$

Aref · 1390/11/14

پاسخ : سوال تابع

اثبات هیچ مشکلی نداره.
فقط همون قسمت سوپریمم خود را اختیار میکند یه ذره مشکل داره، که اونم هیچ خللی در روند اثبات ایجاد نمی کنه. چون در اون صورت هم

$A$

برابر یکی از مجموعه های

$\{(a,b),(a,b],[a,b)\}$

می شود.

threehandsnal · 1390/11/14

پاسخ : سوال تابع

اگه تابع پوشا نباشه چی؟اونموقع نمیشه نتیجه گرفت که برد تابع f زیر مجموعه A هست

Aref · 1390/11/14

پاسخ : سوال تابع

threehandsnal گفت

یک عضو از برد -مانند

$x$

- همیشه این خاصیت را دارد که یک عدد حقیقی

$y$

وجود دارد که

$f(y)=x$

.
برد با هم دامنه فرق می کنه.

$\textup{Codomain}\neq \textup{Range}$

threehandsnal · 1390/11/14

پاسخ : سوال تابع

درست میگین.سوتی از من بود.ببخشید

hkh74 · 1390/11/15

پاسخ : سوال تابع

راه حل دوم: واضح است که یکی از جواب های مسئله تابع ثابت است. پس فرض کنیم تابع ثابت نباشد.
فرض مسئله را

$P(x,y)$

در نظر بگیرید:

$P(x,y): f(x+y)=f(x+f(y))$

=======================
ابتدا ثابت می کنیم تابع متناوب جواب مسئله نیست. فرض کنید تابعی با دوره تناوب

$T$

در شرایط مسئله صدق کند. ثابت می کنیم این تابع در بازه ی

$[0,T)$

یک به یک است:
فرض کنید به ازای

$x_0,y_0 \in [0,T) \ ,x_0<y_0$

داشته باشیم

$f(x_0)=f(y_0)$

:

$P(x-x_0,y_0): f(x-x_0+y_0)=f(x-x_0+f(y_0))=f(x-x_0+f(x_0))$

$P(x-x_0,x_0): f(x-x_0+f(x_0))=f(x-x_0+x_0)=f(x)$

$\Rightarrow f(x)=f(x+(y_0-x_0)) \ (\forall x \in \mathbb{R})$

که با توجه به اینکه

$0<y_0-x_0<T$

به تناقض رسیده ایم (زیرا تناوب به دست آمده کوچکتر از تناوب مفروض است)

پس این تابع در بازه ی

$[0,T)$

یک به یک است و در نتیجه (واضح است که) اگر

$f(x)=f(y)$

آنگاه

$\frac{x-y}{T} \in \mathbb{Z}$

:

$P(y,x): f(y+x)=f(y+f(x))\Rightarrow \frac{(y+f(x))-(y+x)}{T} \in \mathbb{Z} \\ \Rightarrow \frac{f(x)-x}{T} \in \mathbb{Z}$

اما

$x \ ,f(x)$

و در نتیجه

$\frac{f(x)-x}{T}$

پیوسته است و

$\frac{f(x)-x}{T} \in \mathbb{Z}$

و واضح است که تنها تابع پیوسته با برد

$\mathbb{Z}$

تابع ثابت است، پس:

$\frac{f(x)-x}{T}=c\Rightarrow f(x)=x+c'$

اما این تابع متناوب نیست، پس به تناقض رسیدیم
=======================

برای حل مسئله ابتدا ثابت می کنیم

$f(x)=0\Leftrightarrow x=0$

:
فرض کنید

$f(x_0)=0 \ ,x_0 \neq 0$

، با توجه به

$P(x,x_0):f(x+x_0)=f(x)$

و اینکه تابع متناوب جواب نیست این حالت رد می شود.
فرض کنید

$f(0)=x_0 \ ,x_0 \neq 0$

، با توجه به

$P(x,0): f(x+x_0)=f(x)$

و اینکه تابع متناوب جواب نیست این حالت نیز رد می شود.

پس ثابت شد

$f(x)=0\Leftrightarrow x=0$

:

$P(-x,x): f(0)=f(-x+f(x))\Leftrightarrow f(f(x)-x)=0\Leftrightarrow f(x)-x=0 \\ \Leftrightarrow f(x)=x$

پس تنها جواب ها توابع ثابت و همانی اند.

threehandsnal · 1390/11/15

پاسخ : سوال تابع

فقط توی این خط یه سوتی کوچولو(توی نوشتن) هستش:

پس این تابع در بازه ی

$[0,T)$

یک به یک است و در نتیجه (واضح است که) اگر

$f(x)=f(y)$

آنگاه

$\frac{f(x)-f(y)}{T} \in \mathbb{Z}$

:

که باید آخرشو اینجوری نوشت:

$f(x)=f(y) \Rightarrow \frac{x-y}{T}\in \mathbb{Z}$

hkh74 · 1390/11/15

پاسخ : سوال تابع

threehandsnal گفت

ممنون. اصلاح شد.

سوال تابع

mimilad

New Member

Aref

New Member

threehandsnal

New Member

Aref

New Member

Aref

New Member

threehandsnal

New Member

Aref

New Member

threehandsnal

New Member

hkh74

New Member

threehandsnal

New Member

hkh74

New Member