- ارسال ها
- 1,351
- لایک ها
- 1,322
- امتیاز
- 113
1 ببخشین این سوالو خودم طرح کردم نمیدونم چظور حل میشه!
در رابطه ی همنهشتی رو برو
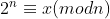 nعددی طبیعی و بزرگتر از 1 است ثابت کنید با تغییر nدر نتیجهxهم تغییر میکند
nعددی طبیعی و بزرگتر از 1 است ثابت کنید با تغییر nدر نتیجهxهم تغییر میکند
سوال من اینه آیا x بعضی اوقات صفر و بعضی اوقات توان طبیعی از 2 است (البته 1 هم محسوب میشوذ)؟اگر اینطوره اثباتش کنین اگه نه بازم اثبات کنین که اون نمیشه و مثال نقض بزنین!
فک نکنم واسه شما سوال خیلی سختی باشه بالاخره دیگه این اولین سوال نظریه ای که ذهنمو مشغول کرده
در رابطه ی همنهشتی رو برو
سوال من اینه آیا x بعضی اوقات صفر و بعضی اوقات توان طبیعی از 2 است (البته 1 هم محسوب میشوذ)؟اگر اینطوره اثباتش کنین اگه نه بازم اثبات کنین که اون نمیشه و مثال نقض بزنین!
فک نکنم واسه شما سوال خیلی سختی باشه بالاخره دیگه این اولین سوال نظریه ای که ذهنمو مشغول کرده
