سوال خيلي قشنگ...
پاسخ : سوال خيلي قشنگ...
میشه لطفا جواب سوالی که توی تاپیک http://www.irysc.com/forum/t15304-2/#post188855 مطرح کردین رو اول بذارین؟
---- دو نوشته به هم متصل شده است ----
من با استقرا حل کردم
میشه لطفا جواب سوالی که توی تاپیک http://www.irysc.com/forum/t15304-2/#post188855 مطرح کردین رو اول بذارین؟
---- دو نوشته به هم متصل شده است ----
من با استقرا حل کردم
پاسخ : سوال خيلي قشنگ...
راهنمایی:جدولی 2n+3(ستون) در 2n[SUP]2[/SUP]+5n+3(سطر)(تعداد بازی ها) بکشید. استقرا رو اینکه n درسته رو فرض کنید(فرض کنید هر بازیکن بعد از هر بازی،n+1 مسابقه استراحت میکند)،حالا برای n+1 ثابت کنید.حالا رو جدول اولیه،2 تا ستون اضافه و 4n+8 تا ستون سطر اضافه کنید.حالا برهان خلف بگیرید.
بقیه اش هم واضحه:86:
راهبر های گرامی،این راه حل درسته؟
راهنمایی:جدولی 2n+3(ستون) در 2n[SUP]2[/SUP]+5n+3(سطر)(تعداد بازی ها) بکشید. استقرا رو اینکه n درسته رو فرض کنید(فرض کنید هر بازیکن بعد از هر بازی،n+1 مسابقه استراحت میکند)،حالا برای n+1 ثابت کنید.حالا رو جدول اولیه،2 تا ستون اضافه و 4n+8 تا ستون سطر اضافه کنید.حالا برهان خلف بگیرید.
بقیه اش هم واضحه:86:
راهبر های گرامی،این راه حل درسته؟
آخرین ویرایش توسط مدیر
پاسخ : سوال خيلي قشنگ...
راه حلم اشتباهه!!!:12:
---- دو نوشته به هم متصل شده است ----
یه راه دیگه دارم:هر فرد 2n+2 بازی انجام میده. نفر اول و نفر دوم بازی افتتاحیه رو انجام میدن.نفر اول n بازی دیگه رو استراحت کنه.بنابر این نفر اول دومین بازی خودش رو تو مسابقه ی n+2 ام انجام خواهد داد و سومین رو توی 2n+3 امین.پس کلا آخرین بازی خودش رو توی2n+1)(n+1)+1) که برابره با 2n[SUP]2[/SUP]+4n+3انجام میده.از طفری نفر دومی نمیتونی بعد از هر n مسابقه استراحت کنه،چون نفر اول دوره ی n تای استراحت داشته.پش نفر دوم حداقل n+1 مسابقه دوره استراحتشه.مثل بالا این آدم بازی دومش رو توی n+3 امین انجام میده،بازی سومش رو هم توی 2n+5.پس آخرین بازیش رو هم توی 1+(n+2)(2n+1) انجام میده که میشه 2n[SUP]2[/SUP]+5n+3 امین بازی:195:
راه حلم اشتباهه!!!:12:
---- دو نوشته به هم متصل شده است ----
یه راه دیگه دارم:هر فرد 2n+2 بازی انجام میده. نفر اول و نفر دوم بازی افتتاحیه رو انجام میدن.نفر اول n بازی دیگه رو استراحت کنه.بنابر این نفر اول دومین بازی خودش رو تو مسابقه ی n+2 ام انجام خواهد داد و سومین رو توی 2n+3 امین.پس کلا آخرین بازی خودش رو توی2n+1)(n+1)+1) که برابره با 2n[SUP]2[/SUP]+4n+3انجام میده.از طفری نفر دومی نمیتونی بعد از هر n مسابقه استراحت کنه،چون نفر اول دوره ی n تای استراحت داشته.پش نفر دوم حداقل n+1 مسابقه دوره استراحتشه.مثل بالا این آدم بازی دومش رو توی n+3 امین انجام میده،بازی سومش رو هم توی 2n+5.پس آخرین بازیش رو هم توی 1+(n+2)(2n+1) انجام میده که میشه 2n[SUP]2[/SUP]+5n+3 امین بازی:195:
پاسخ : سوال خيلي قشنگ...
پاک نویسامو پیدا کردم :1: از روش جواب رو مینویسم:
در کل این تورنمنت باید تعداد
انجام شود. تورنمنت را به
روز تقسیم می‌کنیم که در هر روز
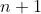بازی انجام می‌شود و بازی‌ها روی میزهای 1، 2، 3، ... و
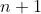به ترتیب پشت سر هم انجام می شوند. چون هر بازیکن تنها یک بازی در هر روز می‌تواند انجام دهد و در کل
بازی انجام می‌دهد، نتیجه می‌گیریم که هر بازیکن دقیقاً یک روز را استراحت میکند. میز
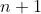را در نظر بگیرید، اگر نفرات
و
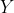در این میز بازی کنند، در روز بعد این دو تنها می‌توانند در همین میز بازی کنند، و چون هر دونفر دقیقاً یک بازی انجام می‌دهند، بنابراین یکی از این دو در این میز می‌ماند و دیگری به استراحت می‌رود (دقت کنید که هردو نفر نمی‌توانند به استراحت بروند). با همین استدلال برای میزهای
،
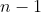، ... و 1 نتیجه می‌گیریم که در هر بازی، یک نفر روی میز باقی می‌ماند و دیگری به میز بعدی می‌رود. بدون کاسته شدن از کلیت مسئله فرض می‌کنیم که تیم بازنده روی میز می‌ماند و تیم برنده به میز بعدی می‌رود، یعنی تیم بازنده
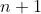بازی بعد و تیم برنده
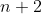بازی بعد بازی خواهد کرد (میز
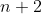را به عنوان میز استراحت در نظر می‌گیریم). اما اگر نفر
نفر
را شکست داد، همواره روی میز جلوتر از او خواهد نشست، زیرا در غیر این صورت این دو باید بار دیگر باهم بازی کنند. حال فرض کنید
و
تیم‌های میز 1 در روز اول باشند و
تیمی باشد که در روز اول استراحت میکند. بدون کاسته شدن از کلیت مسئله فرض می‌کنیم
،
را ببرد، در این صورت به وضوح مشخص است برای این منظور که
بازی اختتامیه را انجام دهد، باید همه‌ی بازی‌های خود را ببرد تا در هر مرحله یک میز جلو برود و در بازی آخر روی میز آخر باشد. فرض می‌کنیم این چنین نباشد و
برای اولین بار در روز
ام شکست بخورد. پس
در روز
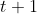ام باید بازهم روی میز
ام نشسته باشد و با فردی که در روز
ام روی میز
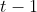ام نشسته بوده بازی کند. اما این فرد نیز باید تمامی بازی‌های خود را تا این روز برده باشد، زیرا در غیر این صورت نتیجه می‌گیریم که این فرد قبلاً با
بازی کرده است. پس این شخص در روز
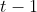ام روی میز
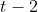، در روز
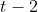ام روی میز
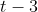، ... و در روز دوم روی میز اول باشد، پس این فرد یا
است و یا
. اما چون
و
قبلاً باهم بازی کرده اند، پس تیم مورد نظر باید
باشد و در نتیجه در روز دوم
باید
را برده باشد، در این صورت از طرفی
هیچ‌گاه از
جلو نمی‌افتد و از طرف دیگر چون
استراحت کرده پس دیگر استراحت نمی‌کند، که در این صورت
هیچ‌گاه استراحت نمی‌کند! که این تناقض است. پس فرض خلف باطل شده و تیم
همه‌ی بازی‌های خود را برده است. پس تیم
که بازی افتتاحیه را انجام داده است، بازی اختتامیه را نیز انجام داده است.
در ضمن انگشتام هم بی‌حس شده به خاطر تایپ :4:
پاک نویسامو پیدا کردم :1: از روش جواب رو مینویسم:
در کل این تورنمنت باید تعداد
در ضمن انگشتام هم بی‌حس شده به خاطر تایپ :4: