قضیه ی اساسی جبر
پاسخ : قضیه ی اساسی جبر
یه اثبات فوق العاده. گر چه به درد المپیاد نمی خوره ولی چون خیلی حد اقل برای خودم شگفت انگیزه گفتم بد نیست بگمش. اثبات رو از جایی بازنویسی می کنم.
=x^{n}+a_{n-1}x^{n-1}+...+a_{0})
برهان خلف می زنیم. فرض کنید ریشه نداره. لذا تابع پیوسته ی
 به صورت زیر در تمام نقاط قابل تعریفه.(S[SUP]1[/SUP] مرز دایره واحده)
به صورت زیر در تمام نقاط قابل تعریفه.(S[SUP]1[/SUP] مرز دایره واحده)
=\frac{P(x)}{|P(x)|})
حالا فرض کنید S دیسکی به مرکز مبدا مختصات صفحه ی مختلط و شعاع به اندازه ی کافی بزرگ R باشد. طبق قضیه ای(غیر مقدماتی) می دانیم درجه ی(عدد چرخش) f روی S صفره.
اما می دانیم اگر z عددی باشد با نرم خیلی بزرگ آنگاه
}{|P(z)|}\simeq \frac{z^{n}}{|z^{n}|}) پس اگر z نقطه ای روی مرزSباشد آنگاه این دو عدد مختلط که هر دو روی دایره واحد اند خیلی به هم نزدیکند. اما به راحتی می توان دید عدد چرخش سمت راست رابطه یعنی
پس اگر z نقطه ای روی مرزSباشد آنگاه این دو عدد مختلط که هر دو روی دایره واحد اند خیلی به هم نزدیکند. اما به راحتی می توان دید عدد چرخش سمت راست رابطه یعنی
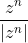 برابر n است. که با فرض صفر بودن عدد چرخش سمت چپ که همان f است در تناقض است و اثبات تمام است.
برابر n است. که با فرض صفر بودن عدد چرخش سمت چپ که همان f است در تناقض است و اثبات تمام است.
پ.ن: عدد چرخش یا درجه ی یه تابع از مرز یه دایره به مرز یه دایره ی دیگه به طور نادقیق و شهودی یعنی وقتی x روی دامنه یک دور می چرخه اونوقت f(x) روی برد چند دور میچرخه.
یه اثبات فوق العاده. گر چه به درد المپیاد نمی خوره ولی چون خیلی حد اقل برای خودم شگفت انگیزه گفتم بد نیست بگمش. اثبات رو از جایی بازنویسی می کنم.
برهان خلف می زنیم. فرض کنید ریشه نداره. لذا تابع پیوسته ی
حالا فرض کنید S دیسکی به مرکز مبدا مختصات صفحه ی مختلط و شعاع به اندازه ی کافی بزرگ R باشد. طبق قضیه ای(غیر مقدماتی) می دانیم درجه ی(عدد چرخش) f روی S صفره.
اما می دانیم اگر z عددی باشد با نرم خیلی بزرگ آنگاه
پ.ن: عدد چرخش یا درجه ی یه تابع از مرز یه دایره به مرز یه دایره ی دیگه به طور نادقیق و شهودی یعنی وقتی x روی دامنه یک دور می چرخه اونوقت f(x) روی برد چند دور میچرخه.
آخرین ویرایش توسط مدیر
- ارسال ها
- 1,326
- لایک ها
- 998
- امتیاز
- 113
پاسخ : قضیه ی اساسی جبر
شما اسم اینو میزارید اثبات؟؟!
"با توجه به یک قضیه (غیر مقدماتی)" یعنی چی؟
هر چیزی استفاده میکنید باید اثیات کنید..یا حداقلش اسمشو بگین!!
قضیه ی غیر مقدماتی یعنی چی؟!
از اول میگیمم خب این قضیه یک قضیه ی غیر مقدماتیه و حکم حابت است!!:116::116:
یه اثبات فوق العاده. گر چه به درد المپیاد نمی خوره ولی چون خیلی حد اقل برای خودم شگفت انگیزه گفتم بد نیست بگمش. اثبات رو از جایی بازنویسی می کنم.
=x^{n}+a_{n-1}x^{n-1}+...+a_{0})
برهان خلف می زنیم. فرض کنید ریشه نداره. لذا تابع پیوسته ی
 به صورت زیر در تمام نقاط قابل تعریفه.(S[SUP]1[/SUP] مرز دایره واحده)
به صورت زیر در تمام نقاط قابل تعریفه.(S[SUP]1[/SUP] مرز دایره واحده)
=\frac{P(x)}{|P(x)|})
حالا فرض کنید S دیسکی به مرکز مبدا مختصات صفحه ی مختلط و شعاع به اندازه ی کافی بزرگ R باشد. طبق قضیه ای(غیر مقدماتی) می دانیم درجه ی(عدد چرخش) f روی S صفره.
اما می دانیم اگر z عددی باشد با نرم خیلی بزرگ آنگاه
}{|P(z)|}\simeq \frac{z^{n}}{|z^{n}|}) پس اگر z نقطه ای روی مرزSباشد آنگاه این دو عدد مختلط که هر دو روی دایره واحد اند خیلی به هم نزدیکند. اما به راحتی می توان دید عدد چرخش سمت راست رابطه یعنی
پس اگر z نقطه ای روی مرزSباشد آنگاه این دو عدد مختلط که هر دو روی دایره واحد اند خیلی به هم نزدیکند. اما به راحتی می توان دید عدد چرخش سمت راست رابطه یعنی
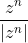 برابر n است. که با فرض صفر بودن عدد چرخش سمت چپ که همان f است در تناقض است و اثبات تمام است.
برابر n است. که با فرض صفر بودن عدد چرخش سمت چپ که همان f است در تناقض است و اثبات تمام است.
پ.ن: عدد چرخش یا درجه ی یه تابع از مرز یه دایره به مرز یه دایره ی دیگه به طور نادقیق و شهودی یعنی وقتی x روی دامنه یک دور می چرخه اونوقت f(x) روی برد چند دور میچرخه.
برهان خلف می زنیم. فرض کنید ریشه نداره. لذا تابع پیوسته ی
حالا فرض کنید S دیسکی به مرکز مبدا مختصات صفحه ی مختلط و شعاع به اندازه ی کافی بزرگ R باشد. طبق قضیه ای(غیر مقدماتی) می دانیم درجه ی(عدد چرخش) f روی S صفره.
اما می دانیم اگر z عددی باشد با نرم خیلی بزرگ آنگاه
پ.ن: عدد چرخش یا درجه ی یه تابع از مرز یه دایره به مرز یه دایره ی دیگه به طور نادقیق و شهودی یعنی وقتی x روی دامنه یک دور می چرخه اونوقت f(x) روی برد چند دور میچرخه.
"با توجه به یک قضیه (غیر مقدماتی)" یعنی چی؟
هر چیزی استفاده میکنید باید اثیات کنید..یا حداقلش اسمشو بگین!!
قضیه ی غیر مقدماتی یعنی چی؟!
از اول میگیمم خب این قضیه یک قضیه ی غیر مقدماتیه و حکم حابت است!!:116::116:
پاسخ : قضیه ی اساسی جبر
بله حق با شماست. یکم در مورد قضیه می نویسم.
شاید درست نبود بنویسم غیر مقدماتی. حالا که می بینم اثبات اونقدر هم غیر مقدماتی نیست. اما خیلی خر کاری داره. برا همین هم اثباتش رو نمی نویسم ولی چون خیلی اصرار دارین انشاالله اگه زنده بودم یه روز دیگه سر فرصت اثباتشو می ذارم.
قضیه متاسفانه اسمشو نمی دونم)
متاسفانه اسمشو نمی دونم)
تابع
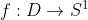 پیوسته است که D دیسکه. در این صورت تابع f رو اگه فقط روی S[SUP]1[/SUP] در نظر بگیریم این تابع عدد چرخشش صفره.
پیوسته است که D دیسکه. در این صورت تابع f رو اگه فقط روی S[SUP]1[/SUP] در نظر بگیریم این تابع عدد چرخشش صفره.
شما اسم اینو میزارید اثبات؟؟!
"با توجه به یک قضیه (غیر مقدماتی)" یعنی چی؟
هر چیزی استفاده میکنید باید اثیات کنید..یا حداقلش اسمشو بگین!!
قضیه ی غیر مقدماتی یعنی چی؟!
از اول میگیمم خب این قضیه یک قضیه ی غیر مقدماتیه و حکم حابت است!!:116::116:
"با توجه به یک قضیه (غیر مقدماتی)" یعنی چی؟
هر چیزی استفاده میکنید باید اثیات کنید..یا حداقلش اسمشو بگین!!
قضیه ی غیر مقدماتی یعنی چی؟!
از اول میگیمم خب این قضیه یک قضیه ی غیر مقدماتیه و حکم حابت است!!:116::116:
شاید درست نبود بنویسم غیر مقدماتی. حالا که می بینم اثبات اونقدر هم غیر مقدماتی نیست. اما خیلی خر کاری داره. برا همین هم اثباتش رو نمی نویسم ولی چون خیلی اصرار دارین انشاالله اگه زنده بودم یه روز دیگه سر فرصت اثباتشو می ذارم.
قضیه
تابع
پاسخ : قضیه ی اساسی جبر
ابتدا حکم را برای
 ثابت می کنیم
ثابت می کنیم
فرض کنید
 درجه
درجه
 باشد.
باشد.
فرض کنید
 . با استقرا روی
. با استقرا روی
 ثابت کنید که چند جمله ای حداقل یک ریشه مختلط دارد.
ثابت کنید که چند جمله ای حداقل یک ریشه مختلط دارد.
در این قسمت باید یه چندجمله ای با درجه ی
 از روی چندجمله ای اولیه بسازید و از فرض استقرا استفاده کنید.
از روی چندجمله ای اولیه بسازید و از فرض استقرا استفاده کنید.
سپس این حکم را به
 ریط دهید.
ریط دهید.
ابتدا حکم را برای
فرض کنید
فرض کنید
در این قسمت باید یه چندجمله ای با درجه ی
سپس این حکم را به
آخرین ویرایش توسط مدیر
