نامساوی ( انتخابی تیم رومانی 1999 )

farid_frd · 1389/1/30

برای اعداد مثبت

$x_{1},x_{2},...,x_{n}$

که

$x_{1}x_{2}...x_{n}=1$

ثابت کنید :

$\sum_{i=1}^{n}\frac{1}{n-1+x_{i}}\leq 1$

farid_frd · 1389/2/1

حل نکردین تا آخرش خودم تونستم حل کنم :

دو طرف نامساوی را در

$n-1$

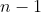ضرب می کنیم سپس به دو طرف مقدار

$1$

را اضافه می کنیم حکم به این صورت در می آید :

$n-\sum_{i=1}^{n}\frac{n-1}{n-1+x_{i}}\geq 1$

که اگر

$n$

را به صورت مجموع

$n$

تا

$1$

بنویسیم و به داخل سیگما ببریم و عبارت را ساده کنیم حکم به این صورت در می آید :

$\sum_{i=1}^{n}\frac{x_{i}}{n-1+x_{i}}\geq 1$

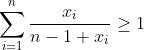که با استفاده ار کوشی :

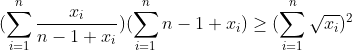$(\sum_{i=1}^{n}\frac{x_{i}}{n-1+x_{i}})(\sum_{i=1}^{n}n-1+x_{i})\geq (\sum_{i=1}^{n}\sqrt{x_{i}})^{2}$

که اگر قرار دهیم :

$\sqrt{x_{i}}=y_{i}$

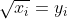باید ثابت کنیم :

$\frac{(\sum_{i=1}^{n}y_{i})^{2}}{\sum_{i=1}^{n}n-1+y_{i}^{2}}\geq 1$

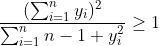یا به عبارتی :

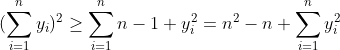$(\sum_{i=1}^{n}y_{i})^{2}\geq \sum_{i=1}^{n}n-1+y_{i}^{2}=n^{2}-n+\sum_{i=1}^{n}y_{i}^{2}$

پس کافی است ثابت کنیم :

$2\sum y_iy_j\geq n(n-1)$

از طرفی بنابر حسابی هندسی و با توجه به اینکه حاصل ضرب

$y_{i}$

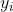ها برابر واحد است داریم :

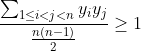$\frac{\sum_{1\leq i<j<n} y_iy_j}{\frac{n(n-1)}2}\geq1$

پس حکم ثابت شد

M_Sharifi · 1389/2/1

آخر اثباتت رو یه بار دیگه وارد کن.

farid_frd · 1389/2/2

ببخشید نمیدونم چرا هر چی اصلاحش میکنم فرقی نمیکنه لینکشو میذارم اینجا:
تصویر اول :
http://www.2shared.com/fadmin/12739343/16121186/Capture.JPG.html
تصویر دوم :
http://www.2shared.com/fadmin/12739359/efdcc9d9/Capture2.JPG.html

farid_frd · 1389/2/2

هــــــــــــــــــــــــــــــــــــــوراااااااااااااااااااااااااااااااااا

بالاخره تونستم یه جوری واردش کنم

M_Sharifi · 1389/2/2

یه راه حل دیگه.
بعد از مخرج مشترک گرفتن و طرفین وسطین، باید ثابت کنیم عبارت

[center:ec9799b4ac]

$1+(n-1)^n-n(n-1)^{n-1}+\sum_{k=1}^{n-1}\left((n-1)^{n-k}-(n-1-k)(n-1)^{n-k-1}\right)\sum x_{i_1}x_{i_2}\cdots x_{i_k}$

نامنفی است. طبق نابرابری میانگین حسابی هندسی، این عبارت بزرگ تر یا مساوی

$1+(n-1)^n-n(n-1)^{n-1}+\sum_{k=1}^{n-1}\left((n-1)^{n-k}-(n-1-k)(n-1)^{n-k-1}\right){n\choose k}$

است، که مقدار این عبارت برابر صفر است (چرا؟).

[/center:ec9799b4ac]

نامساوی ( انتخابی تیم رومانی 1999 )

farid_frd

New Member

farid_frd

New Member

M_Sharifi

راهبر ریاضی

farid_frd

New Member

farid_frd

New Member

M_Sharifi

راهبر ریاضی