قسمت الف)
[center:dd914686b3]
 [/center:dd914686b3]
[/center:dd914686b3]
قسمت ب)
راه حل اول.
فرض می کنیم
 . بنابراین
. بنابراین
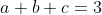 و باید ثابت کنیم
و باید ثابت کنیم
[center:dd914686b3]


[center:dd914686b3]
قسمت ب)
راه حل اول.
فرض می کنیم
[center:dd914686b3]
داریم
چراکه
 . بنابراین
. بنابراین

راه حل دوم. کافی است ثابت کنیم

طبق نابرابری کوشی-شوارتز،

طبق نابرابری کوشی-شوارتز،
بنابراین کافی است ثابت کنیم

این نابرابری هم بعد از ساده شدن به صورت

در می آید که از جمع بستن نابرابری های
 و
و
 [/center:dd914686b3]به دست می آید.
[/center:dd914686b3]به دست می آید.




