C
پاسخ تشریحی بیست و یکمین دوره
[hr:06e4957a23]سؤال یکم)
ده توپ داریم که روی آن‌ها اعداد ۱ تا ۱۰ ...
پاسخ: گزینه‌ی (ج) (جواب=۲)
چون مجموع اعداد باید ۵۵ باشه، مجموعه‌ی دوم نمیتونه درست باشه.
مجموعه‌ی چهارم هم نمیتونه درست باشه. چون اگر ۳ تا ۵ داشته باشیم، ۳ تا از مجموعه‌ها باید (۱و۴) و (۲و۳) و (۵) باشند. و حالا هم حداکثر یک مجموعه‌ی دیگر با مجموع ۱۰ می‌تونیم بسازیم، نه ۴ تا!
مجموعه‌ی اول را اینطور می‌سازیم: (۱و۸) و (۴و۶) و (۲و۹) و (۵و۷) و (۳و۱۰)
مجموعه‌ی سوم را هم اینطور می‌سازیم: (۱و۴) و (۵و۷) و (۳و۶و۸) و (۲و۹و۱۰)
[hr:06e4957a23]سؤال دوم)
۱۵ گل‌دان خالی را در یک ...
پاسخ: گزینه‌ی (ب) (جواب=۱۲۶)
باید تعداد جواب‌های معادله‌ی
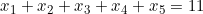را پیدا کنیم باشرط
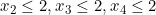. که برابر با تعداد جواب‌های معادله‌ی
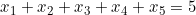در مجموعه اعداد صحیح نامنفی است که این هم برابر است با:
.
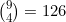[hr:06e4957a23]سؤال سوم)
شکل مقابل از ۱۵ توپ و ۳۰ میله تشکیل شده ...
پاسخ: گزینه‌ی (د) (جواب=۶)
[JUSTIFY]با برهان خلف ثابت می‌کنیم که حذف حداقل ۶ توپ برای رسیدن به هدف بزرگمون! لازمه. بنابراین فرض کنید که ۵ (منظورم کمتر از ۶ است!) دانه توپ را حذف کرده‌ایم و هیچ مشکلی هم پیش نیومده و همه خوشحالیم و ماه هم هنوز دور زمین می‌گرده! طبق شکل زیر، توپ‌ها را ۳ دسته می‌کنیم. در یکی از این سه دسته ۰ یا ۱ توپ را حذف کرده‌ایم (چرا؟). صفر تا هم نمیشه(چرا؟)، پس از یکی از سه دسته دقیقاْ ۱ توپ حذف شده. فرض کنید از دسته‌ی قرمزرنگ ۱ توپ حذف شده.[/JUSTIFY][center:06e4957a23]
[JUSTIFY]این تنها توپی که از قرمزها حذف شده، حتماْ باید توپ مشخص شده در شکل زیر باشه (چرا؟).[/JUSTIFY][/center:06e4957a23][center:06e4957a23]
[JUSTIFY]حالا روشنه که هیچ کدوم از توپ‌های آبی، سبز، زرد یا قرمز در شکل بالا نباید حذف شوند (چرا؟ گفتم که روشنه!). حالا توپ سبز را در نظر بگیرید. دو تا توپ مجاور به اسم‌های آبی و زرد داره و دیگه نباید هیچ توپ مجاوری داشته باشه. پس بقیه‌ی مجاورهای توپ سبز حتماْ باید حذف شده بشوند و چنین بلایی سر شکل میاد:[/JUSTIFY]
[/center:06e4957a23]تا حالا ۴ تا توپ حذف شده. باز هم روشنه که دو توپ دیگه حتماْ باید حذف بشه که در مجموع میشود ۶ توپ. تناقض!! پس با ۵ توپ یا کمتر نمیشه به هدف بزرگ رسید و حذف حداقل ۶ توپ لازمه. شکل‌های زیر نشون می‌دهند که کافی هم هست.
[center:06e4957a23]
[/center:06e4957a23][hr:06e4957a23]سؤال چهارم)
علی می‌خواهد تعدادی عدد از چپ به راست ...
پاسخ: گزینه‌ی (هـ) (جواب=۸)
کافیه یه نمودار درختی بکشیم و نشون بدیم که بعد از هر عدد چه عددهایی میتونه بیاد. هرجا هم به عدد بزرگتر از ۱۰ برسیم دیگه لازم نیست ادامه بدیم چون بقیه‌ی مراحل یکتاست. پس طبق نمودار زیر جواب میشه ۸.
[center:06e4957a23]
[/center:06e4957a23][hr:06e4957a23]سؤال پنجم)
به چند طریق می‌توان خانه‌های یک جدول ۳ در ۵ را ...
پاسخ: گزینه‌ی (الف) (جواب=۳۲۵۷۷)
[JUSTIFY]ابتدا تعداد رنگ‌آمیزی‌هایی که شکل موردنظر در آن‌ها یافت میشود را می‌شماریم. تعداد رنگ‌آمیزی‌هایی که شکل داده‌شده در مربع ۳ در ۳ سمت چپ باشد برابر با
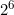است. اگر سمت راست باشد نیز همین‌طور. حالتی که هم در سمت راست و هم در سمت چپ باشد را دو بار شمردیم. پس یکی کم می‌کنیم. تعداد رنگ‌آمیزی‌هایی که شکل موردنظر در مربع ۳ در ۳ وسطی باشد هم
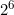است. پس تعداد رنگ‌آمیزی‌های نامطلوب
است. اگر این را از کل تعداد حالات کم کنیم میشود:
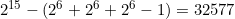[/JUSTIFY][hr:06e4957a23][JUSTIFY]سؤال ششم)
می‌خواهیم توپ‌های شکل مقابل را با رنگ‌های سبز، زرد و قرمز رنگ‌آمیزی کنیم ...
پاسخ: گزینه‌ی (د) (جواب=۱۲)
سه توپ زرد در این شکل باید همرنگ باشند. سه توپ قرمز هم همین‌طور. ابتدا رنگ سه توپ زرد را تعیین می‌کنیم (۳ حالت) و بعد رنگ سه توپ قرمز را تعیین می‌کنیم (۲ حالت) و بعد رنگ توپ سبز (۲ حالت) و بعد رنگ توپ آبی (۱ حالت). پس جواب طبق اصل ضرب میشه ۳*۲*۲ یعنی ۱۲
[center:06e4957a23]
[/center:06e4957a23][hr:06e4957a23]سؤال هفتم)
دستگاهی داریم که یک جدول ۴ * ۴ را ...
پاسخ: سؤال غلط است!
به ازای هر جدول ورودی هرگز دستگاه چنین خروجی‌ای تولید نمی‌کند! (چرا؟)
[hr:06e4957a23]اول یه توضیح در مورد سؤالهای ۸ تا ۱۱ می‌نویسم.
ابتدا ببینیم کشور k+۱-منگولیا را چطور می‌تونیم بسازیم.
برای ساختن کشور k+۱-منگولیا کافیه دو تا k-منگولیا را کنار هم بگذاریم و شهرهای متناظر بین این دو کشور را به هم وصل کنیم.و در کشور اولی در ابتدای مبنای دوی شماره‌ی هرشهر یک صفر بنویسیم و در کشور دوم در ابتدای مبنای دوی شماره هر شهر رقم یک را بنویسیم.
[hr:06e4957a23]سؤال هشتم)
در کشور ۴-منگولیا ...
پاسخ: گزینه‌ی (الف) (جواب=۲)
اول شهرهای دو تا ۳-منگولیا را با دو رنگ همانطور که خواسته شده رنگ می‌کنیم و بعد به همون روشی که بالا گفتم دو تا از این‌ها را کنار هم می‌گذاریم و رنگ‌های یکی را معکوس می‌کنیم و شهرهای متناظر را به هم وصل می‌کنیم. پس رنگ‌آمیزی با دو رنگ ممکنه. حالا چطور اون ۳-منگولیاها رو رنگ کنیم؟ خب، دو تا ۲-منگولیا را رنگ می‌کنیم و کنار هم می‌گذاریم و ... (در واقع راه حل با استقرا بود)
[hr:06e4957a23]سؤال نهم)
حداقل با چند رنگ می‌توانیم به هریک از جاده‌های ...
پاسخ: گزینه‌ی (ج) (جواب=۷)
باز هم از استقرا استفاده می‌کنیم. جاده‌های دو تا ۶-منگولیا را با ۶ رنگ، رنگ می‌کنیم و وقتی شهرهای متناظر را به هم وصل کردیم، جاده‌های جدید را با رنگ هفتم، رنگ می‌کنیم. پس با ۷ رنگ ممکنه. از طرفی با ۶ رنگ و یا کمتر ممکن نیست. چون به هر شهر ۷ جاده وصله و این باعث میشه حداقل ۷ رنگ نیاز باشه.
[hr:06e4957a23]سؤال دهم)
در کشور ۱۰-منگولیا حداقل چند جاده را باید ...
پاسخ: گزینه‌ی (د) (جواب=
)
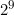ابتدا دقت کنید که هر جاده دقیقاْ دو شهر را می‌بیند. پس تعداد جاده‌هایی که گل‌کاری می‌کنیم حداقل باید به اندازه‌ی نصف تعداد شهرها باشه. پس حداقل
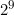جاده را باید گل‌کاری کنیم. این تعداد کافی هم هست. باز هم با استقرا ثابت می‌کنیم. دو تا ۹-منگولیا را گل‌کاری می‌کنیم و کنار هم می‌گذاریم و بین شهرهای متناظر جاده می‌کشیم. دیگه هم نیاز به گل‌کاری نیست. در هر کدوم از ۹-منگولیاها
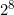تا جاده گل‌کاری شده بود که در مجموع میشه
.
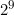[hr:06e4957a23]سؤال یازدهم)
در کشور ۱۱-منگولیا حداقل چند شهر را باید چراغانی کنیم ...
[JUSTIFY]پاسخ: گزینه‌ی (هـ) (جواب=
)
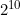۱۱-منگولیا،
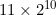جاده دارد (چرا؟) و هر شهر به ۱۱ شهر دیگر جاده دارد. پس هر شهری که چراغانی شود، مشکل حداکثر ۱۱ جاده حل میشود. بنابراین حدقال
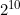شهر باید چراغانی شود. برای اثبات این که چراغانی کردن این تعداد شهر کافی‌است، یاز هم از استقرا استفاده می‌کنیم. ۲ تا ۱۰-منگولیا را چراغانی می‌کنیم و کنار هم قرار می‌دهیم. در یکی از آن‌ها شهرهای چراغانی را برعکس می‌کنیم (یعنی اگر شهری چراغانی بود، دیگر نیست و اگر نبود، حالا هست!) و بین شهرهای متناظر جاده می‌سازیم. هرکدام از ۱۰-منگولیاها
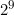شهر چراغانی دارد که در مجموع میشود
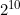شهر چراغانی.
[hr:06e4957a23][/JUSTIFY]سؤال دوازدهم)
در یک سطر دل‌خواه حداکثر چند سکه ممکن است ...
پاسخ: گزینه‌ی (هـ) (جواب=۱۶)
کافی‌است در سطر اول ۱۶ سکه با عدد ۱ قرار دهیم.
[hr:06e4957a23]سؤال سیزدهم)
فرض کنید که تمام سکه‌های این جدول را برمی‌داریم و ...
پاسخ: گزینه‌ی (الف) (جواب=۱)
همه‌ی اعداد هر سطر متفاوتند. زیرا اگر عددی مثل ۳ دو بار در سطری بیاید، طبق شکل حداقل ۱۷ تا ۳ داریم، ولی نداریم!
[center:06e4957a23]
[/center:06e4957a23][hr:06e4957a23]سؤال چهاردهم)
فرض کنید که جدول اولیه را مطابق شکل زیر ...
پاسخ: گزینه‌ی (د) (جواب=۷)
به شکل نگاه کنید. در سطر دوم ۷ تا عدد ۲ داریم.
[center:06e4957a23]
[/center:06e4957a23]با کمی دقت متوجه می‌شوید که ۸ عدد یکسان در یک سطر امکان ندارد.
[hr:06e4957a23]سؤال پانزدهم)
علی ۳۱ کارت با شماره‌های ۱ تا ۳۱ دارد ...
پاسخ: گزینه‌ی (الف) (جواب=۳۰)
ابتدا دقت کنید که اعداد ۱ تا ۳۱ در مبنای دو، حداکثر ۵ رقمی هستند. پس XOR هر دو تا از آن‌ها هم حداکثر ۵ رقمی است و این یعنی بزرگترین XOR نمی‌تواند از ۳۱ بزرگتر باشد. پس گزینه‌ی (هـ) رد میشود. از طرفی ۳۱ هم ممکن نیست. چون اگر خروجی دستگاه ۳۱ باشد، در دو عدد ورودی، ارقام متناظر با هم متفاوتند (چرا؟). در این صورت مجموع این دو عدد، ۳۱ میشود (چرا؟) ولی مسئله گفته است که مجموع دو عدد ورودی باید ۳۲ باشد. حالا ببینیم چرا خروجی ۳۰ ممکن است. کافی است دو عدد ۱ و ۳۱ را به دستگاه بدهیم تا خروجی ۳۰ باشد.
[hr:06e4957a23]سؤال شانزدهم)
برنامه‌ی زیر چه عددی را چاپ خواهد کرد ...
پاسخ: گزینه‌ی (ج) (جواب=۱۳۹۰)
یگ نکته‌ی مهم در مورد XOR وجود دارد وآن نکته این است که ترتیب در XOR اهمیت ندارد. مثلاْ
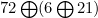با
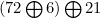برابر است (
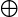را نماد XOR دو عدد فرض کنید).
اگر دقت کنید در این برنامه، در پایان خواهیم داشت:
[center:06e4957a23]
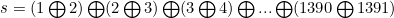[/center:06e4957a23]
و طبق نکته‌ی بالا داریم:
[center:06e4957a23]
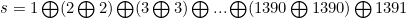[/center:06e4957a23]
می‌دانیم XOR دو عدد مساوی صفر است و صفر نیز در XOR بی‌تأثیر است. پس :
[center:06e4957a23]
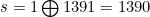[/center:06e4957a23][hr:06e4957a23]سؤال هفدهم)
پاسخ: گزینه‌ی (ج) (جواب=۵۶۴)
خروجی برابر با
خواهد بود. این هم با مقداری محاسبه برابر ۵۶۴ است.
[hr:06e4957a23]سؤال هجدهم)
شش مکعب چند وضعیت شامل دقیقاْ ...
پاسخ: گزینه‌ی (ب) (جواب=۱۸۰۰ و ۱۲۰۰)
برای ساختن یک وضعیت با دو برج، کافی‌است یک جایگشت از اعداد ۱ تا ۶ بسازیم (!۶ حالت) و از یکی از ۵ جای ممکن آن را دو قسمت کنیم (۵ حالت). هر وضعیت را ۲ بار شمردیم پس تعداد وضعیت‌ها با دو برج برابر است با:
[center:06e4957a23]
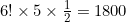.[/center:06e4957a23]در مورد ۳ برج هم باید جایگشت را ۳ قسمت کنیم( حالت). در این صورت هر وضعیت را !۳ بار شمرده ایم. پس تعداد وضعیت‌ها با ۳ برج برابر است با:
[center:06e4957a23]
.
[hr:06e4957a23][JUSTIFY]سؤال نوزدهم)
یک «حرکت» شامل برداشتن بالاترین مکعب ...
پاسخ: گزینه‌ی (د) (جواب=۷ صعودی، ۷ نزولی)
این مسئله به توضیح زیادی نیاز ندارد. کافی است حرکت‌هایی که حتماْ باید انجام شوند را پیدا کنید و ...[/JUSTIFY][/center:06e4957a23]
[hr:06e4957a23]سؤال بیستم)
حداقل میزان K چقدر باید باشد که ...
پاسخ: گزینه‌ی (ب) (جواب=۱۰)
ابتدا دقت کنید که از هر وضعیتی با حداکثر ۱۰ حرکت می‌توان به هر وضعیت دیگر رسید. چون با حداکثر ۵ حرکت می‌توان همه‌ی برج‌ها را روی میز قرار داد و با حداکثر ۵ حرکت دیگر می‌توان هر حالت دیگر را ساخت. حال با مثالی نشان می‌دهیم که ۱۰ حرکت، حداقل تعداد حرکت مورد نیاز است. به شکل زیر نگاه کنید. برای تبدیل شکل سمت چپ به شکل سمت راست حداقل ۱۰ حرکت لازم است. پس جواب مسئله ۱۰ است.
[center:06e4957a23]
[/center:06e4957a23]
[hr:06e4957a23]سؤال بیست و یکم)
فرض کنید وضعیت راه‌های کشور طوری است که ...
پاسخ: گزینه‌ی (الف) (جواب=۲)
بدون شرح!
[center:06e4957a23]
[/center:06e4957a23][hr:06e4957a23]سؤال بیست و دوم)
فرض کنید مقصد مسیرهایی استقلالی است که ...
پاسخ: گزینه‌ی (ب) (جواب=۱۳۸۹)
از برهان خلف استفاده می‌کنیم. فرض کنید این کشور کمتر از ۱۳۸۹ شهر داشته باشد. حالا مسیری را در نظر بگیرید که از تعداد زیادی جاده خاکی تشکیل شده (جاده آسفالت ندارد). در این صورت بعد از عبور از ۱۳۸۸ امین جاده‌ی خاکی به شهری می‌رسیم که قبلاْ آن‌جا بوده‌ایم (چرا؟) و پرسپولیسی هم هست (چرا؟). در عبور از جاده خاکی بعدی به یک شهر استقلالی می‌رسیم و قبلاْ هم در آن نبوده‌ایم. ولی ممکن نیست که قبلاْ در این شهر استقلالی نبوده باشیم. چون گفتیم که در آن شهر پرسپولیسی قبلی، قبلاْ بوده‌ایم. پس بعد از آن حتماْ به این شهر استقلالی رفته‌ایم.
حالا باید یک مثال با ۱۳۸۹ شهر پیدا کنیم. کافی است شهرها را دور یک دایره بچینیم و به ترتیب با جاده خاکی به هم وصل کنیم. هر شهر هم با جاده آسفالت به خودش وصل میشود.
[hr:06e4957a23]سؤال بیست و سوم)
فرض کنید مقصد مسیر تنها و تنها وقتی ...
پاسخ: گزینه‌ی (ب) (جواب=۳۱)
فعلاْ حوصله‌ی اثباتش رو ندارم. فقط مثال را ببینید:
[center:06e4957a23]
[/center:06e4957a23][hr:06e4957a23]سؤال بیست و چهارم)
ابتدا در یک سالن ۳*۳ ...
پاسخ: گزینه‌ی (هـ)
بدون شرح!
[center:06e4957a23]
[/center:06e4957a23][hr:06e4957a23]سؤال بیست و پنجم)
فرایند سؤال قبل را در یک سالن ۴*۴ ...
پاسخ: گزینه‌ی (ب)
همه‌ی گزینه‌ها ۴ تا ۱ دارند ولی (ب) ۵ تا ۱ دارد.
[hr:06e4957a23]سؤال بیست و ششم)
فراین سؤال قبل را در یک سالن ۴*۴ ...
پاسخ: گزینه‌ی (الف)
بدون شرح!
البته راه ساده تر هم برای حل داره. ولی برای نوشتن این ساده ترین راهه :
[center:06e4957a23]
[/center:06e4957a23][hr:06e4957a23]سؤال بیست و هفتم)
فرض می‌کنیم اگر دو عدد ورودی ...
پاسخ: گزینه‌ی (هـ)
نمی‌دونم چه‌طوری باید توضیح بدم. چون معلومه که این برنامه، عدد را در مبنای دو معکوس می‌کند.
[hr:06e4957a23]سؤال بیست و هشتم)
اگر ورودی برنامه مقدار X باشد ...
پاسخ: گزینه‌ی (هـ) (جواب = ۱۲۳)
۴۴۴ در مبنای ۲ میشود ۱۱۰۱۱۱۱۰۰ و طبق سؤال قبل خروجی برنامه در مبنای دو میشود ۱۱۱۱۰۱۱ که برابر با ۱۲۳ است.
[hr:06e4957a23]سؤال بیست‌ونهم)
عدد A را زیبا می‌نامیم اگر ...
پاسخ: گزینه‌ی (ج) (جواب=۹)
اعداد زیبا:
۱۰۱۱
۱۰۱۱۱
۱۰۰۱۱
۱۰۰۰۱۱
۱۰۰۱۱۱
۱۰۱۱۱۱
۱۰۱۰۱۱
۱۱۰۱۱۱
۱۰۰۱۰۱
[hr:06e4957a23]سؤال سیم)
چند تا از اعداد بین ...
پاسخ: گزینه‌ی (ب) (جواب=۹۹۲)
باید تعداد اعداد زیبای ۱۳ رقمی (در مبنای دو) را بشماریم.
محاسبه‌اش خیلی آسونه و توضیح راه حل در این‌جا طولانی میشه. پس فقط جواب رو ببینید:
[center:06e4957a23]
[hr:06e4957a23]سؤال یکم)
ده توپ داریم که روی آن‌ها اعداد ۱ تا ۱۰ ...
پاسخ: گزینه‌ی (ج) (جواب=۲)
چون مجموع اعداد باید ۵۵ باشه، مجموعه‌ی دوم نمیتونه درست باشه.
مجموعه‌ی چهارم هم نمیتونه درست باشه. چون اگر ۳ تا ۵ داشته باشیم، ۳ تا از مجموعه‌ها باید (۱و۴) و (۲و۳) و (۵) باشند. و حالا هم حداکثر یک مجموعه‌ی دیگر با مجموع ۱۰ می‌تونیم بسازیم، نه ۴ تا!
مجموعه‌ی اول را اینطور می‌سازیم: (۱و۸) و (۴و۶) و (۲و۹) و (۵و۷) و (۳و۱۰)
مجموعه‌ی سوم را هم اینطور می‌سازیم: (۱و۴) و (۵و۷) و (۳و۶و۸) و (۲و۹و۱۰)
[hr:06e4957a23]سؤال دوم)
۱۵ گل‌دان خالی را در یک ...
پاسخ: گزینه‌ی (ب) (جواب=۱۲۶)
باید تعداد جواب‌های معادله‌ی
[hr:06e4957a23]سؤال سوم)
شکل مقابل از ۱۵ توپ و ۳۰ میله تشکیل شده ...
پاسخ: گزینه‌ی (د) (جواب=۶)
[JUSTIFY]با برهان خلف ثابت می‌کنیم که حذف حداقل ۶ توپ برای رسیدن به هدف بزرگمون! لازمه. بنابراین فرض کنید که ۵ (منظورم کمتر از ۶ است!) دانه توپ را حذف کرده‌ایم و هیچ مشکلی هم پیش نیومده و همه خوشحالیم و ماه هم هنوز دور زمین می‌گرده! طبق شکل زیر، توپ‌ها را ۳ دسته می‌کنیم. در یکی از این سه دسته ۰ یا ۱ توپ را حذف کرده‌ایم (چرا؟). صفر تا هم نمیشه(چرا؟)، پس از یکی از سه دسته دقیقاْ ۱ توپ حذف شده. فرض کنید از دسته‌ی قرمزرنگ ۱ توپ حذف شده.[/JUSTIFY][center:06e4957a23]
[JUSTIFY]این تنها توپی که از قرمزها حذف شده، حتماْ باید توپ مشخص شده در شکل زیر باشه (چرا؟).[/JUSTIFY][/center:06e4957a23][center:06e4957a23]
[JUSTIFY]حالا روشنه که هیچ کدوم از توپ‌های آبی، سبز، زرد یا قرمز در شکل بالا نباید حذف شوند (چرا؟ گفتم که روشنه!). حالا توپ سبز را در نظر بگیرید. دو تا توپ مجاور به اسم‌های آبی و زرد داره و دیگه نباید هیچ توپ مجاوری داشته باشه. پس بقیه‌ی مجاورهای توپ سبز حتماْ باید حذف شده بشوند و چنین بلایی سر شکل میاد:[/JUSTIFY]
[center:06e4957a23]
علی می‌خواهد تعدادی عدد از چپ به راست ...
پاسخ: گزینه‌ی (هـ) (جواب=۸)
کافیه یه نمودار درختی بکشیم و نشون بدیم که بعد از هر عدد چه عددهایی میتونه بیاد. هرجا هم به عدد بزرگتر از ۱۰ برسیم دیگه لازم نیست ادامه بدیم چون بقیه‌ی مراحل یکتاست. پس طبق نمودار زیر جواب میشه ۸.
[center:06e4957a23]
به چند طریق می‌توان خانه‌های یک جدول ۳ در ۵ را ...
پاسخ: گزینه‌ی (الف) (جواب=۳۲۵۷۷)
[JUSTIFY]ابتدا تعداد رنگ‌آمیزی‌هایی که شکل موردنظر در آن‌ها یافت میشود را می‌شماریم. تعداد رنگ‌آمیزی‌هایی که شکل داده‌شده در مربع ۳ در ۳ سمت چپ باشد برابر با
می‌خواهیم توپ‌های شکل مقابل را با رنگ‌های سبز، زرد و قرمز رنگ‌آمیزی کنیم ...
پاسخ: گزینه‌ی (د) (جواب=۱۲)
سه توپ زرد در این شکل باید همرنگ باشند. سه توپ قرمز هم همین‌طور. ابتدا رنگ سه توپ زرد را تعیین می‌کنیم (۳ حالت) و بعد رنگ سه توپ قرمز را تعیین می‌کنیم (۲ حالت) و بعد رنگ توپ سبز (۲ حالت) و بعد رنگ توپ آبی (۱ حالت). پس جواب طبق اصل ضرب میشه ۳*۲*۲ یعنی ۱۲
[center:06e4957a23]
دستگاهی داریم که یک جدول ۴ * ۴ را ...
پاسخ: سؤال غلط است!
به ازای هر جدول ورودی هرگز دستگاه چنین خروجی‌ای تولید نمی‌کند! (چرا؟)
[hr:06e4957a23]اول یه توضیح در مورد سؤالهای ۸ تا ۱۱ می‌نویسم.
ابتدا ببینیم کشور k+۱-منگولیا را چطور می‌تونیم بسازیم.
برای ساختن کشور k+۱-منگولیا کافیه دو تا k-منگولیا را کنار هم بگذاریم و شهرهای متناظر بین این دو کشور را به هم وصل کنیم.و در کشور اولی در ابتدای مبنای دوی شماره‌ی هرشهر یک صفر بنویسیم و در کشور دوم در ابتدای مبنای دوی شماره هر شهر رقم یک را بنویسیم.
[hr:06e4957a23]سؤال هشتم)
در کشور ۴-منگولیا ...
پاسخ: گزینه‌ی (الف) (جواب=۲)
اول شهرهای دو تا ۳-منگولیا را با دو رنگ همانطور که خواسته شده رنگ می‌کنیم و بعد به همون روشی که بالا گفتم دو تا از این‌ها را کنار هم می‌گذاریم و رنگ‌های یکی را معکوس می‌کنیم و شهرهای متناظر را به هم وصل می‌کنیم. پس رنگ‌آمیزی با دو رنگ ممکنه. حالا چطور اون ۳-منگولیاها رو رنگ کنیم؟ خب، دو تا ۲-منگولیا را رنگ می‌کنیم و کنار هم می‌گذاریم و ... (در واقع راه حل با استقرا بود)
[hr:06e4957a23]سؤال نهم)
حداقل با چند رنگ می‌توانیم به هریک از جاده‌های ...
پاسخ: گزینه‌ی (ج) (جواب=۷)
باز هم از استقرا استفاده می‌کنیم. جاده‌های دو تا ۶-منگولیا را با ۶ رنگ، رنگ می‌کنیم و وقتی شهرهای متناظر را به هم وصل کردیم، جاده‌های جدید را با رنگ هفتم، رنگ می‌کنیم. پس با ۷ رنگ ممکنه. از طرفی با ۶ رنگ و یا کمتر ممکن نیست. چون به هر شهر ۷ جاده وصله و این باعث میشه حداقل ۷ رنگ نیاز باشه.
[hr:06e4957a23]سؤال دهم)
در کشور ۱۰-منگولیا حداقل چند جاده را باید ...
پاسخ: گزینه‌ی (د) (جواب=
ابتدا دقت کنید که هر جاده دقیقاْ دو شهر را می‌بیند. پس تعداد جاده‌هایی که گل‌کاری می‌کنیم حداقل باید به اندازه‌ی نصف تعداد شهرها باشه. پس حداقل
[hr:06e4957a23]سؤال یازدهم)
در کشور ۱۱-منگولیا حداقل چند شهر را باید چراغانی کنیم ...
[JUSTIFY]پاسخ: گزینه‌ی (هـ) (جواب=
۱۱-منگولیا،
[hr:06e4957a23][/JUSTIFY]سؤال دوازدهم)
در یک سطر دل‌خواه حداکثر چند سکه ممکن است ...
پاسخ: گزینه‌ی (هـ) (جواب=۱۶)
کافی‌است در سطر اول ۱۶ سکه با عدد ۱ قرار دهیم.
[hr:06e4957a23]سؤال سیزدهم)
فرض کنید که تمام سکه‌های این جدول را برمی‌داریم و ...
پاسخ: گزینه‌ی (الف) (جواب=۱)
همه‌ی اعداد هر سطر متفاوتند. زیرا اگر عددی مثل ۳ دو بار در سطری بیاید، طبق شکل حداقل ۱۷ تا ۳ داریم، ولی نداریم!
[center:06e4957a23]
فرض کنید که جدول اولیه را مطابق شکل زیر ...
پاسخ: گزینه‌ی (د) (جواب=۷)
به شکل نگاه کنید. در سطر دوم ۷ تا عدد ۲ داریم.
[center:06e4957a23]
[hr:06e4957a23]سؤال پانزدهم)
علی ۳۱ کارت با شماره‌های ۱ تا ۳۱ دارد ...
پاسخ: گزینه‌ی (الف) (جواب=۳۰)
ابتدا دقت کنید که اعداد ۱ تا ۳۱ در مبنای دو، حداکثر ۵ رقمی هستند. پس XOR هر دو تا از آن‌ها هم حداکثر ۵ رقمی است و این یعنی بزرگترین XOR نمی‌تواند از ۳۱ بزرگتر باشد. پس گزینه‌ی (هـ) رد میشود. از طرفی ۳۱ هم ممکن نیست. چون اگر خروجی دستگاه ۳۱ باشد، در دو عدد ورودی، ارقام متناظر با هم متفاوتند (چرا؟). در این صورت مجموع این دو عدد، ۳۱ میشود (چرا؟) ولی مسئله گفته است که مجموع دو عدد ورودی باید ۳۲ باشد. حالا ببینیم چرا خروجی ۳۰ ممکن است. کافی است دو عدد ۱ و ۳۱ را به دستگاه بدهیم تا خروجی ۳۰ باشد.
[hr:06e4957a23]سؤال شانزدهم)
برنامه‌ی زیر چه عددی را چاپ خواهد کرد ...
پاسخ: گزینه‌ی (ج) (جواب=۱۳۹۰)
یگ نکته‌ی مهم در مورد XOR وجود دارد وآن نکته این است که ترتیب در XOR اهمیت ندارد. مثلاْ
اگر دقت کنید در این برنامه، در پایان خواهیم داشت:
[center:06e4957a23]
و طبق نکته‌ی بالا داریم:
[center:06e4957a23]
می‌دانیم XOR دو عدد مساوی صفر است و صفر نیز در XOR بی‌تأثیر است. پس :
[center:06e4957a23]
پاسخ: گزینه‌ی (ج) (جواب=۵۶۴)
خروجی برابر با
[hr:06e4957a23]سؤال هجدهم)
شش مکعب چند وضعیت شامل دقیقاْ ...
پاسخ: گزینه‌ی (ب) (جواب=۱۸۰۰ و ۱۲۰۰)
برای ساختن یک وضعیت با دو برج، کافی‌است یک جایگشت از اعداد ۱ تا ۶ بسازیم (!۶ حالت) و از یکی از ۵ جای ممکن آن را دو قسمت کنیم (۵ حالت). هر وضعیت را ۲ بار شمردیم پس تعداد وضعیت‌ها با دو برج برابر است با:
[center:06e4957a23]
[center:06e4957a23]
[hr:06e4957a23][JUSTIFY]سؤال نوزدهم)
یک «حرکت» شامل برداشتن بالاترین مکعب ...
پاسخ: گزینه‌ی (د) (جواب=۷ صعودی، ۷ نزولی)
این مسئله به توضیح زیادی نیاز ندارد. کافی است حرکت‌هایی که حتماْ باید انجام شوند را پیدا کنید و ...[/JUSTIFY][/center:06e4957a23]
[hr:06e4957a23]سؤال بیستم)
حداقل میزان K چقدر باید باشد که ...
پاسخ: گزینه‌ی (ب) (جواب=۱۰)
ابتدا دقت کنید که از هر وضعیتی با حداکثر ۱۰ حرکت می‌توان به هر وضعیت دیگر رسید. چون با حداکثر ۵ حرکت می‌توان همه‌ی برج‌ها را روی میز قرار داد و با حداکثر ۵ حرکت دیگر می‌توان هر حالت دیگر را ساخت. حال با مثالی نشان می‌دهیم که ۱۰ حرکت، حداقل تعداد حرکت مورد نیاز است. به شکل زیر نگاه کنید. برای تبدیل شکل سمت چپ به شکل سمت راست حداقل ۱۰ حرکت لازم است. پس جواب مسئله ۱۰ است.
[center:06e4957a23]
[hr:06e4957a23]سؤال بیست و یکم)
فرض کنید وضعیت راه‌های کشور طوری است که ...
پاسخ: گزینه‌ی (الف) (جواب=۲)
بدون شرح!
[center:06e4957a23]
فرض کنید مقصد مسیرهایی استقلالی است که ...
پاسخ: گزینه‌ی (ب) (جواب=۱۳۸۹)
از برهان خلف استفاده می‌کنیم. فرض کنید این کشور کمتر از ۱۳۸۹ شهر داشته باشد. حالا مسیری را در نظر بگیرید که از تعداد زیادی جاده خاکی تشکیل شده (جاده آسفالت ندارد). در این صورت بعد از عبور از ۱۳۸۸ امین جاده‌ی خاکی به شهری می‌رسیم که قبلاْ آن‌جا بوده‌ایم (چرا؟) و پرسپولیسی هم هست (چرا؟). در عبور از جاده خاکی بعدی به یک شهر استقلالی می‌رسیم و قبلاْ هم در آن نبوده‌ایم. ولی ممکن نیست که قبلاْ در این شهر استقلالی نبوده باشیم. چون گفتیم که در آن شهر پرسپولیسی قبلی، قبلاْ بوده‌ایم. پس بعد از آن حتماْ به این شهر استقلالی رفته‌ایم.
حالا باید یک مثال با ۱۳۸۹ شهر پیدا کنیم. کافی است شهرها را دور یک دایره بچینیم و به ترتیب با جاده خاکی به هم وصل کنیم. هر شهر هم با جاده آسفالت به خودش وصل میشود.
[hr:06e4957a23]سؤال بیست و سوم)
فرض کنید مقصد مسیر تنها و تنها وقتی ...
پاسخ: گزینه‌ی (ب) (جواب=۳۱)
فعلاْ حوصله‌ی اثباتش رو ندارم. فقط مثال را ببینید:
[center:06e4957a23]
ابتدا در یک سالن ۳*۳ ...
پاسخ: گزینه‌ی (هـ)
بدون شرح!
[center:06e4957a23]
فرایند سؤال قبل را در یک سالن ۴*۴ ...
پاسخ: گزینه‌ی (ب)
همه‌ی گزینه‌ها ۴ تا ۱ دارند ولی (ب) ۵ تا ۱ دارد.
[hr:06e4957a23]سؤال بیست و ششم)
فراین سؤال قبل را در یک سالن ۴*۴ ...
پاسخ: گزینه‌ی (الف)
بدون شرح!
البته راه ساده تر هم برای حل داره. ولی برای نوشتن این ساده ترین راهه :
[center:06e4957a23]
فرض می‌کنیم اگر دو عدد ورودی ...
پاسخ: گزینه‌ی (هـ)
نمی‌دونم چه‌طوری باید توضیح بدم. چون معلومه که این برنامه، عدد را در مبنای دو معکوس می‌کند.
[hr:06e4957a23]سؤال بیست و هشتم)
اگر ورودی برنامه مقدار X باشد ...
پاسخ: گزینه‌ی (هـ) (جواب = ۱۲۳)
۴۴۴ در مبنای ۲ میشود ۱۱۰۱۱۱۱۰۰ و طبق سؤال قبل خروجی برنامه در مبنای دو میشود ۱۱۱۱۰۱۱ که برابر با ۱۲۳ است.
[hr:06e4957a23]سؤال بیست‌ونهم)
عدد A را زیبا می‌نامیم اگر ...
پاسخ: گزینه‌ی (ج) (جواب=۹)
اعداد زیبا:
۱۰۱۱
۱۰۱۱۱
۱۰۰۱۱
۱۰۰۰۱۱
۱۰۰۱۱۱
۱۰۱۱۱۱
۱۰۱۰۱۱
۱۱۰۱۱۱
۱۰۰۱۰۱
[hr:06e4957a23]سؤال سیم)
چند تا از اعداد بین ...
پاسخ: گزینه‌ی (ب) (جواب=۹۹۲)
باید تعداد اعداد زیبای ۱۳ رقمی (در مبنای دو) را بشماریم.
محاسبه‌اش خیلی آسونه و توضیح راه حل در این‌جا طولانی میشه. پس فقط جواب رو ببینید:
[center:06e4957a23]
منبع: آقای محمدجواد نادری بنی
[/center:06e4957a23][/JUSTIFY]
