- ارسال ها
- 77
- لایک ها
- 124
- امتیاز
- 33
[h=1]چالش اندازه در فیزیک کوانتوم[/h]
تجربیات روزمره نشان میدهد اجسام بزرگ (همچون تخممرغ و انسان) به شکل برهمنهی از حالات٬ شبیه آنچه برای اشیاء کوانتومی (همچون الکترونها) رخ میدهد٬ ظاهر نمیشوند. آیا این به آن معنی است که فیزیک کوانتومی اساساً درمورد اجسام بزرگتر از یک حدّ خاص بکار نمیرود؟
به گزارش انجمن فیزیک ایران، آزمایش جدیدی با به دامانداختن حرکت یک اتم بزرگ در یک شبکهی اپتیکی این امکان را فراهم آورده تا بتوان نقطهی برشی برای این حدّ خاص تعیین کرد. با استفاده از این اسباب٬ کارستن روبیز (Carsten Robens) از دانشگاه بُن آلمان و همکارانش نشان دادهاند که یک اتم سزیم که در یک حالت غیرکلاسیکی مسیری را طی میکند٬ به عنوان یک برهمنهی از حالات حرکت کرده و بنابراین در یک زمان بیش از دو موقعیت مجزا را اشغال میکند. چنان ویژگیهای ذاتی کوانتومی از اشیاء بزرگ مشاهده شده است اما به نظر میرسد مشاهدات روبینز و همکارانش که برپایهی سختگیرانهترین آزمایش صورت گرفته٬ استانداردی طلایی برای تایید وجود برهمنهی باشد. به این ترتیب آزمایشی که آنها انجام دادهاند نظریاتی از فیزیک که در پی جایگزینی مکانیک کوانتومی هستند را محدود میسازد. از این فناوری میتوان به منظور آزمودن برهمنهی حتی در مقیاسهای بزرگ (همچون اتمها یا مولکولهای بزرگ) نیز بهره جست.
بسیاری از آزمایشهایی که قصد تایید برهمنهی کوانتومی را دارند به دنبال شاهدی بر تداخل هستند. آزمایش کلاسیک شامل عبور یک الکترون از یک جفت شکاف است: حلقههای نتیجهشده در این آزمایش رفتار موجمانندی را پیشنهاد میدهند که نظریه کوانتومی به ذرات بینیادی نسبت میدهد. با این حال حتی اگر این آزمایشها با آنچه مکانیک کوانتومی پیشبینی میکند سازگار باشد٬ آنها آزمونهای عاری از خط به حساب نمیآیند چون میتوان یک توضیح کلاسیک نیز بر این مطلب ارائه داد: میتوان تصور کرد که الکترون واقعاً از یکی از شکافها عبور میکند و هرگز به شکل همزمان از دو شکاف (آنطور که فیزیک کوانتومی به آن میپردازد) نمیگذرد.
در مقالهای نظری در سال ۱۹۸۵ آنتونی لگت (Anthony Leggett) و آنوپام گارگ (Anupam Garg) به این مسئله از نقطهنظر کاملاً متفاوتی نگریستند. آنها در صدد تایید مکانیک کوانتومی بر نیامدهاند بلکه پیشنهاد دادهاند که میتوان نشان داد هرچیزی بغیر از یک توصیف کوانتومی به تناقضی با مشاهدات تجربی منجر میشود. آنان نقطهنظری را موسوم به واقعگرایی بزرگمقیاس (ماکروریلیسم) تعریف کردهاند که بر مبنای دو فرض پایهگذاری شده و با مکانیک کوانتوم در تناقض است: یک جسم با اندازهی به حدُ کافی بزرگ همیشه در یک زمان در یک جا قرار دارد (برهمنهی ماکروسکوپیک نمیتواند وجود داشته باشد) و اینکه تعیین موقعیت این جسم بدون مختل ساختن آن امکانپذیر است. آنها نشان دادهاند که اگر این بینش صحیح باشد اندازهگیریهای انجام شده بر روی جسم در زمانهای مختلف میتواند به شکل آماری تنها تا درجهی معینی همبستگی از خود نشان میدهند؛ رابطهای که آنها به شکل ریاضی در نامساوی لگت-گارگ بیان داشتهاند. آزمایشهایی که این نامساوی را نقض میکنند به وضوح نشان میدهند که ماکروریلیسم صحیح نیست. کاری که آنها انجام دادهاند الهامبخش تعدادی آزمایش بر روی فوتونها٬ اسپین هستهای و مدارهای ابررسانا بوده است.
در مقایسه با این آزمایشها٬ اتمهایی که روبینز و همکارانش در آزمایشهای خود از آنها استفاده کردهاند بزرگترین اشیاء کوانتومی هستند که نامساوی لگت-گارگ در مورد آنها آزموده شده و در آنها از اندازهگیری موسوم به اندازهگیری تهی (null) بهره برده شده است. این اندازهگیری یک اندازهگیری «غیرتهاجمی» است که به نامساوی اجازه میدهد تا به متقاعدکنندهترین روش ممکن تایید شود. در آزمایشی که این پژوهشگران به انجام رساندهاند اتم سزیم در یکی از دو موج اپتیکی ایستاده حرکت میکند. این دو موج٬ از قطبش الکتریکی مخالف برخوردارند و مکان اتم در زمانهای مختلف اندازهگیری میشود. این دو موج ایستاده را میتوان به عنوان یک جفت کارتنهای یکبعدی شبیه کارتنهایی که تخممرغها را در آن نگه میدارند تصور کرد که باهمدیگر همپوشانی دارند (یکی به رنگ قرمز و دیگری به رنگ آبی – شکل زیر را ببینید).
در این آزمایش همبستگی مابین مکان اتم در زمانهای مختلف اندازهگیری میشود. روبینز و همکارانش ابتدا این اتم را در یک برهمنهی از حالات فوقریز اسپینی داخلی قرار دادهاند. این کار متناظر است با قرار داشتن در هر دو کارتن به شکل همزمان. سپس این دو موج اپتیکی را یکی پس از دیگری تضعیف کردهاند تا اتم سزیم در فاصلهای تا ۲ میکرومتر در حرکتی بنام پیمایش کوانتومی (quantum walk) گسترده گردد. سرانجام پژوهشگران این اتم را به لحاظ اپتیکی برانگیخته ساختهاند تا فلورسانس کند. عملی که موجب میشود موقعیت اتم در یک تک حالت آشکار شود. با دانستن آنکه اتم از کجا حرکت خود را آغاز میکند این امکان به پژوهشگران داده میشود تا به شکل متوسط تعیین کنند که اتم از نقطهی شروع خود به سمت راست حرکت میکند یا چپ. با تکرار این آزمایش آنان میتوانند همبستگی مابین مکان اتم را در زمانهای مختلف بدست آورده و در نامساوی لگت-گارگ قرار دهند.
اگر ماکروریلیسم واقعیت را توصیف کند٬ یک اندازهگیری تهی نتیجهی اندازهگیری فلورسانس نهایی را تحت تاثیر قرار میدهد و مقدار کل همبستگیِ مکان ذره در زمانهای مختلف بدون مکانیک کوانتومی قابل فهم و درک است. اما این موضوع با چیزی که در قلب مکانیک کوانتوم باعث شگفتآور شدن آن بوده رویارویی دارد. به طور قطع وقتی اتم گسترده میگردد (چنانکه موقعیت تعریفشدهای داشته باشد) حتی یک اندازهگیری تهی نیز اثری دارد. این گستردگی به یک همبستگی کلی قویتری نسبت به آنچه تحت ماکروریلیسم ممکن است میانجامد؛ حقیقتی که به شکل ریاضی بواسطهی نقض نامساوی لگت-گارگ حاصل میشود. این دقیقاً همان چیزی است که روبیز و همکارانش یافتهاند و این یعنی ماکروریلیسم را نمیتوان در مورد اتم سزیم بکار برد.
پس از تقریباً یک قرن از تحول کوانتومی در علم شاید شگفتآور باشد که فیزیکدانان هنوز در پی اثبات وجود برهمنهی هستند. انگیزهی اصلی در آیندهی فیزیک نظری نهفته است. ممکن است نظریات نوپای ماکروریلیسم بخوبی پایه و اساس نسل بعدی «ارتقاء»ی نظریه کوانتومی را (با تنظیم مقیاس برای مرزهای کوانتوم-کلاسیکی) تشکیل دهد. به یُمن نتایج حاصل از این آزمایشها میتوانیم مطمئن باشیم که این مرز نمیتواند زیر مقیاسی قرار بگیرد که اتم سزیم در آن مقیاسها همانند یک موج عمل میکند. این مقیاس چقدر بزرگ است؟ یک اندازهگیری نظری از بزرگمقیاسی٬ اتم سزیم را در رتبهی نسبتاً کم ۶٫۸ قرار میدهد که تنها اندکی بالاتر از دیگر اجسام آزمایششده با اندازهگیری تهی است اما بسیار پائینتر از مشکوکترین مرز جای میگیرد. (گربهی شرودینگر رتبهی ۵۷ را داراست).
در حقیقت آزمایشهای تداخلسنجی ماده-موج٬ پیشتر حلقههای تداخلی با مولکولهای فولرن باکمینستر (Buckminsterfullerene)٬ با رتبهبندی به بزرگی ۱۲ را به نمایش گذاشتهاند. با این حال به عقیدهی من میتوانیم نمایش مسلمتری از کوانتومی بودن اتم سزیم را بعلت عبور پژوهشگران این آزمایش از ماکروریلیسم بواسطهی اندازهگیریهای نتایج تهی داشته باشیم. گام بعدی٬ تلاش برای انجام آزمایشهایی با اتمهایی با جرم بیشتر است که در طول زمانهای بزرگتری برهمنهی کرده و با فواصل بیشتری از هم جدا شدهاند. این کار مرزهای بزرگمقیاس را هرچهبیشتر گسترده کرده و طبیعت رابطهی بین کوانتوم و جهان بزرگمقیاس را برملا میسازد. این پژوهش در مجلهی فیزیکال ریویو اکس انتشار یافته است.
سایت علمی بیگ بنگ /نویسنده خبر: زینالوند فرزین
تجربیات روزمره نشان میدهد اجسام بزرگ (همچون تخممرغ و انسان) به شکل برهمنهی از حالات٬ شبیه آنچه برای اشیاء کوانتومی (همچون الکترونها) رخ میدهد٬ ظاهر نمیشوند. آیا این به آن معنی است که فیزیک کوانتومی اساساً درمورد اجسام بزرگتر از یک حدّ خاص بکار نمیرود؟
به گزارش انجمن فیزیک ایران، آزمایش جدیدی با به دامانداختن حرکت یک اتم بزرگ در یک شبکهی اپتیکی این امکان را فراهم آورده تا بتوان نقطهی برشی برای این حدّ خاص تعیین کرد. با استفاده از این اسباب٬ کارستن روبیز (Carsten Robens) از دانشگاه بُن آلمان و همکارانش نشان دادهاند که یک اتم سزیم که در یک حالت غیرکلاسیکی مسیری را طی میکند٬ به عنوان یک برهمنهی از حالات حرکت کرده و بنابراین در یک زمان بیش از دو موقعیت مجزا را اشغال میکند. چنان ویژگیهای ذاتی کوانتومی از اشیاء بزرگ مشاهده شده است اما به نظر میرسد مشاهدات روبینز و همکارانش که برپایهی سختگیرانهترین آزمایش صورت گرفته٬ استانداردی طلایی برای تایید وجود برهمنهی باشد. به این ترتیب آزمایشی که آنها انجام دادهاند نظریاتی از فیزیک که در پی جایگزینی مکانیک کوانتومی هستند را محدود میسازد. از این فناوری میتوان به منظور آزمودن برهمنهی حتی در مقیاسهای بزرگ (همچون اتمها یا مولکولهای بزرگ) نیز بهره جست.
بسیاری از آزمایشهایی که قصد تایید برهمنهی کوانتومی را دارند به دنبال شاهدی بر تداخل هستند. آزمایش کلاسیک شامل عبور یک الکترون از یک جفت شکاف است: حلقههای نتیجهشده در این آزمایش رفتار موجمانندی را پیشنهاد میدهند که نظریه کوانتومی به ذرات بینیادی نسبت میدهد. با این حال حتی اگر این آزمایشها با آنچه مکانیک کوانتومی پیشبینی میکند سازگار باشد٬ آنها آزمونهای عاری از خط به حساب نمیآیند چون میتوان یک توضیح کلاسیک نیز بر این مطلب ارائه داد: میتوان تصور کرد که الکترون واقعاً از یکی از شکافها عبور میکند و هرگز به شکل همزمان از دو شکاف (آنطور که فیزیک کوانتومی به آن میپردازد) نمیگذرد.
در مقالهای نظری در سال ۱۹۸۵ آنتونی لگت (Anthony Leggett) و آنوپام گارگ (Anupam Garg) به این مسئله از نقطهنظر کاملاً متفاوتی نگریستند. آنها در صدد تایید مکانیک کوانتومی بر نیامدهاند بلکه پیشنهاد دادهاند که میتوان نشان داد هرچیزی بغیر از یک توصیف کوانتومی به تناقضی با مشاهدات تجربی منجر میشود. آنان نقطهنظری را موسوم به واقعگرایی بزرگمقیاس (ماکروریلیسم) تعریف کردهاند که بر مبنای دو فرض پایهگذاری شده و با مکانیک کوانتوم در تناقض است: یک جسم با اندازهی به حدُ کافی بزرگ همیشه در یک زمان در یک جا قرار دارد (برهمنهی ماکروسکوپیک نمیتواند وجود داشته باشد) و اینکه تعیین موقعیت این جسم بدون مختل ساختن آن امکانپذیر است. آنها نشان دادهاند که اگر این بینش صحیح باشد اندازهگیریهای انجام شده بر روی جسم در زمانهای مختلف میتواند به شکل آماری تنها تا درجهی معینی همبستگی از خود نشان میدهند؛ رابطهای که آنها به شکل ریاضی در نامساوی لگت-گارگ بیان داشتهاند. آزمایشهایی که این نامساوی را نقض میکنند به وضوح نشان میدهند که ماکروریلیسم صحیح نیست. کاری که آنها انجام دادهاند الهامبخش تعدادی آزمایش بر روی فوتونها٬ اسپین هستهای و مدارهای ابررسانا بوده است.
در مقایسه با این آزمایشها٬ اتمهایی که روبینز و همکارانش در آزمایشهای خود از آنها استفاده کردهاند بزرگترین اشیاء کوانتومی هستند که نامساوی لگت-گارگ در مورد آنها آزموده شده و در آنها از اندازهگیری موسوم به اندازهگیری تهی (null) بهره برده شده است. این اندازهگیری یک اندازهگیری «غیرتهاجمی» است که به نامساوی اجازه میدهد تا به متقاعدکنندهترین روش ممکن تایید شود. در آزمایشی که این پژوهشگران به انجام رساندهاند اتم سزیم در یکی از دو موج اپتیکی ایستاده حرکت میکند. این دو موج٬ از قطبش الکتریکی مخالف برخوردارند و مکان اتم در زمانهای مختلف اندازهگیری میشود. این دو موج ایستاده را میتوان به عنوان یک جفت کارتنهای یکبعدی شبیه کارتنهایی که تخممرغها را در آن نگه میدارند تصور کرد که باهمدیگر همپوشانی دارند (یکی به رنگ قرمز و دیگری به رنگ آبی – شکل زیر را ببینید).
در این آزمایش همبستگی مابین مکان اتم در زمانهای مختلف اندازهگیری میشود. روبینز و همکارانش ابتدا این اتم را در یک برهمنهی از حالات فوقریز اسپینی داخلی قرار دادهاند. این کار متناظر است با قرار داشتن در هر دو کارتن به شکل همزمان. سپس این دو موج اپتیکی را یکی پس از دیگری تضعیف کردهاند تا اتم سزیم در فاصلهای تا ۲ میکرومتر در حرکتی بنام پیمایش کوانتومی (quantum walk) گسترده گردد. سرانجام پژوهشگران این اتم را به لحاظ اپتیکی برانگیخته ساختهاند تا فلورسانس کند. عملی که موجب میشود موقعیت اتم در یک تک حالت آشکار شود. با دانستن آنکه اتم از کجا حرکت خود را آغاز میکند این امکان به پژوهشگران داده میشود تا به شکل متوسط تعیین کنند که اتم از نقطهی شروع خود به سمت راست حرکت میکند یا چپ. با تکرار این آزمایش آنان میتوانند همبستگی مابین مکان اتم را در زمانهای مختلف بدست آورده و در نامساوی لگت-گارگ قرار دهند.

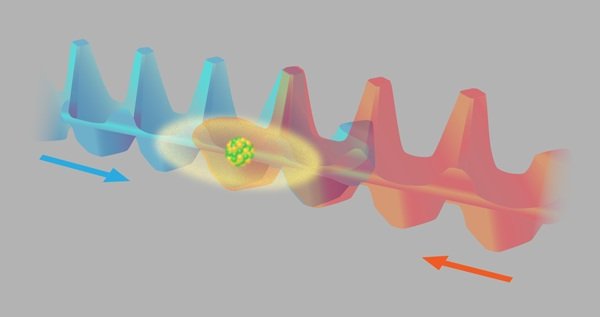
در آزمایشی که توسط روبینز و همکارانش انجام شده٬ یک اتم بزرگ (سزیم) در یکی از دو میدان اپتیکی ممکن حرکت میکند (که به رنگ قرمز و آبی نشان داده شده است). این میدانها پتانسیل متناوبی شبیه «کارتن تخممرغ» دارد. این پژوهشگران اتم سزیم را در برهمنهی از دو حالت اتمی مهیا کردهاند که معادل است با قرار گرفتن همزمان اتم در کارتن اپتیکی آبی و قرمز رنگ. آنها موقعیت اتم را با آشکارسازی فلورسانس آن هنگامی که دو کارتن از هم جدا میشوند تعیین کردهاند.
اکنون یک ماکروریلیست تایید میکند که این اتم هرگز نمیتواند از یک حالت برهمنهی حرکت خود را آغاز کند٬ در عوض در هر لحظه تنها در صندوقچهای شامل یکی از کارتنها قرار دارد. علاوه بر آن وی بر این باور است که اندازهگیری فلورسانس نسبت به اندازهگیری بعدی٬ حالت تهاجمی خواهد داشت. بنابراین همانگونه که لگت و گارگ ابتداعاً فرض کردهاند٬ روبیز و همکارانش از فناوری اندازهگیری «نتیجهی تهی» در یکی از زمانهای میانی آزمایششان استفاده کردهاند. به بیان ساده یک اندازهگیری تهی آزمایشگر را قادر میسازد تا بدون اندرکنش با اتم٬ موقعیت آن را تعیین کند. به این منظور پژوهشگران یکی از امواج ایستاده (یا کارتنها) را با فاصلهی زیادی جابجا کردهاند. در نظر میگیریم که کارتنِ به رنگ قرمز را جابجا کردهاند. اگر چنانچه اتم پس از یک اندازهگیریِ فلورسانس٬ از خود نور نتابد میتوان فهمید که اتم در کارتن قرمز قرار داشته٬ با آن بشدت اندرکنش کرده و نهایتاً در فاصلهی دورتری از آن به حرکت خود پایان میدهد. با این وجود با تکرار این آزمایش بعضی مواقع میتوان تابیدن نور از اتم را دید. میتوان دریافت که اتم قبل از این جابجاشدن در کارتن آبی بوده است. بعلاوه کارتن آبی (و بنابراین اتم سزیم) با آن مداخلهای نداشته است.اگر ماکروریلیسم واقعیت را توصیف کند٬ یک اندازهگیری تهی نتیجهی اندازهگیری فلورسانس نهایی را تحت تاثیر قرار میدهد و مقدار کل همبستگیِ مکان ذره در زمانهای مختلف بدون مکانیک کوانتومی قابل فهم و درک است. اما این موضوع با چیزی که در قلب مکانیک کوانتوم باعث شگفتآور شدن آن بوده رویارویی دارد. به طور قطع وقتی اتم گسترده میگردد (چنانکه موقعیت تعریفشدهای داشته باشد) حتی یک اندازهگیری تهی نیز اثری دارد. این گستردگی به یک همبستگی کلی قویتری نسبت به آنچه تحت ماکروریلیسم ممکن است میانجامد؛ حقیقتی که به شکل ریاضی بواسطهی نقض نامساوی لگت-گارگ حاصل میشود. این دقیقاً همان چیزی است که روبیز و همکارانش یافتهاند و این یعنی ماکروریلیسم را نمیتوان در مورد اتم سزیم بکار برد.
پس از تقریباً یک قرن از تحول کوانتومی در علم شاید شگفتآور باشد که فیزیکدانان هنوز در پی اثبات وجود برهمنهی هستند. انگیزهی اصلی در آیندهی فیزیک نظری نهفته است. ممکن است نظریات نوپای ماکروریلیسم بخوبی پایه و اساس نسل بعدی «ارتقاء»ی نظریه کوانتومی را (با تنظیم مقیاس برای مرزهای کوانتوم-کلاسیکی) تشکیل دهد. به یُمن نتایج حاصل از این آزمایشها میتوانیم مطمئن باشیم که این مرز نمیتواند زیر مقیاسی قرار بگیرد که اتم سزیم در آن مقیاسها همانند یک موج عمل میکند. این مقیاس چقدر بزرگ است؟ یک اندازهگیری نظری از بزرگمقیاسی٬ اتم سزیم را در رتبهی نسبتاً کم ۶٫۸ قرار میدهد که تنها اندکی بالاتر از دیگر اجسام آزمایششده با اندازهگیری تهی است اما بسیار پائینتر از مشکوکترین مرز جای میگیرد. (گربهی شرودینگر رتبهی ۵۷ را داراست).
در حقیقت آزمایشهای تداخلسنجی ماده-موج٬ پیشتر حلقههای تداخلی با مولکولهای فولرن باکمینستر (Buckminsterfullerene)٬ با رتبهبندی به بزرگی ۱۲ را به نمایش گذاشتهاند. با این حال به عقیدهی من میتوانیم نمایش مسلمتری از کوانتومی بودن اتم سزیم را بعلت عبور پژوهشگران این آزمایش از ماکروریلیسم بواسطهی اندازهگیریهای نتایج تهی داشته باشیم. گام بعدی٬ تلاش برای انجام آزمایشهایی با اتمهایی با جرم بیشتر است که در طول زمانهای بزرگتری برهمنهی کرده و با فواصل بیشتری از هم جدا شدهاند. این کار مرزهای بزرگمقیاس را هرچهبیشتر گسترده کرده و طبیعت رابطهی بین کوانتوم و جهان بزرگمقیاس را برملا میسازد. این پژوهش در مجلهی فیزیکال ریویو اکس انتشار یافته است.
سایت علمی بیگ بنگ /نویسنده خبر: زینالوند فرزین
