یه نوعی از تابع
پاسخ : یه نوعی از تابع
اگه زحمتی نیست بخشای ریاضی رو اینجا تایپ کنید بعد عکسشو تو بخشی که میخواین بنویسین کپی کنین که مشکلی واسه خوندنشون پیش نیاد: Online LaTeX Equation Editor - create, integrate and download ممنون
از آنجایی که جبرای ایران یه حالی هستن و کلا با جبرای دنیا ساز مخالف میزنن برآن شدیم جبری بزاریم که سخت نیست ولی یه حالیه
Fn(xاز دو متغیره x,nداده شده متغیره xهمه ی اعداد حقیقی ومتغیره nاعداد طبیعی را اختیار میکند.
F[SUB]1(x)=cos x[/SUB] , F[SUB]n+1(x)+F(x+1)=Fn(x[/SUB]
تابع با این خاصییت را معین کنید
Fn(xاز دو متغیره x,nداده شده متغیره xهمه ی اعداد حقیقی ومتغیره nاعداد طبیعی را اختیار میکند.
F[SUB]1(x)=cos x[/SUB] , F[SUB]n+1(x)+F(x+1)=Fn(x[/SUB]
تابع با این خاصییت را معین کنید
پاسخ : یه نوعی از تابع
بله دیگه آخه اون چیزی که استاد نوشتن برای2/(
= \lef\fr{} \right )e^{x}\left ( 1-e \right )+e^{-x}\left ( 1-1/e \right )) ) =
) =
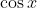
که حالا برای هر nای خود این e یافتن میخواد آخه توی مسائل تابعی باید صورت تابعی که میدیم به عنوان تابع نهایی باید پارامتر جدیدی نداشته باشه که توی یه تابع خاص که قرارش میدیم خود این پارامتر هم یافتن بخواد مثلا اگه f=axبشه با ازای همه ی f هاست وa هرعددی باشه okیه باید تابع به صورت سینوس کسینوسی باشه اشتباه میکنم؟
بله دیگه آخه اون چیزی که استاد نوشتن برای2/(
که حالا برای هر nای خود این e یافتن میخواد آخه توی مسائل تابعی باید صورت تابعی که میدیم به عنوان تابع نهایی باید پارامتر جدیدی نداشته باشه که توی یه تابع خاص که قرارش میدیم خود این پارامتر هم یافتن بخواد مثلا اگه f=axبشه با ازای همه ی f هاست وa هرعددی باشه okیه باید تابع به صورت سینوس کسینوسی باشه اشتباه میکنم؟
آخرین ویرایش توسط مدیر
پاسخ : یه نوعی از تابع
جوابی که نوشته بودم درست بود ، فقط یک ضریب i تو توان داشت که فراموش کرده بودم . عبارتی هم که استاد Shoki براتون بدست اورده ، که نسبت به باقیمونده به ۴ حالت بندی کرده در واقع به خاطر مرتبه ۴ بودن عدد i هست .
چیزی که گودرز نوشته دقیقا بسط همونیه که من نوشتم ، شاید با اون راحت تر باشی :5:!
جوابی که نوشته بودم درست بود ، فقط یک ضریب i تو توان داشت که فراموش کرده بودم . عبارتی هم که استاد Shoki براتون بدست اورده ، که نسبت به باقیمونده به ۴ حالت بندی کرده در واقع به خاطر مرتبه ۴ بودن عدد i هست .
چیزی که گودرز نوشته دقیقا بسط همونیه که من نوشتم ، شاید با اون راحت تر باشی :5:!
آخرین ویرایش توسط مدیر
