یک سوال زیبا از هندسه(حتما روش فکر کنید)
پاسخ : یک سوال زیبا از هندسه(حتما روش فکر کنید)
حل:
محل تقاطع دایره محاطی با
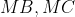رو
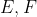بنامید.به راحتی بدست میاد:
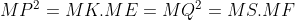
از طرفی حکم مساله معادله با:
که با استفاده از قضیه سینوس ها در دایره محاطی به این شکل ساده میشه:
که با توجه به رابطه هایی که اول گفتم نتیجه میشه:
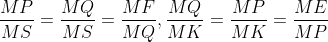
در نتیجه حکم مساله معادله با:
از طرفی اگر محل تقاطع bc با دایره محاطی رو L بنامیم با دو تا تشابه بدست میاد:
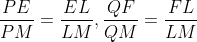
حال با تقسیم دو طرف رابطه آخری که معادل با حکم مساله هست، بر mp بدست میاد:
که بطلمیوس در چهارضلعی mfle هست.حالا چون روابط بالا برگشت پذیرند حکم مساله درسته
سوالی که الان ذهن من رو درگیر کرده اینه که آیا راه حل کوتاه تری هم وجود داره؟!:225:
حل:
محل تقاطع دایره محاطی با
از طرفی حکم مساله معادله با:
که با استفاده از قضیه سینوس ها در دایره محاطی به این شکل ساده میشه:
که با توجه به رابطه هایی که اول گفتم نتیجه میشه:
در نتیجه حکم مساله معادله با:
از طرفی اگر محل تقاطع bc با دایره محاطی رو L بنامیم با دو تا تشابه بدست میاد:
حال با تقسیم دو طرف رابطه آخری که معادل با حکم مساله هست، بر mp بدست میاد:
که بطلمیوس در چهارضلعی mfle هست.حالا چون روابط بالا برگشت پذیرند حکم مساله درسته
سوالی که الان ذهن من رو درگیر کرده اینه که آیا راه حل کوتاه تری هم وجود داره؟!:225:
- ارسال ها
- 331
- لایک ها
- 264
- امتیاز
- 0
پاسخ : یک سوال زیبا از هندسه(حتما روش فکر کنید)
قرار بود دنبال روش غير محاسباتي برويم...
حل:
محل تقاطع دایره محاطی با
رو
بنامید.به راحتی بدست میاد:
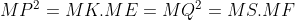
از طرفی حکم مساله معادله با:
که با استفاده از قضیه سینوس ها در دایره محاطی به این شکل ساده میشه:
که با توجه به رابطه هایی که اول گفتم نتیجه میشه:
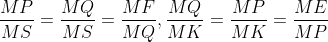
در نتیجه حکم مساله معادله با:
از طرفی اگر محل تقاطع bc با دایره محاطی رو L بنامیم با دو تا تشابه بدست میاد:
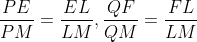
حال با تقسیم دو طرف رابطه آخری که معادل با حکم مساله هست، بر mp بدست میاد:
که بطلمیوس در چهارضلعی mfle هست.حالا چون روابط بالا برگشت پذیرند حکم مساله درسته
سوالی که الان ذهن من رو درگیر کرده اینه که آیا راه حل کوتاه تری هم وجود داره؟!:225:
محل تقاطع دایره محاطی با
از طرفی حکم مساله معادله با:
که با استفاده از قضیه سینوس ها در دایره محاطی به این شکل ساده میشه:
که با توجه به رابطه هایی که اول گفتم نتیجه میشه:
در نتیجه حکم مساله معادله با:
از طرفی اگر محل تقاطع bc با دایره محاطی رو L بنامیم با دو تا تشابه بدست میاد:
حال با تقسیم دو طرف رابطه آخری که معادل با حکم مساله هست، بر mp بدست میاد:
که بطلمیوس در چهارضلعی mfle هست.حالا چون روابط بالا برگشت پذیرند حکم مساله درسته
سوالی که الان ذهن من رو درگیر کرده اینه که آیا راه حل کوتاه تری هم وجود داره؟!:225:
پاسخ : یک سوال زیبا از هندسه(حتما روش فکر کنید)
از m موازی pq یه خط رسم کنین و دو تا تالس بنویسید، محاسبات خیلی کوتاه میشه...
.
تعمیم: در مثلث abc یه بیضی داریم که در p,q,r بر ab,ac,bc مماسه. پاره خط واصل راس a به مرکز بیضی، بیضی رو تو m قطع میکنه. mb, mc پاره خط pq رو در s,t قطع میکنه. ثابت کنید st نصف pq ه.
از m موازی pq یه خط رسم کنین و دو تا تالس بنویسید، محاسبات خیلی کوتاه میشه...
.
تعمیم: در مثلث abc یه بیضی داریم که در p,q,r بر ab,ac,bc مماسه. پاره خط واصل راس a به مرکز بیضی، بیضی رو تو m قطع میکنه. mb, mc پاره خط pq رو در s,t قطع میکنه. ثابت کنید st نصف pq ه.
پاسخ : یک سوال زیبا از هندسه(حتما روش فکر کنید)
درسته که این راه حل محاسباتیه،ولی محاسباتش کلا دو تا شاه کلید و یه قضیه سینوس هاست.بقیش همش با تشابه و قوت و زاویه بازیه
مثلا خط اول این جوری نتیجه میشه که چون
پس mp بر دایره محیطی مثلث pkf مماسه و به همین شکل برای mq.
یا این قسمت"
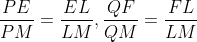" یه لم هست که با استفاده از تشابه یا زیر میانه میشه بدستش اورد.
کلا باید ks رو به pq ربط بدیم که احتمالا یا محاسباتیه یا باید خط اضافه کنیم.
درسته که این راه حل محاسباتیه،ولی محاسباتش کلا دو تا شاه کلید و یه قضیه سینوس هاست.بقیش همش با تشابه و قوت و زاویه بازیه
مثلا خط اول این جوری نتیجه میشه که چون
یا این قسمت"
از طرفی اگر محل تقاطع bc با دایره محاطی رو L بنامیم با دو تا تشابه بدست میاد:
کلا باید ks رو به pq ربط بدیم که احتمالا یا محاسباتیه یا باید خط اضافه کنیم.