☻ماراتن سوالات ریاضی دوم دبیرستان☺

Ali Akbar Kabiri · 1391/4/6

پاسخ : سوال 10

جان......!!!!!!!:13::13::13::13:
اینا دیگه چی اند؟؟؟؟!!!! leq چیه؟؟؟
این سوال برای اول دبیرستانه ها....

msaeids · 1391/4/6

پاسخ : سوال 10

msaeids · 1391/4/6

پاسخ : ماراتن سوالات ریاضی اول دبیرستان

دوباره مشکل پیش اومد تو تایپ ریاضی من عذر میخوام
دو رابطه ی اول رو میدانیم و رابطهی سوم از جمع آندو حاص میشود
درفایل زیر روابط موجودند
http://latex.codecogs.com/gif.downl...2&space;یعنی&space;در&space;بازه&space;[-2و2]

mehran88 · 1391/4/6

پاسخ : سوال 10

فیزیکخوان گفت

این سوال و سوال قبلی اصلا و ابدا ربطی به مباحث کتابی اول دبیرستان ندارند و جزو مباحث کتابای درسی سوم دبیرستان هستند.حالا اگه شما علاقمند هستید بحث دیگه ای داره.ولی دلیل نمیشه جزو مباحث اول دبیرستان مطرحشون کنید.:23:

رادیکال 2 +رادیکال 3 گنگه؟؟؟

اثبات:اول از همه ثابت می کنیم که رادیکال 2 یا رادیکال 3 گنگه.

حالا خلف میزنیم و فرض می کنیم رادیکال 2 +رادیکال 3 گویا باشه.مثلا رادیکال 2 رو میبریم اون طرف و طرفین رو به توان 2 میرسونیم.

به تناقض میرسیم.

-------------------------------------------------------------------------

$R_{sinx+cosx}=?$

طبق نامساوی کوشی داریم.

$(ad+bc)^2\leq (a^2+b^2)(c^2+d^2)$

پس:

$(sinx+cosx)^2\leq 2(sin^2x+cos^2x)\Leftrightarrow -\sqrt{2}\leq sinx+cosx\leq \sqrt{2}$

mehran88 · 1391/4/6

پاسخ : ماراتن سوالات ریاضی اول دبیرستان

msaeids گفت

این کارتون اشتباهه.

واسه بدست آوردن برد یک تابع وقتی میاییم از چند تا نامساوی استفاده می کنیم بازه ای بدست میاریم که برد تابع زیر مجموعه ای از این بازه هستش و لزوما با اون برابر نیست.

طبق کار شما یعنی x ای یافت میشود که حاصل عبارت

$sinx+cosx$

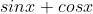2 شود.یعنی باید هم cosx و هم sin x یک شود.یعنی مثلا

$x=\frac{\pi }{2}$

و

$x=0$

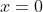.آیا X می تونه همزمان دو مقدار متفاوت داشته باشه؟؟؟ نه.

یکی از روش های درست رو اینجا نوشتم.

http://www.irysc.com/forum/t8772-post112995/#post112995

برای کپی کردن فرمول ها از لاتکس هم روی عکس فرمول نوشته شده راست کلیک کنید و عکس رو کپی کنید.حالا فقط توی اینجا پیستش کنید و دوباره لینک اینا ندید:1:

Wizard · 1391/4/6

پاسخ : سوال 10

به نام خداوند دانا و توانا

سلام بر همگی

من فکر می کنم این را باید از طریق مثلثات سال دوم حل کرد.

مسلما ما مقدار x را نمی دانیم اما می توانیم بگوییم که از چه حدی بالاتر و از چه حدی پایین تر نمی شود.

برای این کار باید از مفهوم تابع مطلع(( وابستگی یک یا چند متغیر به یک متغیر خاص))

می دانیم که صورت توابع خطی y=ax+b یا f(x)=ax+b می باشد. خوب این فقط یک مثال بود همین

در ریاضی ما به بازه ای که می توانیم در y قرار بدیم می گوییم برد. به بازه ای که می توانیم در x قرار دهیم دامنه می گوییم

در ریاضی توابع مثلثاتی نیز داریم که تابع سینوسی آن به صورت زیر است

f(x)=asinbx +c

در تابع کسینوسی ، به صورت زیر است
(a ضریبی است که در نسبت مثلثاتی ضرب شده اما b ضریبی است که در درجه که x است ضرب شده و c عرض از مبدا است))

f(x)=a.cosb.x+c

در ریاضی برای بدست آوردن کمترین و بیشترین مقدار برد در تابع سینوسی یا کسینوسی (هر دو) از یک قانون استفاده می کنیم

بیشترین
B|+C= f(x)[SUB]max[/SUB]|

کمترین
B|+C= f(x)min|-

حالا این کار را برای حل این مساله می کنیم

اولا sinx+cosx را یک تابع در نظر می گیریم

یعنی

f(x)=sinx+cosx

حالا با استفاده از فرمول بیشترین حد برد (B|+C= f(x)[SUB]max[/SUB]|) این کار را می کنیم

f(x)[SUB]max[/SUB]=1+cosx

حالا بیشترین حالت cosx را در یک تابع دیگر در نظر می گیریم

f'(x)[SUB]max[/SUB]=1

در فرمول قبلی جای گذاری کنید

f(x)[SUB]max[/SUB]=1+1=2

اما کمترین حد

f(x)=-|1|+cosx

حالا کمترین مقدار cosx را در یک تابع جداگانه بررسی می کنیم

f'(x)[SUB]min[/SUB]=-|1|=-1

حالا کمترین حالت cosx را در بجای cosx در فرمول قبلی می گذاریم

f(x)[SUB]min[/SUB]=-|1|-1=-2

یادآوری شود که f(x) همان y می باشد.

حالا که کمترین و بیشترین مقدار f(x) را داریم آن را در یک بازه می نویسیم

[-2,2]

این بازه جواب این مساله هست

من جواب را نمی دانستم ولی وقتی جواب گفته شد طبق مطالعاتی که کردم به ذهنم آمد که باید این کار را کرد

با تشکر

msaeids · 1391/4/6

پاسخ : ماراتن سوالات ریاضی اول دبیرستان

اصلا جوابای دوتا سوال آخر رو رو کاغذ نوشتم اسکن کردم
خلاصا
ینم لینکش
http://img4up.com/up2/95687719061108732990.jpg
فقط برعکسه :دی

mehran88 · 1391/4/6

پاسخ : سوال 10

محلط12 گفت

سلام

متاسفانه جوابتون درست نیست.

شما در واقع کار دوست قبلی مون رو کردید که دلیل اشتباه بودنش رو پایین توضیح دادم

ماراتن سوالات ریاضی اول دبیرستان - صفحه 7

msaeids · 1391/4/6

پاسخ : سوال 10

mehran88 گفت

این سوال و سوال قبلی اصلا و ابدا ربطی به مباحث کتابی اول دبیرستان ندارند و جزو مباحث کتابای درسی سوم دبیرستان هستند.حالا اگه شما علاقمند هستید بحث دیگه ای داره.ولی دلیل نمیشه جزو مباحث اول دبیرستان مطرحشون کنید.:23:

رادیکال 2 +رادیکال 3 گنگه؟؟؟

اثبات:اول از همه ثابت می کنیم که رادیکال 2 یا رادیکال 3 گنگه.

حالا خلف میزنیم و فرض می کنیم رادیکال 2 +رادیکال 3 گویا باشه.مثلا رادیکال 2 رو میبریم اون طرف و طرفین رو به توان 2 میرسونیم.

به تناقض میرسیم.

-------------------------------------------------------------------------

$R_{sinx+cosx}=?$

طبق نامساوی کوشی داریم.

$(ad+bc)^2\leq (a^2+b^2)(c^2+d^2)$

پس:

$(sinx+cosx)^2\leq 2(sin^2x+cos^2x)\Leftrightarrow -\sqrt{2}\leq sinx+cosx\leq \sqrt{2}$

بله شما درست میگید متوجه شدم

threehandsnal · 1391/4/6

پاسخ : سوال 10

فیزیکخوان گفت

از این اتحاد میشه استفاده کرد(البته تو سال سوم میخونیدش! ولی گفتم بدونین بد نباشه)

تو این فرمول

$\arctan\left ( \frac{b}{a} \right )$

هم یعنی مقدار زاویه ای در بازه -180 تا 180 که تانژانت اون زاویه بشه b/a !

که با این فرمول مساله خورده میشه :3:

اثباتش هم اینجاست:
http://www.sinclair.edu/centers/mat...orksheets/215,216/ConvertingTheForm_asinx.pdf

graph · 1391/4/6

پاسخ : سوال 10

فیزیکخوان گفت

$\sin (x) + \cos (x) = \sqrt{2}(\frac{\sqrt(2)}{2} \sin (x) + \frac{\sqrt(2)}{2} \cos (x)) = \sqrt(2) \sin(x + \frac{\Pi}{4}) \Rightarrow R = [-\sqrt(2), \sqrt(2)]$

orion · 1391/4/6

پاسخ : سوال 10

threehandsnal گفت

البته اون که تو سال سوم هست این نیست!!!!!بچه های سوم خواب اینو هم نمیبینن
اون که تو سومه حالت خاصa=b=1 هست

ali_irysc · 1391/4/6

پاسخ : ماراتن سوالات ریاضی اول دبیرستان

الان یه چیزی یادم اومد که کتاب های ریاضی دبیرستان برای سال های قبل که تغییر نکرده بود خیلی بهتر از این کتاب ها بود
مثلا برای 8 سال پیش رو نیگاه کنید میبینید خیلی بهتره هم از نظر علمی هم از هر نظر
اون موقع همه این نسبت های مثلثاتی معادله سهمی و... خیلی از چیزای دیگه که از کتاب مثلا سال اول برداشتن بود
الان کتاب ریاضی شده کتاب قصه انگاری کتاب برای افراد مهد کودکه همش بچه بازی شده
الان شده کاربردی
به خدا اگه بری این کتاب ها رو بخونی خیلی بیشتر لذت ریاضی رو میبری تا این کتاب هایی که الان دستته

من از وقتی که سال اول بودم تا الان که پیش هستم همه این کتاب ها رو سال به سال تغییر دادن ولی من شانس اوردم اینا رو برادرم داشت از همون اول هم حالم از این کارشون به هم خورد ( اوحححققق)
فردا که شما تو این مملکت یه کاره ای میشی ( و ما زیر دستت ) یه فکری به حال این کتاب های مضخرفی که الان اومده و نظام نمره ای و کنکور قلمچی گاج و..تست و دکترا های بیسواد یا الکی یا مدرک های پولی و... بکنی
که وضع خیلی خرابه دادا
در قرن های پیش یه کتاب بود ولی کتاب بود ولی الان تو کتاب قروشی ها رو نیگاه کنی هزار تا کتاب هست ولی هیچکدومش به درد بخور نیست فقط انواع و اقسام به رنگ های مختلف
هر کدومتون این کتاب ها به دستتون رسید امید وارم لذتشو ببرید برای من که خیلی لذت بخش بود حداقل یه خاطره خوبی که از دبیرستانم دارم اینه که اینا رو خوندم
اگه لینک دانلود این کتاب ها رو پیدا کردم حتما همین جا ان شا الله میزارم

Ali Akbar Kabiri · 1391/4/7

پاسخ : سوال 10

mehran88 گفت

دوست عزیز این سوال در کتاب مبتکران سال اول دبیرستان مطرح شده است.
هم چنین در مدارس خاص ( مثلا سمپاد ) تدریس می شود.

در ضمن جوابتون هم درسته ، تبریک....!

SMASZOP · 1391/4/7

پاسخ : ماراتن سوالات ریاضی اول دبیرستان

میدونیم رادیکال 6 عددی گنگ است(قابل اثبات) فرض میکنیم رادیکال 2 بعلاوه ی رادیکال 3 گویاست پس:

که این خلافه فرض است چون رادیکال 6 که گنگ است برابر عدد گویا شده پس رادیکال 2 بعلاوه رادیکال 3 گنگ است!

Ali Akbar Kabiri · 1391/4/7

پاسخ : ماراتن سوالات ریاضی اول دبیرستان

SMASZOP گفت

تبریک....!
پاسخ شما کوتاه ترین و بهترین پاسخ بود.
ممنون

graph · 1391/4/7

پاسخ : ماراتن سوالات ریاضی اول دبیرستان

مجموعه جواب های این معادله را پیدا کنید

$n! + 3 = {3}^{n-1}$

threehandsnal · 1391/4/7

پاسخ : ماراتن سوالات ریاضی اول دبیرستان

graph گفت

واضحه که معادله برای n های نامثبت جواب نداره.حالا n=1 رو بررسی می کنیم و میبینیم که جواب نیست.
برای n>1 میدونیم طرف راست بر 3 بخش پذیره پس سمت چپ هم باید باشه.واضجه که n=2 جواب نیست.حالا برای n>2 داریم:

$n!=3(3^{n-2}-1)$

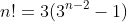که نشون میده که !n بر 3 بخشپذیره ولی بر 9 و توانهای بزرگتر 3 بخشپذیر نیست.از طرف دیگه

$\forall n_{\geq 6}:9|n!$

که این نتیجه میده که

$3\leq n\leq 5$

که با عدد گذاری می بینیم که معادله

$\boxed{n=3}\:\:,\:\:\boxed{n=4}$

رو داره.

-maedeh-love · 1392/7/9

پاسخ : ماراتن سوالات ریاضی اول دبیرستان

میشه ثابت کنید رادیکال 6 گنگ است؟
و اینکه اگر p عدد اول باشد،رادیکال p گنگ است؟

Mostafa_ · 1392/7/10

پاسخ : ماراتن سوالات ریاضی اول دبیرستان

-maedeh-love گفت

این سوال اول دبیرستان نیست ... برای جبر سومه ... کلا برای اینکه ثابت کنید عدد رادیکال x گنگه اینکارارو بکنید:

1- برهان خلف بزنید و فرض کنید گویا باشه

2- با توجه به تعریف عدد گویا (a و b عضو Z و b مخالف صفر و نسبت به هم اولند ... یعنی ب.م.م. این دو عدد یکه) به این برسید که دو عدد نسبت به هم اول نیستند و این تناقضه ... برای اینکار هم طرفین رو به توان فرجه رادیکال برسونید و طرفین وسطین کنید .... مثلا به این میرسید : a^n=x.b^n ... خوب واضحه که چون a^n مضرب x هست خود a هم مضرب x ـه .... مثلا a=x.k ... حالا اینو تو معادله اصلی قرار بدید و می بینید که به تناقض اینکه دو عدد اول نیستند میرسید

☻ماراتن سوالات ریاضی دوم دبیرستان☺

Moderator

New Member

New Member

New Member

New Member

Moderator

New Member

New Member

New Member

New Member

New Member

Well-Known Member

New Member

Moderator

مشاور فیزیک

Moderator

New Member

New Member

New Member

New Member