AE=EF=FA ===> S(ABE) +S(ADE) =S(EFC) i

[mahanmath]

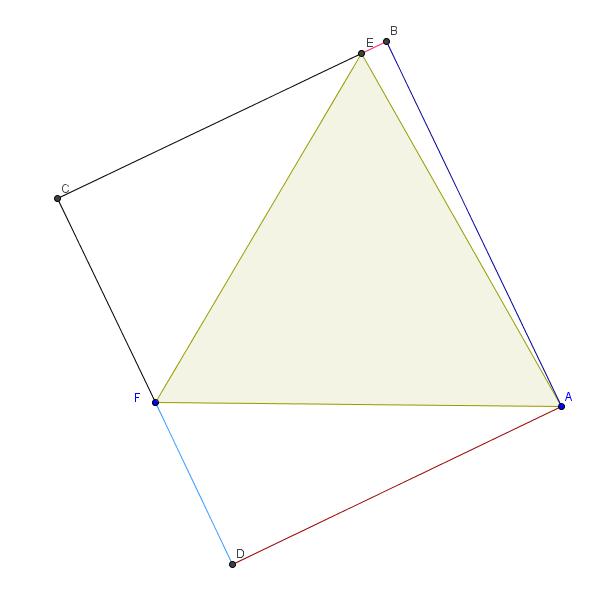
ABCD یه مستطیل هست ، اون مثلثی هم که داخلش قرار داره متساوی ال اضلاع هست :


۱)ثابت کنید مجموع مساحت‌های ۲ مثلث ABE ، ADF برابر مساحت مثلث EFC است .
۲)شرط لازم و کافی‌ وجود نقاطی با شرایط E,F را روی اضلاع مستطیل ABCD بیابید .
۳)با فرض وجود این نقاط ، آن هارا با خط کش و پرگار پیدا کنید .

PS : قسمت ۱ این سوال رو math-sina بهم داد . قسمت‌های ۲،۳ رو خودم اضافه کردم ، به نظرم از مساله اصلی‌ جذاب ترن :205: !

 

[Aref]

پاسخ : AE=EF=FA ===> S(ABE) +S(ADE) =S(EFC) i

۲)شرط لازم و کافی‌ وجود نقاطی با شرایط e,f را روی اضلاع مستطیل abcd بیابید .

شرط لازم و کافیش اینه که bc از رادیکال سه تقسیم بر دو ab کمتر نباشد.فکر کنم.

 

[mahanmath]

پاسخ : AE=EF=FA ===> S(ABE) +S(ADE) =S(EFC) i

درسته ! در واقع باید اینطوری بگیم :87::

\frac{\sqrt 3}{2}\le\frac{AD}{AB}\le\frac{2}{\sqrt 3}
حال داشتی بنویس اثباتشو

 

[math]

پاسخ : AE=EF=FA ===> S(ABE) +S(ADE) =S(EFC) i

میشه لطفا بگید سوال در سطح چه سوادیه؟

 

[fereidoon]

پاسخ : AE=EF=FA ===> S(ABE) +S(ADE) =S(EFC) i

وقتي توي هندسه ي مقدماتي نوشته شده،يعني سطحش به مرحله دو نميرسه.

 

[mahanmath]

پاسخ : AE=EF=FA ===> S(ABE) +S(ADE) =S(EFC) i

قسمت (۳) در حد خیلی‌ مقدماتی هست (۴ ضلعی محاطی !) ، قسمت‌های (۱)،(۲) هم در حد کتاب درسی‌ سوم دبیرستان هستند , منظورم اینه که برای حلشون باید کمی‌ مثلثات بلد باشید . البته قسمت (۱) راه بدون مثلثات هم داره .

 

[math]

پاسخ : AE=EF=FA ===> S(ABE) +S(ADE) =S(EFC) i

یک سوال اثبات قسمت دوم رو میشه بذارید؟

 

[mahanmath]

پاسخ : AE=EF=FA ===> S(ABE) +S(ADE) =S(EFC) i

قرار بدید

، بعد نسبت طول به عرض مستطیل می‌شه یه چیزی تو مایه‌های :

بعد هم چون

همون نتیجه که بالا عارف گفت بدست میاد .

 

[Aref]

پاسخ : AE=EF=FA ===> S(ABE) +S(ADE) =S(EFC) i

قرار بدید

، بعد نسبت طول به عرض مستطیل می‌شه یه چیزی تو مایه‌های :

بعد هم چون

همون نتیجه که بالا عارف گفت بدست میاد .

اصلا راحت تر هم میشه:
یه مثلث متساوی الاضلاع روی خط ae و رو به داخل مستطیل بسازید و e رو از b تا c تکون بدید و از قضیه ی مقدار میانی استفاده کنید.

 

[mahanmath]

پاسخ : AE=EF=FA ===> S(ABE) +S(ADE) =S(EFC) i

اصلا راحت تر هم میشه:
.........

چرا حس میکنی‌ این راحت تره :217: ؟ از نظر ریاضی‌ هم فکر می‌کنم اثباتی که گفتم rigour تره ، چون به هر حال به پیوستگی اون تابع که روش مقدار میانی زدی می‌شه گیر داد :98:!

 

[math]

پاسخ : AE=EF=FA ===> S(ABE) +S(ADE) =S(EFC) i

سوال 1 با دکارت هم حل میشه (البته فکر کن) معادلهی خط های CE,CF AE,AF رو که بنویسیم با استفاده از مثلثات به عبارت زیر می رسیم

که ادامش بدیهی است.

 

[math-sina]

پاسخ : AE=EF=FA ===> S(ABE) +S(ADE) =S(EFC) i

من راه حل این سوالو خیلی ساده مینویسم :
اول میام پاره خط ها رو نام گذاری میکنم:

میخوایم ثابت کنیم :

برای این کار هم میایم. مثلث های AEB و ADF رو از اون ضلع برابرشون بهم میچسبونیم. (یعنی نقطه ی F رو میزاریم رو نقطه ی E) و مساحت چهار ضلعی حاصل رو از دو راه حساب میکنیم. از طرفی قطر AE رو رسم میکنیم. دو برابر مساحت میشه :

حالا قطر BD رو رسم میکنیم. دو برابر مساحت میشه :

که همون چیزیه که میخواستیم