f(x)f(y)<=|x-y
- ارسال ها
- 48
- لایک ها
- 173
- امتیاز
- 0
پاسخ : f(x)f(y)<=|x-y
اینجا به 2 روش حل شده که یکیش ماله منه :4:
AoPS Forum - Functional Equations Marathon • Art of Problem Solving
اینجا به 2 روش حل شده که یکیش ماله منه :4:
AoPS Forum - Functional Equations Marathon • Art of Problem Solving
پاسخ : f(x)f(y)<=|x-y
راه حلت فوق العادست!!!!!!:192::118:
یه راه دیگه میتونه ایدش این باشه :
اول به جای تابع
با تابع
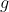کار کنید که
=\sqrt{2g(x)})
، در این صورت فرض مساله معادل می‌شه با
+g(y)&space;\right&space;)^2&space;-&space;\left&space;(g(x)-g(y)&space;\right&space;)^2&space;=4g(x)g(y)&space;\leq&space;(x-y)^2)
تعبیر هندسی این نامساوی اینه که اگه
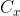دایره به مرکز
))
و مماس به محور x باشه ، اون موقع برای
&space;\in&space;\mathbb{Q}&space;\times&space;\mathbb{Q}^c)
داریم
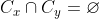
اما ناشمارا دایره جدا از هم نمی‌شه توی صفحه رسم کرد (چرا ؟)
اول به جای تابع
اما ناشمارا دایره جدا از هم نمی‌شه توی صفحه رسم کرد (چرا ؟)