بعضی از دوستان از من خواسته بودند که مطلبی رو در مورد SMV بذارم ...
به خاطر همین سعی می کنم که SMV رو معرفی کنم و بعدش طرز استفاده از اون که مهم تر از اثباتش هست رو بیان کنم. اثبات قضیه رو ، که در واقع اثبات یک لم خواهد بود، ان شاء الله در فرصتی دیگر خواهم گفت.
[center:52cea469af][HIGHLIGHT=#ffffff]The stronger mixing variables method - S.M.V[/HIGHLIGHT]
از یک تعریف شروع می کنیم :
فرض کنید که
 دنباله ای دلخواه از اعداد حقیقی باشد. تبدیل
دنباله ای دلخواه از اعداد حقیقی باشد. تبدیل
 را مطابق زیر تعریف می کنیم:
را مطابق زیر تعریف می کنیم:
1- اندیس های
 را طوری انتخاب می کنیم که:
را طوری انتخاب می کنیم که:


با استفاده از فرض مسئله به دست می آوریم:


اما سوالی که ممکن است پیش آید آن است که ما چگونه پی بردیم که آن عبارت بر
 بخش پذیر است. دلیل این موضوع ساده است. اگر دقت کنید نامساوی اصلی دو حالت تساوی بدیهی دارد یعنی
بخش پذیر است. دلیل این موضوع ساده است. اگر دقت کنید نامساوی اصلی دو حالت تساوی بدیهی دارد یعنی
 و
و
 . حال باتوجه به این حالات اگر مقادیر
. حال باتوجه به این حالات اگر مقادیر
 ،
،
 یا
یا
 باشد پس نامساوی باید به تساوی تبدیل شود یعنی دو تا از ریشه های چند جمله ای
باشد پس نامساوی باید به تساوی تبدیل شود یعنی دو تا از ریشه های چند جمله ای
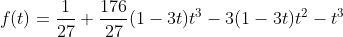 همین مقادیر خواهند بود. بدین ترتیب چند جمله ای بر
همین مقادیر خواهند بود. بدین ترتیب چند جمله ای بر
 . حال چند جمله ای را بر این عبارات تقسیم می کنیم تا چند جمله ای درجه ی دومی بدست آید. در ادامه باید دوباره ریشه های آن چند جمله ای را پیدا کرد و ...
. حال چند جمله ای را بر این عبارات تقسیم می کنیم تا چند جمله ای درجه ی دومی بدست آید. در ادامه باید دوباره ریشه های آن چند جمله ای را پیدا کرد و ...
برای فهمیدن تجزیه عبارتی که بعد از انجام S.M.V به وجود می آید، همین استدلال را می توان در حل سوالات دیگر به کار برد. از طرفی دقت کنید که برای حل مسائلی که در آن ها حالت تساوی می تواند به گونه ای باشد که تمامی متغیر ها با هم برابر نباشند، بهتر است همانند بالا چند متغیر اول (از لحاظ بزرگی) یا چند متغیر آخر(از لحاظ بزرگی) را انتخاب کرد به گونه ای که در همه ی حالات تساوی آن متغیر ها با هم برابر باشند (همان طور که برای سوال پیش برای متغیرهای
 این طور بوده است و در هر دو حالت تساوی آن سه با هم برابر بوده اند). البته دقت کنید که ممکن است در کل یک حالت تساوی داشته باشیم که آن هم زمانی اتفاق بیفتد که همه ی متغیر ها در آن مساوی اند اما باز هم لازم باشد همانند بالا عمل کنیم.
این طور بوده است و در هر دو حالت تساوی آن سه با هم برابر بوده اند). البته دقت کنید که ممکن است در کل یک حالت تساوی داشته باشیم که آن هم زمانی اتفاق بیفتد که همه ی متغیر ها در آن مساوی اند اما باز هم لازم باشد همانند بالا عمل کنیم.
حال سراغ یک نامساوی دیگر می رویم اما راه حل کامل آن ذکر نخواهد شد...
مسئله ی 3. اگر
 و
و
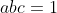 ثابت کنید:
ثابت کنید:
[center:52cea469af]

*مسئله ی 9. اگر
 و
و
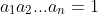 و
و
 ثابت کنید:
ثابت کنید:
[center:52cea469af]

(این مسئله احتیاج به مشتق گیری دارد)[/center:52cea469af]
_______________________________________________________________________________________________
در مورد مشتق در اینجا یک توضیح (کاملا) غیر دقیق و مختصری رو می دهم:
فرض کنید که
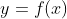 آن تابع باشد. مشتق آن را با
آن تابع باشد. مشتق آن را با
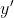 یا
یا
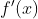 نشان می دهیم.
نشان می دهیم.
ابتدا به سراغ چند قاعده ی مشتق گیری می رویم...
در موارد زیر
 و اعداد ثابتی می باشند و
و اعداد ثابتی می باشند و
 نیز توابعی بر حسب
نیز توابعی بر حسب
 می باشند. قواعد مشتق گیری:
می باشند. قواعد مشتق گیری:









در حالت بالا اگر x صحیح باشد مشتق نداریم.

حال به سراغ توابع مثلثاتی می رویم:



در حالت بالا می توانید از این نکته استفاده کنید که
 و سپس از طریق قاعده ی 7 ام، مشتق آن را بگیرید.
و سپس از طریق قاعده ی 7 ام، مشتق آن را بگیرید.
دیگه این توابعی بود که فکر کنم مهم ترین ها بودند. اگر همین قدر رو بلد باشین به راحتی می تونید ینسن رو یاد بگیرید.
هر گاه در حل مسائل نامساوی به تابعی برخوردید و می خواستید که حداقل یا حداکثر آن را بیابید، اگر خواستید از طریق مشتق بروید، باید از آن تابع مشتق بگیرید!! اما قبل از آن باید دو سر بازه را چک کنید. یعنی ببینید که اگر x برابر دو سر بازه باشد مقدار آن تابع چه خواهد بود. سپس مشتق بگیرید.
بعد از این که از اون تابع مشتق گرفتید آن را مساوی صفر قرار می دهید یعنی:
 . این معادله یک سری جواب به شما می دهد یعنی
. این معادله یک سری جواب به شما می دهد یعنی
 . حال تمامی این n مقدار را در
. حال تمامی این n مقدار را در
 قرار می دهیم. یعنی
قرار می دهیم. یعنی
 را محاسبه می کنیم. از بین این مقادیر حداقل و حداکثر را می یابیم. در آن صورت آن مقادیر حداقل و حداکثر
را محاسبه می کنیم. از بین این مقادیر حداقل و حداکثر را می یابیم. در آن صورت آن مقادیر حداقل و حداکثر
 خواهند بود.
خواهند بود.
در واقع با کمی دقت متوجه این موضوع می شوید که قضیه ی لاگرانژ تعمیم همین موضوعه...
امیدوارم از لحاظ مشتق گیری مشکلاتتون کمتر شده باشه
 ...
...
هر گونه اشکالی در متن رو فورا بهم بگید تا اصلاح بشه. یک خواهش دیگه این که کسایی که انگلیسیشون در حدی نیست که مطالب فرنگی (!) رو بخونن حتما سعی کنند که این مشکل رو برطرف کنند... یاد گرفتن انگلیسی ریاضوی تنها به یاد گرفتن چند اصطلاح تخصصی احتیاج داره ... همین و بس !
با تشکر.
shoki

به خاطر همین سعی می کنم که SMV رو معرفی کنم و بعدش طرز استفاده از اون که مهم تر از اثباتش هست رو بیان کنم. اثبات قضیه رو ، که در واقع اثبات یک لم خواهد بود، ان شاء الله در فرصتی دیگر خواهم گفت.
[center:52cea469af][HIGHLIGHT=#ffffff]The stronger mixing variables method - S.M.V[/HIGHLIGHT]
The stronger mixing variables - S.M.V theorem
در این قسمت به معرفی قضیه ی S.M.V می پردازیم.از یک تعریف شروع می کنیم :
فرض کنید که
1- اندیس های
2- مقادیر
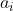 و
و
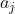 را با
را با
 عوض کنید.
عوض کنید.
در ادامه به یک لم اشاره می کنیم:
(همان طور که گفتم از نوشتن اثبات این لم صرف نظر می کنم، اما به این نکته توجه کنید که اثبات قضیه ی بعدی همان اثبات لم بالا می باشد)
حال قضیه ی S.M.V را بیان می کنیم:
اگر
 تابعی پیوسته، متقارن و کران دار از پایین باشد به گونه ای که
تابعی پیوسته، متقارن و کران دار از پایین باشد به گونه ای که
[center:52cea469af]

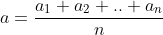
 می تواند متفاوت باشد و هر گونه تیدیلی که حالت میانگین داشته باشد می توان به جای آن قرار بگیرد که پرکاربردترین آن ها عبارتند از:
می تواند متفاوت باشد و هر گونه تیدیلی که حالت میانگین داشته باشد می توان به جای آن قرار بگیرد که پرکاربردترین آن ها عبارتند از:
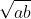 ،
،
 . که بسته به فرض(های) سوال، باید تبدیل مناسب را انتخاب کرد.
. که بسته به فرض(های) سوال، باید تبدیل مناسب را انتخاب کرد.
در ادامه به یک لم اشاره می کنیم:
لم- (General mixing variables lemma) فرض کنید که روی دنباله ی
 تبدیل
تبدیل
 را بی نهایت بار انجام داده باشیم. در آن صورت هر یک از
را بی نهایت بار انجام داده باشیم. در آن صورت هر یک از
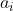 ها به مقدار زیر میل می کنند:
ها به مقدار زیر میل می کنند:
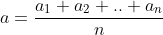 [/center:52cea469af]
[/center:52cea469af]
(همان طور که گفتم از نوشتن اثبات این لم صرف نظر می کنم، اما به این نکته توجه کنید که اثبات قضیه ی بعدی همان اثبات لم بالا می باشد)
حال قضیه ی S.M.V را بیان می کنیم:
اگر
[center:52cea469af]
که در آن
 دنباله ای از اعداد حقیقی است که با تبدیل
دنباله ای از اعداد حقیقی است که با تبدیل
 از دنباله ی
از دنباله ی
 به دست آمده باشد. در آن صورت داریم:
به دست آمده باشد. در آن صورت داریم:
 [/center:52cea469af]
[/center:52cea469af]
که در آن
که در آن
[center:52cea469af]
با استفاده از این قضیه، هر وقت خواستیم نامساوی ای رو اثبات کنیم، کافیست که بزرگترین و کوچکترین اعداد را انتخاب کنیم و سپس عملیات مورد نیاز را انجام دهیم!
[/center:52cea469af]با توجه به اثبات لم بیان شده در بالا، خواهید دید که تبدیل
S.M.V theorem and some applications
در این قسمت به طرز استفاده از قضیه ی S.M.V در حل مسائل خواهیم پرداخت.
بیش ترین کاربرد قضیه ی S.M.V در حل نامساوی های چهار متغیره است. اکثر نامساوی های چهار متغیره به وسیله ی این قضیه خیلی راحت تر حل می شوند.
در ابتدا از حل نامساوی حسابی-هندسی شروع می کنیم.
مسئله ی 1. اگر
 ثابت کنید:
ثابت کنید:
[center:52cea469af]
 [/center:52cea469af][center:52cea469af]
[/center:52cea469af][center:52cea469af]
حال برای افتتاحیه واقعی، از حل یک مسئله ی معروف shortlist شروع می کنیم!
مسئله ی 2. فرض کنید
 و
و
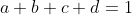 . ثابت کنید:
. ثابت کنید:
[center:52cea469af]

بیش ترین کاربرد قضیه ی S.M.V در حل نامساوی های چهار متغیره است. اکثر نامساوی های چهار متغیره به وسیله ی این قضیه خیلی راحت تر حل می شوند.
در ابتدا از حل نامساوی حسابی-هندسی شروع می کنیم.
مسئله ی 1. اگر
[center:52cea469af]
بدون از دست دادن کلیت مسئله فرض کنید
 . حال تعریف کنید:
. حال تعریف کنید:


باید ثابت کنیم:

که این معادل است با:
[/center:52cea469af]
که درست می باشد. پس داریم:
[center:52cea469af]

و بدیهیست که
 . پس حکم ثابت می شود.
. پس حکم ثابت می شود.

[/center:52cea469af]
حال برای افتتاحیه واقعی، از حل یک مسئله ی معروف shortlist شروع می کنیم!
مسئله ی 2. فرض کنید
[center:52cea469af]
راه حل. سعی کنید که تک تک مراحل این راه حل را به خوبی یاد بگیرید چون در ادامه همین مراحل برای حل مسائلی دیگر استفاده خواهد شد. بدون از دست دادن کلیت مسئله فرض کنید
 . تعریف کنید:
. تعریف کنید:
 [/center:52cea469af]
[/center:52cea469af]
[center:52cea469af]
با استفاده از فرض مسئله به دست می آوریم:
بنابراین،
[/center:52cea469af]
[center:52cea469af]
دلیل آخرین نتیجه گیری آن است که:

اگر و فقط اگر،

و این همان چیزیست که اثبات کردیم.
حال اگر تبدیل
 را بی نهایت بار روی
را بی نهایت بار روی
 انجام دهیم بدست می آوریم:
انجام دهیم بدست می آوریم:


حال اگر تبدیل
و داریم
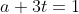 . پس نامساوی با جایگذاری
. پس نامساوی با جایگذاری
 به نامساوی زیر تبدیل می شود:
به نامساوی زیر تبدیل می شود:
که با یک تجزیه تبدیل می شود به:
 [/center:52cea469af]
[/center:52cea469af]
که بدیهیست چرا که
 . پس مسئله اثبات می شود.
. پس مسئله اثبات می شود.

اما سوالی که ممکن است پیش آید آن است که ما چگونه پی بردیم که آن عبارت بر
برای فهمیدن تجزیه عبارتی که بعد از انجام S.M.V به وجود می آید، همین استدلال را می توان در حل سوالات دیگر به کار برد. از طرفی دقت کنید که برای حل مسائلی که در آن ها حالت تساوی می تواند به گونه ای باشد که تمامی متغیر ها با هم برابر نباشند، بهتر است همانند بالا چند متغیر اول (از لحاظ بزرگی) یا چند متغیر آخر(از لحاظ بزرگی) را انتخاب کرد به گونه ای که در همه ی حالات تساوی آن متغیر ها با هم برابر باشند (همان طور که برای سوال پیش برای متغیرهای
حال سراغ یک نامساوی دیگر می رویم اما راه حل کامل آن ذکر نخواهد شد...
مسئله ی 3. اگر
[center:52cea469af]
راهنمایی: از تبدیل
 استفاده کنید.دقت کنید که به هیچ وجه نمی توانید از تبدیل
استفاده کنید.دقت کنید که به هیچ وجه نمی توانید از تبدیل
 استفاده کنید (چرا؟).
استفاده کنید (چرا؟).
حال سعی کنید که این نامساوی ها را با همین روش حل کنید.
مسئله ی 4. اگر
 به طوری که
به طوری که
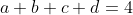 ثابت کنید:
ثابت کنید:

مسئله ی 5. اگر
 و
و
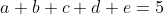 ثابت کنید:
ثابت کنید:

حال سعی کنید که این نامساوی ها را با همین روش حل کنید.
مسئله ی 4. اگر
مسئله ی 5. اگر
مسئله ی 6. اگر
 و
و
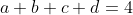 ثابت کنید:
ثابت کنید:

مسئله ی 7. اگر
 و
و
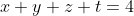 ثابت کنید:
ثابت کنید:

مسئله ی 8. اگر
 ثابت کنید:
ثابت کنید:
 [/center:52cea469af]
[/center:52cea469af]
*مسئله ی 9. اگر
[center:52cea469af]
(این مسئله احتیاج به مشتق گیری دارد)
منبع:
The stronger mixing variables method , Pham Kim Hung , Mathematical Reflections 6, 2006
در مورد مشتق در اینجا یک توضیح (کاملا) غیر دقیق و مختصری رو می دهم:
فرض کنید که
ابتدا به سراغ چند قاعده ی مشتق گیری می رویم...
در موارد زیر
در حالت بالا می توانید از این نکته استفاده کنید که
دیگه این توابعی بود که فکر کنم مهم ترین ها بودند. اگر همین قدر رو بلد باشین به راحتی می تونید ینسن رو یاد بگیرید.
هر گاه در حل مسائل نامساوی به تابعی برخوردید و می خواستید که حداقل یا حداکثر آن را بیابید، اگر خواستید از طریق مشتق بروید، باید از آن تابع مشتق بگیرید!! اما قبل از آن باید دو سر بازه را چک کنید. یعنی ببینید که اگر x برابر دو سر بازه باشد مقدار آن تابع چه خواهد بود. سپس مشتق بگیرید.
بعد از این که از اون تابع مشتق گرفتید آن را مساوی صفر قرار می دهید یعنی:
در واقع با کمی دقت متوجه این موضوع می شوید که قضیه ی لاگرانژ تعمیم همین موضوعه...
امیدوارم از لحاظ مشتق گیری مشکلاتتون کمتر شده باشه

هر گونه اشکالی در متن رو فورا بهم بگید تا اصلاح بشه. یک خواهش دیگه این که کسایی که انگلیسیشون در حدی نیست که مطالب فرنگی (!) رو بخونن حتما سعی کنند که این مشکل رو برطرف کنند... یاد گرفتن انگلیسی ریاضوی تنها به یاد گرفتن چند اصطلاح تخصصی احتیاج داره ... همین و بس !
با تشکر.
shoki

