x/(xy+1)+y/(yz+1)+z/(zx+1)>=3/2
M_Sharifi گفت
داریم
[center:133bf517fa]
 [/center:133bf517fa]از طرفی
[/center:133bf517fa]از طرفی
[center:133bf517fa]
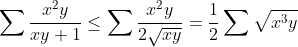
[center:133bf517fa]
[center:133bf517fa]
بنابراین کافی است ثابت کنیم
 و یا به صورت معادل،
و یا به صورت معادل،
 . این نابرابری نیز همان نابرابری قوی و معروف
. این نابرابری نیز همان نابرابری قوی و معروف

است که البته اثباتش چندان راحت نیست.
[/center:133bf517fa]
Man be namosavie akhar residam va khodam ro koshtam

Vasile hast
ke halat tasavi haye ajib gharibi dare va az hame badtar in ke man ino dide boodamo yadam rafte



kheily mamnoon.











