بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

[fisa ghores]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

آقا یکی جواب سوال 6 رو بإاره !لزومی نداره درست باشششششششششه:219:

 

[ehsan-mokhtarian]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

برای سوال 6 ثابت می کنیم ماکزیمم دو جمله ی متوالی بعد از چند حرکت کم می شه.
برهان خلف میزنیم.
دو تا جمله متوالی بگیرین.قبول داربن که اگه بزرگتر از 3 باشن عدد بعدی که تولید می شه کوچکتر مساوی ماکزیمم دو جمله هست.اگه کوچکتر بود که حالت بندی می کنیم و تو عددای بعدی دو تا عدد کوچکتر از اون ماکزیمم پیدا می شه.
اگه مساوی بود هم که بعد از 1 یا 2 مرحله عدد 4 به وجود می یاد.بعد از عدد 4 هم عددی که تولید می شه از عدد قبلی 4 کمتره.در هر دو صورت هم از فرض خلف هم استفاده کردم.پس حالا یه زیر دنباله ی نامتناهی از اعداد طبیعی داریم که اکیدا نزولیه.و این تناقضه.من تو 4 صفحه نوشتمش.حالت بندیاش خیلی زیاد می شه.

فکر کنم این راه درست باشه (من هم همین جوری حل کردم ) البته می شد بهتر هم بیانش کرد مثلا دنباله (b(n رو ماکسیمم 2 جمله ی متوالی می گیری و اثبات می کنی نزولیه (البته تا وقتی که به 4 برسه) بعد هم با 3 حالت به راحتی سوال حل می شه

 

[ash1374]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

ایده های من برای سوالات امروز:
مقدمه: چون حل سوالات امروز کمی طولانیه ممکنه یکم گنگ باشه. هر سوالی واضح نبود تا آخر امشب بگید، سعی می کنم حل کاملش را بنویسم

4. PT رو امتداد بدید تا دایره ی دیگر رو برای بار دوم در S قطع کنه. ثابت کنید ASبا PK موازیه. بعد نتیجه بگیرید AT میانه ی وارد بر PK در مثلث PAK هست و بعدش با میانخط توی مثلث PP'K و یه زاویه بازی ساده، حکم رو نتیجه بگیرید.

5. این یکم سخته نوشتنش اینجا. عدد خانه ی سطر i ام و ستون j ام رو با

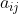نشون میدیم. اول ثابت کنید اگر یک جدول 3 در 3 رو بشه صفر کرد اونوقت

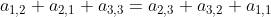. اثبات این قسمت زیاد سخت نیس. فقط به مکان این خونه ها و عملیات های مجاز توجه کنید. بعد ثابت کنید برعکسش هم درسته. یعنی اگه تو یه جدول سه در سه رابطه ی بالا برقرار بود حتما میشه صفرش کرد. برای اثبات این قسمت اول جدول 3 در 3 ای که وسطش یکه و بقیه صفره رو دستی صفر کنید. این که این جدول رو میشه صفر کرد یعنی اگر همین عملیات رو روی یه جدول 3 در 3 دیگه پیاده کنیم، خونه ی وسطش یک واحد کم میشه و بقیه دست نمی خورن. و به این ترتیب خونه ی وسط هر 3 در 3 رو میشه صفر کرد و بقیه دست نمی خورن. بعد که خونه ی وسط صفر شد، بدون این که حرکتی انجام بدین که خونه ی وسط خراب بشه، 6 تا خونه ای که تو رابطه ی بالا هستن رو صفر کنید. آخرش هم خونه های گوشه ی راست بالا و چپ پایین رو صفر کنید.
تا حالا نتیجه شد جدول 3 در 3 صفر میشه اگر و فقط اگر اون رابطه برقرار باشه. حالا روی m+n استقرا بزنید... بقیش سادس از اون رابطه باید نتیجه بگیریم اگر یه سطر یا ستون اضافه به یه جدول صفر اونوقت بجز خونه ی گوشش بقیش همش باید عدد های مساوی توش باشه و ...
حالت 2درn هم به عهده ی خواننده می گذاریم. (همینطور حالت 1 در n رو:4

3. اول ثابت کنید دنباله کران داره. فرض کنید بزرگترین عضوش n باشه. حالا دو تایی a,b کلا n[SUP]2[/SUP] حالت داره. پس طبق لانه کبوتری یه دو تایی مثلث a,b هست که تو دنباله دو بار اومدن. یعنی مثلا دنباله این شکلیه :

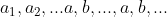حالا چون با دو عضو همه ی اعضای بعدی بدست میان پس دنباله متناوبه. یعنی اون چیزایی که بعد از a,b اولی میاد، بعد از a,b دومی هم دقیقا تکرار میشه. حالا لم زیر رو ثابت کنید و حکم رو به سادگی(البته نسبتاً به سادگی:4 نتیجه بگیرید:
لم: اگر a,b,c طبیعی باشند و a>3 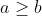و

و

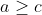باشد آنگاه :

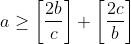
واقعا امروز آزمون سختی بود. خسته نباشید...

 

[سلندر]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

من 5 را حل کردم فقط برای حالت n*2 نوشتم چون زیر جدول 3*3 معنی نداره بررسی نمیکنیم چقدر کم میشه؟؟

 

[Alireza_h76]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

اقا من اولي ام و فكر ميكنم كه ١٢ نمره اي بگيرم به نظرتون خوبه؟

 

[MNikdan]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

من خودم که قبول نمیشم...
ولی دو تا از دوستام سوم هستن و یکیشون 22 و یکیشون 24 میشه(البته نمره ها رو حدودی گفتم)
به نظرتون قبول میشن ؟؟؟

 

[MNikdan]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

اقا من اولي ام و فكر ميكنم كه ١٢ نمره اي بگيرم به نظرتون خوبه؟

من هم نمره م بین 12 و 15 میشه. ولی چون سال اولم راضی ام.

 

[ali.bsh]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

من خودم که قبول نمیشم...
ولی دو تا از دوستام سوم هستن و یکیشون 22 و یکیشون 24 میشه(البته نمره ها رو حدودی گفتم)
به نظرتون قبول میشن ؟؟؟

اتفاقا ما هم یه اولی داریم از 3 تا یه 7-8 تا جواب داد.

 

[hamidreza hashempour]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

کاملا موافقم این همه حرص میخورید تا روز نتایج
فرض کنید اصلا امتحان ندادید

 

[sadra75]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

این سوالارو نمیشه با استقرا اثبات کرد(اگه کسی هم با استقرا اثبات کرده باشه احتمالا این جوری حل کرده که به فرض استقرا 1 ترازو سنگین تر اضافه کنه و... که کاملا غلطه)
من تو کف سوال 3ام کسی تونسته کاریش بکنه؟ اصلا نمی فهمم چجوری باید از خاصیت نقطه ی n استفاده کرد.

 

[Aref]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

راستی کف پارسال 19 بود نه 18...
امتحان امسال استاندارد بود کف هم باید حدود 23- 25 باشه (البته احتمالا ) و زیاد هم به گفته ی دیگران توجه نکنید و کار خودتون رو بکنید
راستی هرکی هر سوالی رو گفته حل کرده لزومی نداره 7 بگیره برای مثال یه تعداد زیادی برای سوال 5 حالت 2*n رو جدا بررسی نکردن که خب ...

من خودم این رو چک کردم ولی به گفته ی دوستان لزومی به چک کردنش نیست.

 

[A.Sina]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

این سوالارو نمیشه با استقرا اثبات کرد(اگه کسی هم با استقرا اثبات کرده باشه احتمالا این جوری حل کرده که به فرض استقرا 1 ترازو سنگین تر اضافه کنه و... که کاملا غلطه)
من تو کف سوال 3ام کسی تونسته کاریش بکنه؟ اصلا نمی فهمم چجوری باید از خاصیت نقطه ی n استفاده کرد.

شما فک کنم زیادی استقرا رو دست کم گرفتین

لزومی نداره که حتما روی n استقرا بزنیم

یه راه حل با استقرا میتونه این باشه:

بدون کاسته شدن از کلیت مسئله فرض کنین
w1<=w2<=w3<=...<=wn

فک کنم همتون قبول دارید که w1 یه مجموعه ی کامله چون میشه به راحتی ثابت کرد w1=1

میشه ثابت کرد به ازای هر i<=n-1 ،
w1+w2+w3+...+Wi>=Wi+1 -1
(w اندیس i+1 منهای یک)

چون اگه اینجوری نباشه عدد Wi+1 -1 رو نمیشه به صورت مجموع تعدادی از w ها نوشت که تناقضه

از این استفاده کنین ثابت کنین اگه w1,w2,...wi کامل باشه، w1,w2,....wi,wi+1 هم کامله

به این ترتیب ثابت میشه w1,w2,...,wn-1 هم کامله که همون حکم مسئله بود

یه راه حل نسبتا ساده با استقرا...

:89:

 

[fisa ghores]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

یعنی شما اصلا وقت ندارید که پاسخ سوالارو بذارید؟:41::41:

 

[ali.bsh]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

ای بابا.این چه وضعشه.پاسخنامه ی همه ی المپیاد ها رو زدن به جز ریاضی.کی می زنن پس؟

 

[ehsanir]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

dar soale 3 roze aval sabet mishe ke vasat kaman bac ham roye dayere akol ast
baghiye rah ham ba ya tashaboh va zaviye dar miyad
taze mishe soal ro tamim ham dad: mishe be jaye o har noghte dige roye amod monasef bc ke to dayere bashe ro ham dar nazar gereft
dar kol soale khoby bod
hala kasi az jam bandi in harfa nemitone bege ke kaf chande?

 

[A.Sina]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

به نظر میاد کف نزدیک 4 تا باشه شاید یکم کمتر مثلا 25

من که کلا ناامید شدم:20:

 

[mohy1376]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

شما فک کنم زیادی استقرا رو دست کم گرفتین

لزومی نداره که حتما روی n استقرا بزنیم

یه راه حل با استقرا میتونه این باشه:

بدون کاسته شدن از کلیت مسئله فرض کنین
w1<=w2<=w3<=...<=wn

فک کنم همتون قبول دارید که w1 یه مجموعه ی کامله چون میشه به راحتی ثابت کرد w1=1

میشه ثابت کرد به ازای هر i<=n-1 ،
w1+w2+w3+...+Wi>=Wi+1 -1
(w اندیس i+1 منهای یک)

چون اگه اینجوری نباشه عدد Wi+1 -1 رو نمیشه به صورت مجموع تعدادی از w ها نوشت که تناقضه

از این استفاده کنین ثابت کنین اگه w1,w2,...wi کامل باشه، w1,w2,....wi,wi+1 هم کامله

به این ترتیب ثابت میشه w1,w2,...,wn-1 هم کامله که همون حکم مسئله بود

یه راه حل نسبتا ساده با استقرا...

:89:

آفرین ، یه همچین راهی به نظرم رفتم.:41::41:

 

[ehsanir]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

bache haye dore team migan ke kaf dore 25
vali kheyli vaght ha kaf az pishbini ha 3-4 nomre kamtar mishe

 

[mohy1376]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

bache haye dore team migan ke kaf dore 25

پس قبول نمیشم.:20::20::20::20:


اینو بیخیال ، سوال 5 چه جوری حل میشه؟؟؟؟؟

 

[amirrezaeshraghi]

پاسخ : بررسی سوالات مرحله دوم المپیاد ریاضی- دوره 31- بهار 1392

Ye noktei,, man soale 6 sabet kardam donbale harjoor bashe a5<_5 Kasi nazari dare??? :d