پاسخ : ماراتن نظریه ی اعداد (سطح ممتاز)
اين سوال دومي كه گذاشتين رو من حل كردم:
اگه دو طرف رو به پيمانه ي 4 در نظر بگيريم به راحتي مي تونيم بدست بياريم
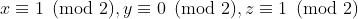 حالا دقت كنيد كه
حالا دقت كنيد كه
 نمي تونه به شكل
نمي تونه به شكل
 باشه چون در اين حالت داريم:
باشه چون در اين حالت داريم:
 پس
پس
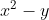 يه عامل اول مثل p داره كه به شكل
يه عامل اول مثل p داره كه به شكل
 هست كه اين نتيجه ميده:
هست كه اين نتيجه ميده:
 كه تناقضه پس
كه تناقضه پس
 به شكل
به شكل
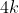 هست كه در اين صورت داريم:
هست كه در اين صورت داريم:
 كه تناقضه. پس معادله جواب صحيح نداره.
كه تناقضه. پس معادله جواب صحيح نداره.
---- دو نوشته به هم متصل شده است ----
سوال بعد:
تمام اعداد طبيعي
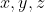 را بيابيد به طوريكه داشته باشيم
را بيابيد به طوريكه داشته باشيم

بلی!
داریم:
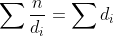 .پس اگه طرفین رو در n ضرب کنیم به
.پس اگه طرفین رو در n ضرب کنیم به
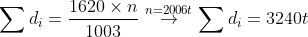 میرسیم.بعد چون سمت چپ طبیعیه سمت راست هم باید طبیعی باشه پس
میرسیم.بعد چون سمت چپ طبیعیه سمت راست هم باید طبیعی باشه پس
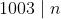 . حالا چون n زوجه
. حالا چون n زوجه
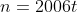 و ... .
و ... .
---- دو نوشته به هم متصل شده است ----
سوال بعد:ثابت کنید برای نامتناهی n،
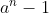 حداقل یک عامل اول بزرگتر از
حداقل یک عامل اول بزرگتر از
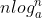 دارد.(a طبیعی و از 1 بزرگتر است.)
دارد.(a طبیعی و از 1 بزرگتر است.)
---- دو نوشته به هم متصل شده است ----
آقا من اول که این سوال رو حل کردم فکر کردم آسونه بعد یکم فکر کردم دیدم جوب زدم و یکم سخته.اگه راه آسونی پیدا کردید بگید.این یه سوال دیگه:
ثابت کنید معادله
 در اعداد صحیح جواب ندارد.
در اعداد صحیح جواب ندارد.
داریم:
---- دو نوشته به هم متصل شده است ----
سوال بعد:ثابت کنید برای نامتناهی n،
---- دو نوشته به هم متصل شده است ----
آقا من اول که این سوال رو حل کردم فکر کردم آسونه بعد یکم فکر کردم دیدم جوب زدم و یکم سخته.اگه راه آسونی پیدا کردید بگید.این یه سوال دیگه:
ثابت کنید معادله
اگه دو طرف رو به پيمانه ي 4 در نظر بگيريم به راحتي مي تونيم بدست بياريم
---- دو نوشته به هم متصل شده است ----
سوال بعد:
تمام اعداد طبيعي
آخرین ویرایش توسط مدیر
