من سه تا سوال قشنگ هندسه (البته به نظر خودم) ميذارم تا شما هم استفاده كنيد. اگه كسي از دوستان هم سوال قشنگي ديد خوشحال ميشم كه توي اين تاپيك اونو بذاره.
1- مثلث
 به راس
به راس
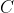 متساوي الساقين است. وسط
متساوي الساقين است. وسط
 را
را
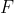 مي ناميم و نقطه ي
مي ناميم و نقطه ي
 را روي
را روي
 طوري در نظر مي گيريم كه
طوري در نظر مي گيريم كه
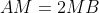 . اگر
. اگر
 پاي عمود وارد بر
پاي عمود وارد بر
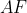 از
از
 باشد نشان دهيد
باشد نشان دهيد
 .
.
2- در متوازي الاضلاع
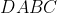 نقاط
نقاط
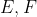 را به ترتيب روي
را به ترتيب روي
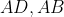 طوري انتخاب مي كنيم كه
طوري انتخاب مي كنيم كه
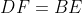 باشد. اگر
باشد. اگر
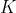 محل برخورد
محل برخورد
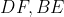 باشد نشان دهيد
باشد نشان دهيد
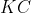 نيمساز زاويه ي
نيمساز زاويه ي
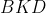 است.
است.
3- در مثلث
 ،
،
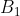 پاي نيمساز راس
پاي نيمساز راس
 و
و
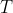 وسط كمان
وسط كمان
 از دايره ي محيطي اين مثلث (كماني كه شامل راس
از دايره ي محيطي اين مثلث (كماني كه شامل راس
 نيست) است. نقطه ي
نيست) است. نقطه ي
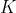 را روي دايره ي محيطي و نقطه ي
را روي دايره ي محيطي و نقطه ي
 را روي
را روي
 طوري در نظر مي گيريم كه
طوري در نظر مي گيريم كه
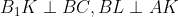 . نشان دهيد
. نشان دهيد
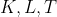 همخطند.
همخطند.
1- مثلث
2- در متوازي الاضلاع
3- در مثلث
