یه اثبات واسه دنباله حسابی
پاسخ : یه اثبات واسه دنباله حسابی
ممنون دوست عزیز
این طور که شما گفتی باهم خط نمی خورن که. ممنون میشم اگه روی کاغذ بنویسید بعد با گوشیتون عکس بگیریند بزارید یا اسکن کنید .
سپاس ...
وسطی منهای دست چپی میشه (c-a)(a+b+c) و دست راستی منهای وسطی میشه (a-b)(a+b+c) که با توجه به این که a,b,c تو تصاعد حسابی هستن, پس این دوتا عدد با هم برابرن, یعنی اون سه تا عدد اولی هم تو تصاعد حسابی هستن.
این طور که شما گفتی باهم خط نمی خورن که. ممنون میشم اگه روی کاغذ بنویسید بعد با گوشیتون عکس بگیریند بزارید یا اسکن کنید .
سپاس ...
پاسخ : یه اثبات واسه دنباله حسابی
آموزش نوشتن فرمول های ریاضی
http://www.irysc.com/files/other/equation-in-forum.swf
آموزش نوشتن فرمول های ریاضی
http://www.irysc.com/files/other/equation-in-forum.swf
- ارسال ها
- 65
- لایک ها
- 10
- امتیاز
- 0
پاسخ : یه اثبات واسه دنباله حسابی
فرض:

اتحاد چاق و لاغر:

پس در نتيجه حكم:

تشكيل دنباله ي حسابي مي دهند.
نوع اثبات:بازگشتي

پس اگر فرض مسئله
 ميبود سوال حل ميشد.به نظر من سوال بايد ميگفت:فرض كنيم
ميبود سوال حل ميشد.به نظر من سوال بايد ميگفت:فرض كنيم
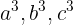 تشكيل يك تصاعد حسابي مي دهند.البته اگر
تشكيل يك تصاعد حسابي مي دهند.البته اگر
 باشد مشكلي پيش نمي آيد ولي وقتي
باشد مشكلي پيش نمي آيد ولي وقتي
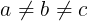 باشد همان كه گفتم.اميد وارم دوستان مرا راهنمايي كنند.
باشد همان كه گفتم.اميد وارم دوستان مرا راهنمايي كنند.
فرض:
اتحاد چاق و لاغر:
پس در نتيجه حكم:
تشكيل دنباله ي حسابي مي دهند.
نوع اثبات:بازگشتي
پس اگر فرض مسئله
پاسخ : یه اثبات واسه دنباله حسابی
میشه بگین کجاش مشکل داره و اصلا چه ربطی به این داره که اون سه تا عدد برابر باشن؟؟؟ من ثابت کردم اگه a,b,c تو یه تساعد حسابی با قدر نسبت d باشن, اون سه تا عدد هم تو یه تصاعد حسابی با قدر نسبت (d(a+b+c هستن. مشکلش چیه؟؟؟
اين راه حل وقتي صدق ميكنه كه a,b,cبا هم برابر باشند.در غير اين صورت فك نكنم جواب بده
لا اقل جمله ي آخرتون رو يه كم توضيح بدين
لا اقل جمله ي آخرتون رو يه كم توضيح بدين
- ارسال ها
- 65
- لایک ها
- 10
- امتیاز
- 0
پاسخ : یه اثبات واسه دنباله حسابی
گفته شده ثابت کنید اون سه تا عدد تو عکس تو تصاعد حسابی هستن, کجا گفته شده با همین ترتیب؟؟ اگه تو پستای صفحه قبل دقیق بشی می بینی خود کسی هم که سوالو گذاشته منظورش این بوده که اینا با یه ترتیب درستی تو تصاعد هستن.
ميفهمم چي ميگي ولي تو اينو ثابت كردي:
,(a^{2}+ac+c^{2}),(b^{2}+bc+c^{2}))
در حالي كه سوال اينو مي خواد:
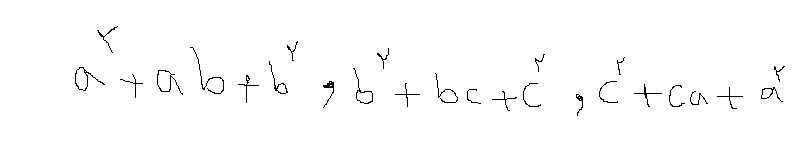
ااز اين به بعد زود قضاوت نكن!!!
در حالي كه سوال اينو مي خواد:
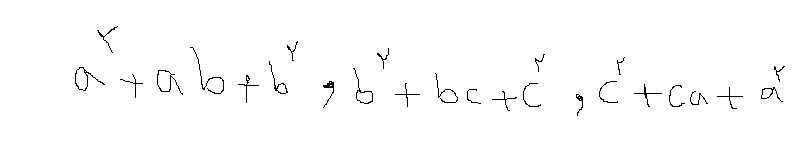
ااز اين به بعد زود قضاوت نكن!!!
- ارسال ها
- 65
- لایک ها
- 10
- امتیاز
- 0
پاسخ : یه اثبات واسه دنباله حسابی
اگه جاي دو جمله ي آخر(از سمت چپ)عوض بشه،همه چيز حله.
اما يه فكري رو اثبات من بكن ببين ميتونه درست باشه؟
ممنون...
گفته شده ثابت کنید اون سه تا عدد تو عکس تو تصاعد حسابی هستن, کجا گفته شده با همین ترتیب؟؟ اگه تو پستای صفحه قبل دقیق بشی می بینی خود کسی هم که سوالو گذاشته منظورش این بوده که اینا با یه ترتیب درستی تو تصاعد هستن.
اما يه فكري رو اثبات من بكن ببين ميتونه درست باشه؟
ممنون...
پاسخ : یه اثبات واسه دنباله حسابی
ببین عزیزم تو هنوز مشکلت اینه که فکر می کنی اون سه تا عدد گفته شده باید با همون ترتیب تو تصاعد باشن, واسه همین میگی: اگه جای دو جمله آخر (از سمت چپ) عوض بشه.....در صورتی که هیچ ترتیب خاصی روی اون سه تا عدد وجود نداره و این ماییم که باید تصمیم بگیریم چه ترتیبیو انتخاب کنیم. مثلا اینجا رو ببین: AoPS Forum - Nine point circle is tangent to incircle and three excircles • Art of Problem Solving تو صورت این سوال, گفته شده به ترتیب, در صورتی که اگر گفته نمی شد ما می تونستیم هر ترتیب دلخواهیو در نظر بگیریم, مثل اینجا که در مورد ترتیب اون سه تا عدد هیچ حرفی نزده. تو هم اگه تو راه حلت ترتیب درست رو در نظر بگیری قطعا درست میشه.
اگه جاي دو جمله ي آخر(از سمت چپ)عوض بشه،همه چيز حله.
اما يه فكري رو اثبات من بكن ببين ميتونه درست باشه؟
ممنون...
اما يه فكري رو اثبات من بكن ببين ميتونه درست باشه؟
ممنون...
- ارسال ها
- 65
- لایک ها
- 10
- امتیاز
- 0
پاسخ : یه اثبات واسه دنباله حسابی
نيازي به گفتن نيست.قرارداد اينه كه عبارت هاي ذكر شده از چپ به راست و به ترتيب تو دنباله باشن....به هر حال بي خيال
لازمه بدوني اين سوال از رياضي 2 مبتكران استخراج شده و من اونجا رو كه نيگا مي كردم مي ديدم صورتشو درست نوشته اما كاربرessann اشتباه كرده و راه حل شما (با اين شرايط و اوصاف).درسته
پس بهتر ميدونم كه هينجا پرونده ي ان مسئله ي به شدت آسون رو مختومه اعلا كنيم!!
موافقي؟؟
گفته شده ثابت کنید اون سه تا عدد تو عکس تو تصاعد حسابی هستن, کجا گفته شده با همین ترتیب؟؟ اگه تو پستای صفحه قبل دقیق بشی می بینی خود کسی هم که سوالو گذاشته منظورش این بوده که اینا با یه ترتیب درستی تو تصاعد هستن.
لازمه بدوني اين سوال از رياضي 2 مبتكران استخراج شده و من اونجا رو كه نيگا مي كردم مي ديدم صورتشو درست نوشته اما كاربرessann اشتباه كرده و راه حل شما (با اين شرايط و اوصاف).درسته
پس بهتر ميدونم كه هينجا پرونده ي ان مسئله ي به شدت آسون رو مختومه اعلا كنيم!!
موافقي؟؟
پاسخ : یه اثبات واسه دنباله حسابی
من حرفی ندارم, بحثی بود که خودت شروعش کردی, ولی اینو بدون که یه همچین قراردادی که میگی اصلا وجود نداره. تا ترتیب ذکر نشه هیچ ترتیبی روی چند تا چیزی که هستن وجود نداره, مثل یه مجموعه. اگه حرف منو قبول نداری میتونی از راهبران یا مشاورین یا کاربرایی مثل mahanmath,bgo,astronomer1 که امسال طلا گرفتن بپرسی که حرفشون معتبره. هرچی اونا بگن من قبول دارم.
نيازي به گفتن نيست.قرارداد اينه كه عبارت هاي ذكر شده از چپ به راست و به ترتيب تو دنباله باشن....به هر حال بي خيال
لازمه بدوني اين سوال از رياضي 2 مبتكران استخراج شده و من اونجا رو كه نيگا مي كردم مي ديدم صورتشو درست نوشته اما كاربرessann اشتباه كرده و راه حل شما (با اين شرايط و اوصاف).درسته
پس بهتر ميدونم كه هينجا پرونده ي ان مسئله ي به شدت آسون رو مختومه اعلا كنيم!!
موافقي؟؟
لازمه بدوني اين سوال از رياضي 2 مبتكران استخراج شده و من اونجا رو كه نيگا مي كردم مي ديدم صورتشو درست نوشته اما كاربرessann اشتباه كرده و راه حل شما (با اين شرايط و اوصاف).درسته
پس بهتر ميدونم كه هينجا پرونده ي ان مسئله ي به شدت آسون رو مختومه اعلا كنيم!!
موافقي؟؟
