ماراتن سوالات تستی مرحله دوم المپیاد کامپیوتر
پاسخ : ماراتن سوالات تستی مرحله دوم المپیاد کامپیوتر
خب منظور این دوستمون اینه که جمع مهره های جدول ثابته!
یه راه دیگه اونم همین شکلی هست که به هر خونه یه مختصات بدیم
مجموع طول و عرض مختصات ثابته
حالا راه من (فکر کنم قشنگه)
چون میتوان فرض کرد همه گلوله ها یکسان اند مرکز ثقل مجمو گلوله ها ثابت است(اون وسط میفته مرکز ثقل)
خونه های جدول رو از بالا و سمت چپ به تریب با اعداد 1 تا 16 شماره گذاری میکنیم !!! حالا ناوردمون این میشه :
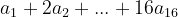 (
(
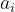 تعداد مهره های خانه با شماره ی
تعداد مهره های خانه با شماره ی
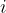 هست) ....... بقیشم بدیهیه
هست) ....... بقیشم بدیهیه 
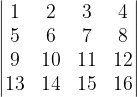
یه راه دیگه اونم همین شکلی هست که به هر خونه یه مختصات بدیم
مجموع طول و عرض مختصات ثابته
حالا راه من (فکر کنم قشنگه)
چون میتوان فرض کرد همه گلوله ها یکسان اند مرکز ثقل مجمو گلوله ها ثابت است(اون وسط میفته مرکز ثقل)
آخرین ویرایش توسط مدیر
پاسخ : ماراتن سوالات تستی مرحله دوم المپیاد کامپیوتر
سوال 11 :

http://webl.host56.com/photos/7de931935327.gif
سوال 11 :

http://webl.host56.com/photos/7de931935327.gif
پاسخ : ماراتن سوالات تستی مرحله دوم المپیاد کامپیوتر
این سوال هم هیچی، ولی دقت کنید، اسم این تاپیک هست ماراتون سوالات تستی. نه تشریحی. ولی الآن سوالای تشریحی داریم می زاریم. این سوالا رو ، تو تاپیک های مربوطه بزارید.
پاسخ: استقرا می زنیم روی یال ها. یه راس رو در نظر می گیریم و فرض می کنیم که input از output کمتر مساوی باشه. حالا همه input ها را حذف می کنیم.( جزو حذفی ها می گذاریم ) یال های output هم نمی تونند توی دوری باشند. ( بدیهی است ) حالا برای این که از فرضمون استفاده کنیم اون یال ها را هم حذف می کنیم ( یعنی اون راس را حذف می کنیم ) و حل میشه.
سوال تستی م دو سال قبل
جوابش هم میشه 51
(عذر خواهی میکنم که کامل نگفتم )!!
سوال 12
ثابت کنید از یک گراف جهت دار میتوان حداکثر نصف یالها رو حذف کرد و دیگر دوری وجود نداشته باشد
جوابش هم میشه 51
(عذر خواهی میکنم که کامل نگفتم )!!
سوال 12
ثابت کنید از یک گراف جهت دار میتوان حداکثر نصف یالها رو حذف کرد و دیگر دوری وجود نداشته باشد
پاسخ: استقرا می زنیم روی یال ها. یه راس رو در نظر می گیریم و فرض می کنیم که input از output کمتر مساوی باشه. حالا همه input ها را حذف می کنیم.( جزو حذفی ها می گذاریم ) یال های output هم نمی تونند توی دوری باشند. ( بدیهی است ) حالا برای این که از فرضمون استفاده کنیم اون یال ها را هم حذف می کنیم ( یعنی اون راس را حذف می کنیم ) و حل میشه.
آخرین ویرایش توسط مدیر
پاسخ : ماراتن سوالات تستی مرحله دوم المپیاد کامپیوتر
بیاید اینم سوالش حداقل چند یال رو حذف کنیم که اون شرطه برقرارشه
الف q/2
ب q/3
ج 2q/3
دهیچکدام
منم راهی برای این سواله بگم !تقریبا(شایدم دقیقا)همونیه که دوستمون گفته!
میتونیم همه راس ها رو رو یک خط بگذاریم یالی که از یک راس به راسی که روی خط قبل از آن هست میرود اززیر خط رسم شود و یالهایی که به رئوس بعد میرود از بالای خط رسم میکنیم! خب یک گروه از یالها زیر یا رو کمتر مساوی نصف یالهاست آن گروه رو حذف میکنیم
سوال بعدی رو خودت بگو hoco.hcجان
این سوال هم هیچی، ولی دقت کنید، اسم این تاپیک هست ماراتون سوالات تستی. نه تشریحی. ولی الآن سوالای تشریحی داریم می زاریم. این سوالا رو ، تو تاپیک های مربوطه بزارید.
پاسخ: استقرا می زنیم روی یال ها. یه راس رو در نظر می گیریم و فرض می کنیم که input از output کمتر مساوی باشه. حالا همه input ها را حذف می کنیم.( جزو حذفی ها می گذاریم ) یال های output هم نمی تونند توی دوری باشند. ( بدیهی است ) حالا برای این که از فرضمون استفاده کنیم اون یال ها را هم حذف می کنیم ( یعنی اون راس را حذف می کنیم ) و حل میشه.
پاسخ: استقرا می زنیم روی یال ها. یه راس رو در نظر می گیریم و فرض می کنیم که input از output کمتر مساوی باشه. حالا همه input ها را حذف می کنیم.( جزو حذفی ها می گذاریم ) یال های output هم نمی تونند توی دوری باشند. ( بدیهی است ) حالا برای این که از فرضمون استفاده کنیم اون یال ها را هم حذف می کنیم ( یعنی اون راس را حذف می کنیم ) و حل میشه.
الف q/2
ب q/3
ج 2q/3
دهیچکدام
منم راهی برای این سواله بگم !تقریبا(شایدم دقیقا)همونیه که دوستمون گفته!
میتونیم همه راس ها رو رو یک خط بگذاریم یالی که از یک راس به راسی که روی خط قبل از آن هست میرود اززیر خط رسم شود و یالهایی که به رئوس بعد میرود از بالای خط رسم میکنیم! خب یک گروه از یالها زیر یا رو کمتر مساوی نصف یالهاست آن گروه رو حذف میکنیم
سوال بعدی رو خودت بگو hoco.hcجان
پاسخ : ماراتن سوالات تستی مرحله دوم المپیاد کامپیوتر
این در حقیقت تقریبا مثل ایده قشنگ ترتیب توپولوژیک بود. ( توی الگوریتم و برنامه نویسی ، البته اون نبودا، ولی یه جورایی پیاده سازیش مثل این بود )
سوال بعدی:
چند زیر مجموعه 5 عضوی از 18 عدد اوّل طبیعی می توان یافت ، به طوری که هر دو عضوی از این مجموعه ها تفاضلشان حداقل 2 باشد.
( حالت را برای تفاضل 3 نیز حل کنید )
بیاید اینم سوالش حداقل چند یال رو حذف کنیم که اون شرطه برقرارشه
الف q/2
ب q/3
ج 2q/3
دهیچکدام
منم راهی برای این سواله بگم !تقریبا(شایدم دقیقا)همونیه که دوستمون گفته!
میتونیم همه راس ها رو رو یک خط بگذاریم یالی که از یک راس به راسی که روی خط قبل از آن هست میرود اززیر خط رسم شود و یالهایی که به رئوس بعد میرود از بالای خط رسم میکنیم! خب یک گروه از یالها زیر یا رو کمتر مساوی نصف یالهاست آن گروه رو حذف میکنیم
سوال بعدی رو خودت بگو hoco.hcجان
الف q/2
ب q/3
ج 2q/3
دهیچکدام
منم راهی برای این سواله بگم !تقریبا(شایدم دقیقا)همونیه که دوستمون گفته!
میتونیم همه راس ها رو رو یک خط بگذاریم یالی که از یک راس به راسی که روی خط قبل از آن هست میرود اززیر خط رسم شود و یالهایی که به رئوس بعد میرود از بالای خط رسم میکنیم! خب یک گروه از یالها زیر یا رو کمتر مساوی نصف یالهاست آن گروه رو حذف میکنیم
سوال بعدی رو خودت بگو hoco.hcجان
سوال بعدی:
چند زیر مجموعه 5 عضوی از 18 عدد اوّل طبیعی می توان یافت ، به طوری که هر دو عضوی از این مجموعه ها تفاضلشان حداقل 2 باشد.
( حالت را برای تفاضل 3 نیز حل کنید )
پاسخ : ماراتن سوالات تستی مرحله دوم المپیاد کامپیوتر
این سوال با تناظر یک به یک حل می شه ، رجوع شود به الفبا صفحه 72 !
سوال 14 :
3 عدد بعدی دنباله ی زیر چیست؟
الگوریتمی برای بدست آوردن مجموع ارقام و تعداد ارقام n اُمین عدد ارائه کنید.
1,11,21,1211,111221,312211,...
سوال بعدی:
چند زیر مجموعه 5 عضوی از 18 عدد اوّل طبیعی می توان یافت ، به طوری که هر دو عضوی از این مجموعه ها تفاضلشان حداقل 2 باشد.
( حالت را برای تفاضل 3 نیز حل کنید )
چند زیر مجموعه 5 عضوی از 18 عدد اوّل طبیعی می توان یافت ، به طوری که هر دو عضوی از این مجموعه ها تفاضلشان حداقل 2 باشد.
( حالت را برای تفاضل 3 نیز حل کنید )
سوال 14 :
3 عدد بعدی دنباله ی زیر چیست؟
الگوریتمی برای بدست آوردن مجموع ارقام و تعداد ارقام n اُمین عدد ارائه کنید.
1,11,21,1211,111221,312211,...
آخرین ویرایش توسط مدیر
