مسابقه ریاضی ((حل کنید !))
پاسخ : مسابقه ریاضی ((حل کنید !))

تساوی اول و نامساوی آخر(مربعی-حسابی) واضحند.
برای اثبات اولین نامساوی: (اثبات هندسی)
مستطیل های
 را با رأس های
را با رأس های
 (i=1,2,...,n) در نظر بگیرید. مساحت مستطیل k ام برابر است با
(i=1,2,...,n) در نظر بگیرید. مساحت مستطیل k ام برابر است با
 . پس مجموع مساحت های این مستطیل های دو به دو جدا از هم برابر است با طرف چپ نامساوی.
. پس مجموع مساحت های این مستطیل های دو به دو جدا از هم برابر است با طرف چپ نامساوی.
مستطیل های
 را با رأس های
را با رأس های
 (i=1,2,...,n) در نظر بگیرید. مساحت مستطیل k ام برابر است با
(i=1,2,...,n) در نظر بگیرید. مساحت مستطیل k ام برابر است با
 . پس مجموع مساحت های این مستطیل های دو به دو جدا از هم برابر است با طرف راست نامساوی.
. پس مجموع مساحت های این مستطیل های دو به دو جدا از هم برابر است با طرف راست نامساوی.
حالا کافیه ثابت کنید مستطیل های
 مستطیل های
مستطیل های
 رو میپوشونن... که اگر شکلش رو بکشید ایده ی اثبات این قسمت خیلی راحت به ذهن میرسه.
رو میپوشونن... که اگر شکلش رو بکشید ایده ی اثبات این قسمت خیلی راحت به ذهن میرسه.
می دانیم که :

و
 دنباله ای از اعداد حقیقی است.
دنباله ای از اعداد حقیقی است.
ثابت کنید که :

و
ثابت کنید که :
دنبال یه روش بهترم
برای اثبات اولین نامساوی: (اثبات هندسی)
مستطیل های
مستطیل های
حالا کافیه ثابت کنید مستطیل های
- ارسال ها
- 107
- لایک ها
- 53
- امتیاز
- 0
پاسخ : مسابقه ریاضی ((حل کنید !))
نه آقای شریفی شرط
=f(x)^2) تو صورت سوال نیست .
تو صورت سوال نیست .
Russia All-Russian Olympiad 2005 • Art of Problem Solving
ولی کراندار رو دقت نکردم پس اثباتم غلطه. :93::93:
آیا تابع کران دار
) وجود دارد به طوری که :
وجود دارد به طوری که :

>&space;0)
\geq&space;f^{2}(x)+2f(xy)+f^{2}(y))
* توجه کنید که
=f(x)^2) .
.
Russia All-Russian Olympiad 2005 • Art of Problem Solving
ولی کراندار رو دقت نکردم پس اثباتم غلطه. :93::93:
- ارسال ها
- 107
- لایک ها
- 53
- امتیاز
- 0
پاسخ : مسابقه ریاضی ((حل کنید !))
ببخشید اشتباه شد اون دو تا عبارت با هم برابر است. یه لحظه فکر کردم توان طرف راست داخل پرانتزه :93:
نه آقای شریفی شرط
=f(x)^2) تو صورت سوال نیست .
تو صورت سوال نیست .
Russia All-Russian Olympiad 2005 • Art of Problem Solving
ولی کراندار رو دقت نکردم پس اثباتم غلطه. :93::93:
Russia All-Russian Olympiad 2005 • Art of Problem Solving
ولی کراندار رو دقت نکردم پس اثباتم غلطه. :93::93:
پاسخ : مسابقه ریاضی ((حل کنید !))
سوال و جواب:
ثابت کنید:

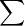
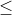

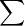
راه حل:
سوال و جواب:
ثابت کنید:
راه حل:
(اثبات هندسی)
مستطیل های
 را با رأس های
را با رأس های
 (i=1,2,...,n) در نظر بگیرید. مساحت مستطیل k ام برابر است با
(i=1,2,...,n) در نظر بگیرید. مساحت مستطیل k ام برابر است با
 . پس مجموع مساحت های این مستطیل های دو به دو جدا از هم برابر است با طرف چپ نامساوی.
. پس مجموع مساحت های این مستطیل های دو به دو جدا از هم برابر است با طرف چپ نامساوی.
مستطیل های
 را با رأس های
را با رأس های
 (i=1,2,...,n) در نظر بگیرید. مساحت مستطیل k ام برابر است با
(i=1,2,...,n) در نظر بگیرید. مساحت مستطیل k ام برابر است با
 . پس مجموع مساحت های این مستطیل های دو به دو جدا از هم برابر است با طرف راست نامساوی.
. پس مجموع مساحت های این مستطیل های دو به دو جدا از هم برابر است با طرف راست نامساوی.
حالا کافیه ثابت کنید مستطیل های
 مستطیل های
مستطیل های
 رو میپوشونن... که اگر شکلش رو بکشید ایده ی اثبات این قسمت خیلی راحت به ذهن میرسه.
رو میپوشونن... که اگر شکلش رو بکشید ایده ی اثبات این قسمت خیلی راحت به ذهن میرسه.
مستطیل های
مستطیل های
حالا کافیه ثابت کنید مستطیل های
پاسخ : مسابقه ریاضی ((حل کنید !))
\\=\sum_{k=1}^{n}{(\sqrt{k}-\sqrt{k-1})\sqrt{a_k}}\\\geq&space;\frac{1}{\sqrt{n}}\sum_{k=1}^{n}{\sqrt{a_k}}\geq&space;\sqrt{\sum_{k=1}^{n}{a_k}})
تساوی اول و نامساوی آخر(مربعی-حسابی) واضحند.
برای اثبات اولین نامساوی: (اثبات هندسی)
مستطیل های
 را با رأس های
را با رأس های
,(\sqrt{i},0),(\sqrt{i-1},\sqrt{a_i}),(\sqrt{i},\sqrt{a_i})) (i=1,2,...,n) در نظر بگیرید. مساحت مستطیل k ام برابر است با
(i=1,2,...,n) در نظر بگیرید. مساحت مستطیل k ام برابر است با
\sqrt{a_k}) . پس مجموع مساحت های این مستطیل های دو به دو جدا از هم برابر است با طرف چپ نامساوی.
. پس مجموع مساحت های این مستطیل های دو به دو جدا از هم برابر است با طرف چپ نامساوی.
مستطیل های
 را با رأس های
را با رأس های
,(\frac{i}{\sqrt{n}},0),(\frac{i-1}{\sqrt{n}},\sqrt{a_i}),(\frac{i}{\sqrt{n}},\sqrt{a_i})) (i=1,2,...,n) در نظر بگیرید. مساحت مستطیل k ام برابر است با
(i=1,2,...,n) در نظر بگیرید. مساحت مستطیل k ام برابر است با
) . پس مجموع مساحت های این مستطیل های دو به دو جدا از هم برابر است با طرف راست نامساوی.
. پس مجموع مساحت های این مستطیل های دو به دو جدا از هم برابر است با طرف راست نامساوی.
حالا کافیه ثابت کنید مستطیل های
 مستطیل های
مستطیل های
 رو میپوشونن... که اگر شکلش رو بکشید ایده ی اثبات این قسمت خیلی راحت به ذهن میرسه.
با این ایده معروف این مسئله رو هم حل کنید :
رو میپوشونن... که اگر شکلش رو بکشید ایده ی اثبات این قسمت خیلی راحت به ذهن میرسه.
با این ایده معروف این مسئله رو هم حل کنید :
AoPS Forum - Problem 5, Iberoamerican Olympiad 2011 • Art of Problem Solving
یه مسئله تورنمت هم هست که اینطوری حل میشه ولی دقیق صورتش یادم نیست :71:
برای اثبات اولین نامساوی: (اثبات هندسی)
مستطیل های
مستطیل های
حالا کافیه ثابت کنید مستطیل های
AoPS Forum - Problem 5, Iberoamerican Olympiad 2011 • Art of Problem Solving
یه مسئله تورنمت هم هست که اینطوری حل میشه ولی دقیق صورتش یادم نیست :71:
پاسخ : مسابقه ریاضی ((حل کنید !))
چند تا سوال !؟
من که اثباتش کردم دیگه چرا این همه پست می زنید ؟
چرا zz_torna2 بجای hkh74 پست زدند ؟
چرا POURIYA_F به آقای شریفی جواب دادن ؟؟؟ ایشون که اصلا پست نزدن!
بسیار عالی بود، حالا من راه خودمو میگذارم : ( خودم که نه ! )
^2)
یه جورایی شبیه روش تغییر متغیره !
=\sum_{k=1}^{n}kx_{k}^{2}+2\sum_{1\leq i< j\leq n}ix_ix_j\leq \sum_{k=1}^{n}kx_{k}^{2}+2\sum_{1\leq i< j\leq n}\sqrt{ij}x_ix_j=(\sum_{k=1}^{n}\sqrt{k}x_k)^2.)
و حالا کافیه از دو طرف جذر بگیریم.
حالا یکی باید یه سوال بگذاره ، در ضمن به جناب hkh74 و alich100 هم امتیاز اضافه میشه.
یه جورایی شبیه روش تغییر متغیره !
و حالا کافیه از دو طرف جذر بگیریم.
حالا یکی باید یه سوال بگذاره ، در ضمن به جناب hkh74 و alich100 هم امتیاز اضافه میشه.
من که اثباتش کردم دیگه چرا این همه پست می زنید ؟
چرا zz_torna2 بجای hkh74 پست زدند ؟
راست میگیا حواسم نبود اثبات گفته تون:
پاسخ : مسابقه ریاضی ((حل کنید !))
چند تا سوال !؟
من که اثباتش کردم دیگه چرا این همه پست می زنید ؟
چرا zz_torna2 بجای hkh74 پست زدند ؟
چرا POURIYA_F به آقای شریفی جواب دادن ؟؟؟ ایشون که اصلا پست نزدن!
آقای یوسفی1
بهت قول میدم کارآگاه خوبی خواهی شد! سوالات خوبی میپرسی برای رسیدن به سرنخ!
سوال 1- فکر کنم جناب تورنا می خواستند سوال و جواب رو یه دفعه توی یه پست بذارن که بچه ها استفاده کنند.
سوال 2- اگه دقت کرده باشی آقای شریفی پست پوریا خان رو ویرایش کرده بودند که اقا پوریا هم یه پست خطاب به استاد زدند!
ولی من پلیس بهتری میشم قطعا!!
چند تا سوال !؟
من که اثباتش کردم دیگه چرا این همه پست می زنید ؟
چرا zz_torna2 بجای hkh74 پست زدند ؟
چرا POURIYA_F به آقای شریفی جواب دادن ؟؟؟ ایشون که اصلا پست نزدن!
بهت قول میدم کارآگاه خوبی خواهی شد! سوالات خوبی میپرسی برای رسیدن به سرنخ!
سوال 1- فکر کنم جناب تورنا می خواستند سوال و جواب رو یه دفعه توی یه پست بذارن که بچه ها استفاده کنند.
سوال 2- اگه دقت کرده باشی آقای شریفی پست پوریا خان رو ویرایش کرده بودند که اقا پوریا هم یه پست خطاب به استاد زدند!
ولی من پلیس بهتری میشم قطعا!!
