مسابقه ریاضی ((حل کنید !))
پاسخ : مسابقه ریاضی ((حل کنید !))
سوال اینه:
تعداد نقاط با مختصاتx و y صحیح داخل اون نه مساحت
سوال:
مساحتش میشه

یه مربع در نظر میگیریم بعد 4 تا ربع دایره رو از توش کم می کنیم.
اگه فاکتور بگیریم میشه :
r^2)
یه مربع در نظر میگیریم بعد 4 تا ربع دایره رو از توش کم می کنیم.
اگه فاکتور بگیریم میشه :
تعداد نقاط با مختصاتx و y صحیح داخل اون نه مساحت
سوال:
سوال بعد(فعلا از سوال آقای پوریا صرف نظر می کنیم)
تعداد نقاط صحیح داخل هاشور این شکل را حساب کنید:
دایره ها با هم برابر و شعاع آنها r است و بر محور ها مماسند
سوال نسبتا ساده ایست هر کی اینو حل کرد باید سوال بذاره!!!

تعداد نقاط صحیح داخل هاشور این شکل را حساب کنید:
دایره ها با هم برابر و شعاع آنها r است و بر محور ها مماسند
سوال نسبتا ساده ایست هر کی اینو حل کرد باید سوال بذاره!!!

آخرین ویرایش توسط مدیر
پاسخ : مسابقه ریاضی ((حل کنید !))
خب مسئله گاوس رو که میشه :

و با توجه به این شکل :
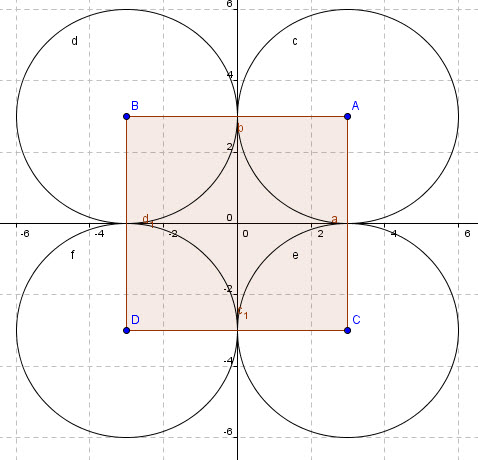
میدونیم که تعداد نقاط درون مربع میشه :

و اون چهار تا ربع دایره هم که تعداد نقاطشون میشه همون اندازه یه دایره که میشه :

حالا اگه دایره رو از مربع کم کنیم میشه اون قسمت رنگی :
)
ویرایش : " یادم رفت تهش
 رو بنویسم"
رو بنویسم"
خب مسئله گاوس رو که میشه :

و با توجه به این شکل :

میدونیم که تعداد نقاط درون مربع میشه :
و اون چهار تا ربع دایره هم که تعداد نقاطشون میشه همون اندازه یه دایره که میشه :

حالا اگه دایره رو از مربع کم کنیم میشه اون قسمت رنگی :
ویرایش : " یادم رفت تهش
آخرین ویرایش توسط مدیر
پاسخ : مسابقه ریاضی ((حل کنید !))
آقا چی شد؟
کسی حل نکرد
راهنمایی برای تعمیم مسئله گاوس (در ویکی هست):
3 حالت را بررسی کنید مختصه های مرکز هردو صحیح اند هیچکدوم صحیح نیستند و یکی صحیح است و دیگری صحیح نیست
فرض کنید مرکز
 باشد ما حالتی را حساب می کنیم که هیچکدوم صحیح نیستند (این حالت سختترین است)
باشد ما حالتی را حساب می کنیم که هیچکدوم صحیح نیستند (این حالت سختترین است)
باید x و y های صحیحی بیابیم که در این نامعادله صدق می کنند:

خب ما جواب را برای یک ربع حساب می کنیم مثلا ربع بالا راست و سپس ضربدر 4 می کنیم دقت کنید که a و b صحیح نیستند
پس داریم:

حال x را عدد به عدد امتحان می کنیم و تعداد y ها را با هم جمع می کنیم
یعنی :



.
.
.

پس تعداد y ها برابر همان هاست
یعنی :

پس

دیگه فک کنم سوالم بسیار ساده شد:
آقا چی شد؟
کسی حل نکرد
راهنمایی برای تعمیم مسئله گاوس (در ویکی هست):
3 حالت را بررسی کنید مختصه های مرکز هردو صحیح اند هیچکدوم صحیح نیستند و یکی صحیح است و دیگری صحیح نیست
فرض کنید مرکز
باید x و y های صحیحی بیابیم که در این نامعادله صدق می کنند:
خب ما جواب را برای یک ربع حساب می کنیم مثلا ربع بالا راست و سپس ضربدر 4 می کنیم دقت کنید که a و b صحیح نیستند
پس داریم:
حال x را عدد به عدد امتحان می کنیم و تعداد y ها را با هم جمع می کنیم
یعنی :
.
.
.
پس تعداد y ها برابر همان هاست
یعنی :
پس
دیگه فک کنم سوالم بسیار ساده شد:
تعداد نقاط با مختصات صحیح داخل هاشور این شکل را حساب کنید:
دایره ها با هم برابر و شعاع آنها r است و بر محور ها مماسند
سوال نسبتا ساده ایست هر کی اینو حل کرد باید سوال بذاره!!!

دایره ها با هم برابر و شعاع آنها r است و بر محور ها مماسند
سوال نسبتا ساده ایست هر کی اینو حل کرد باید سوال بذاره!!!

پاسخ : مسابقه ریاضی ((حل کنید !))
آقای alich100 ، من سوادم به این حرفا نمیرسه، خودت حل کن خیال ما رو راحت کن :45:
تا یه سوال راحت بذارم، همه حال بیان !
در ضمن طبق قوانینی که توی اولین پست این تاپیک وضع شده ، اگه یه سوال بیش از یک هفته خاک بخوره، خود طراح سوال باید جواب بده و از همه 1 امتیاز کسر میشه :دی
آقای alich100 ، من سوادم به این حرفا نمیرسه، خودت حل کن خیال ما رو راحت کن :45:
تا یه سوال راحت بذارم، همه حال بیان !
در ضمن طبق قوانینی که توی اولین پست این تاپیک وضع شده ، اگه یه سوال بیش از یک هفته خاک بخوره، خود طراح سوال باید جواب بده و از همه 1 امتیاز کسر میشه :دی
پاسخ : مسابقه ریاضی ((حل کنید !))
ععععععععععع چه قدر راه حل !!!!!! :4:اگر همین طوری استقبال بشه میشه سوالات open هم مطرح کنیم با این همه پیگری بالاخره حل میشه :4:
من یک راه حل میذارم اما راه حل های بیشتری هم داره
داریم

اگر
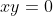 باشد مساله درست است
باشد مساله درست است
پس فرض میکنیم
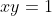
پس

حالا باید مینیمم
 را در
را در
 پیدا کنیم
پیدا کنیم
صعودی است
 پس
پس
 برای
برای
 که درست بودنش هم بدیهیه!!!!!
که درست بودنش هم بدیهیه!!!!!
من یک راه حل میذارم اما راه حل های بیشتری هم داره
داریم

اگر
پس فرض میکنیم
پس

حالا باید مینیمم


صعودی است



پاسخ : مسابقه ریاضی ((حل کنید !))
خب اخه خیلی ساده اس ادم حیفش میاد برا این سوال تایپ کنهشما که دست به مسیله ات خوبه چند تا ترکیبیات و گراف بزار جیگرمون حال بیاد
حالا سوال بعدی رو من می پرسم :چند عدد بین 100 تا 400 وجود داره که بر 3 بخش پذیر باشد و بر 7 بخش پذیر نباشد یا بر 7 بخش پذیر باشد و بر 3 بخش پذیر نباشد؟ "نگید سوال خیلی سادست، اینو گذاشتم که خاک نخوره :دی"
- ارسال ها
- 12
- لایک ها
- 36
- امتیاز
- 0
پاسخ : مسابقه ریاضی ((حل کنید !))
حالا که سوال قبلی جواب داده شد یک سوال قشنگ تر:
ثابت کنید بر روی هر خم بسته یک متوازی الاضاع داریم!
(نکته : خم بسته به طور خودمونی یعنی شکلی که بدون برداشتن مداد کشیده می شه و بسته است (مفهوم شکل باز وبسته برای اول ابتدایه!))
مثلا شکل زیر رو ببینید:
http://cli.comlu.com/photos/8ea2e8463760.jpg
حالا که سوال قبلی جواب داده شد یک سوال قشنگ تر:
ثابت کنید بر روی هر خم بسته یک متوازی الاضاع داریم!
(نکته : خم بسته به طور خودمونی یعنی شکلی که بدون برداشتن مداد کشیده می شه و بسته است (مفهوم شکل باز وبسته برای اول ابتدایه!))
مثلا شکل زیر رو ببینید:
http://cli.comlu.com/photos/8ea2e8463760.jpg
پاسخ : مسابقه ریاضی ((حل کنید !))
من اگر جوب نزده باشم (البته همیشه میزنم):4: با قضیه مینکوفسکی بشه یک مشبکه درست کنید و....
در ضمن توی سوال قبل هم گذاشتم اول گفتم با مشتق و تابع صعودی و ... نرید بعد دیدم را حل تابع صعودیش خیلی قشنگ تر از بقیه راه حل هاشه برای همین گفتم خودم بذارم که زیر حرفم هم نزده باشم:4:
این هم یک راه حل دیگه برای سوال قبل :
فرض کنید

پس داریم

میدانیم

پس

حالا که سوال قبلی جواب داده شد یک سوال قشنگ تر:
ثابت کنید بر روی هر خم بسته یک متوازی الاضاع داریم!
(نکته : خم بسته به طور خودمونی یعنی شکلی که بدون برداشتن مداد کشیده می شه و بسته است (مفهوم شکل باز وبسته برای اول ابتدایه!))
مثلا شکل زیر رو ببینید:
http://cli.comlu.com/photos/8ea2e8463760.jpg
ثابت کنید بر روی هر خم بسته یک متوازی الاضاع داریم!
(نکته : خم بسته به طور خودمونی یعنی شکلی که بدون برداشتن مداد کشیده می شه و بسته است (مفهوم شکل باز وبسته برای اول ابتدایه!))
مثلا شکل زیر رو ببینید:
http://cli.comlu.com/photos/8ea2e8463760.jpg
در ضمن توی سوال قبل هم گذاشتم اول گفتم با مشتق و تابع صعودی و ... نرید بعد دیدم را حل تابع صعودیش خیلی قشنگ تر از بقیه راه حل هاشه برای همین گفتم خودم بذارم که زیر حرفم هم نزده باشم:4:
این هم یک راه حل دیگه برای سوال قبل :
فرض کنید

پس داریم

میدانیم

پس

پاسخ : مسابقه ریاضی ((حل کنید !))
سوال قبل هم گذاشتم اول گفتم با مشتق و تابع صعودی و ... نرید بعد دیدم را حل تابع صعودیش خیلی قشنگ تر از بقیه راه حل هاشه برای همین گفتم خودم بذارم که زیر حرفم هم نزده باشم:4:
این هم یک راه حل دیگه برای سوال قبل :
فرض کنید

پس داریم

میدانیم

پس

این دیگه چه راه حلیه من یه راه حل سالم میذارم!!!
داریم:

که بدیهیه چون m^2k بین 0 و 1 است!
راستی خودت قبل از ویرایش نوشته بودی از راه تابع صعودی و مشتق و .. نرید بعد تابع صعودیشو پاک کردی خودت از اون راه رفتی؟@!!!!!!!!!!!!!!!
داریم:
که بدیهیه چون m^2k بین 0 و 1 است!
راستی خودت قبل از ویرایش نوشته بودی از راه تابع صعودی و مشتق و .. نرید بعد تابع صعودیشو پاک کردی خودت از اون راه رفتی؟@!!!!!!!!!!!!!!!
این هم یک راه حل دیگه برای سوال قبل :
فرض کنید

پس داریم

میدانیم

پس




